Klub 44M - zadania I 2013»Zadanie 653
o zadaniu...
- Zadanie pochodzi z artykułu Klub 44M - zadania I 2013
- Publikacja w Delcie: styczeń 2013
- Publikacja elektroniczna: 1 stycznia 2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (72 KB)
W egzaminie testowym pytania są ponumerowane
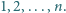 Za prawidłową
odpowiedź na
Za prawidłową
odpowiedź na
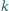 -te pytanie uczestnik otrzymuje
-te pytanie uczestnik otrzymuje
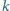 punktów; za
błędną (lub brak odpowiedzi) otrzymuje
punktów; za
błędną (lub brak odpowiedzi) otrzymuje
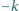 punktów. Po zliczeniu
wyników okazało się, że w każdej trójce uczestników znajdują się dwaj
tacy, którzy uzyskali różne sumy punktów. Jaka jest największa liczba
uczestników, dla której taka sytuacja mogła mieć miejsce?
punktów. Po zliczeniu
wyników okazało się, że w każdej trójce uczestników znajdują się dwaj
tacy, którzy uzyskali różne sumy punktów. Jaka jest największa liczba
uczestników, dla której taka sytuacja mogła mieć miejsce?
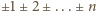 (dowolny układ znaków). Wszystkie takie liczby są jednakowej parzystości.
Zatem zbiór możliwych wyników zawiera się w zbiorze
(dowolny układ znaków). Wszystkie takie liczby są jednakowej parzystości.
Zatem zbiór możliwych wyników zawiera się w zbiorze
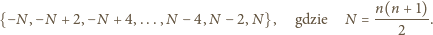
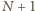 elementów. Wykażemy, że każdy
element jest możliwym wynikiem.
elementów. Wykażemy, że każdy
element jest możliwym wynikiem.
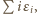 gdzie
gdzie
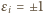 i nie wszystkie
i nie wszystkie
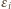 są równe
są równe
 Zamieniamy ciąg
Zamieniamy ciąg
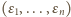 na ciąg
na ciąg
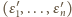 określony następująco:
określony następująco:
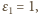 bierzemy
bierzemy
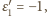 pozostałe
pozostałe
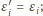
 znajdujemy najmniejszy
numer
znajdujemy najmniejszy
numer
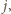 dla którego
dla którego
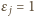 (więc
(więc
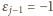 );
przyjmujemy
);
przyjmujemy
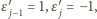 pozostałe
pozostałe
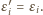
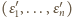 ma wynik
ma wynik
 Startując od prymusa z wektorem
Startując od prymusa z wektorem
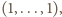 czyli
z wynikiem
czyli
z wynikiem
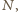 możemy w opisany sposób wygenerować
kolejno wyniki
możemy w opisany sposób wygenerować
kolejno wyniki
 itd., aż do
itd., aż do
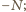 łącznie
łącznie
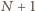 wyników.
wyników.
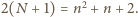
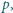 dla której
dla której
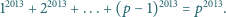
 zachodzi
zachodzi
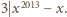 Stąd
Stąd

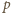 jest postaci
jest postaci
 to wówczas
to wówczas
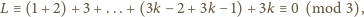
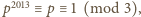 więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
więc równanie nie ma rozwiązania
w tym przypadku. Podobnie stwierdzamy, że dla
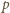 postaci
postaci
 równanie jest sprzeczne. Zatem jedyna możliwość to
równanie jest sprzeczne. Zatem jedyna możliwość to
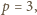 ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.
ale łatwo sprawdzić, że wtedy równanie również jest
sprzeczne.

 oraz
oraz
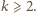 Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
Dziś
wiadomo, że jeśli równanie ma rozwiązanie dla jakiegoś
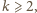 to
to
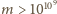 (zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
(zgrabny dowód i historia problemu są przedstawione
w artykule: P. Moore, A top hat for Moser’s four mathemagical rabbits, Amer.
Math. Monthly 118 (2011), 364-370).
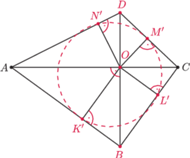
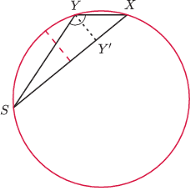
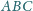 i takie punkty
i takie punkty
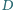 i
i
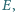 że
że
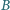 leży na odcinku
leży na odcinku
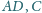 leży na odcinku
leży na odcinku
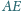 oraz
zachodzą równości
oraz
zachodzą równości
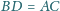 i
i
 (rysunek). Symetralna
odcinka
(rysunek). Symetralna
odcinka
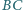 przecina
przecina
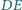 w punkcie
w punkcie
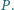 Udowodnić, że
kąty
Udowodnić, że
kąty
 i
i
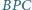 są równe.
są równe.

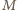 jest środkiem
jest środkiem
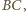 jego odległość od prostej
jego odległość od prostej
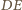 to średnia arytmetyczna odległości punktów
to średnia arytmetyczna odległości punktów
 i
i
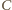 od
od
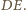 Jest ona równa średniej arytmetycznej odległości tych punktów
od
Jest ona równa średniej arytmetycznej odległości tych punktów
od
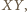 ponieważ
ponieważ
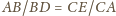 i
i
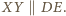 Zatem
Zatem
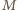 jest równo odległy od
jest równo odległy od
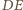 i
i
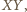 skąd
skąd
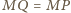 oraz
oraz
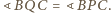
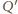 będzie takim punktem na półprostej
będzie takim punktem na półprostej
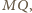 że
że
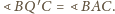 Z podobieństwa trójkątów równoramiennych
Z podobieństwa trójkątów równoramiennych
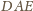 i
i
 mamy
mamy
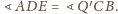 Zatem skoro na
czworokącie
Zatem skoro na
czworokącie
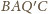 można opisać okrąg, to
można opisać okrąg, to
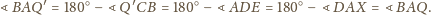
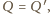 co daje tezę.
co daje tezę.
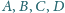 leżą, w tej właśnie kolejności, na prostej
leżą, w tej właśnie kolejności, na prostej
 przy
czym
przy
czym
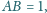
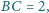
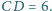 Rozstrzygnij, czy istnieje taki
punkt
Rozstrzygnij, czy istnieje taki
punkt
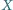 spoza prostej
spoza prostej
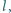 aby
aby


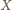 istnieje, to
istnieje, to
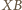 jest dwusieczną kąta
jest dwusieczną kąta
 zatem z twierdzenia o dwusiecznej
zatem z twierdzenia o dwusiecznej
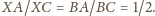 Punkty
Punkty
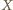 i
i
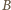 leżą więc na okręgu Apoloniusza dla punktów
leżą więc na okręgu Apoloniusza dla punktów
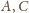 i stałej 1/2. Analogicznie punkty
i stałej 1/2. Analogicznie punkty
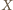 i
i
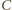 leżą na
okręgu Apoloniusza dla punktów
leżą na
okręgu Apoloniusza dla punktów
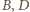 i stałej 1/3.
i stałej 1/3.

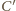 na prostej
na prostej
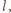 różny od
różny od
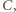 spełnia
warunek
spełnia
warunek
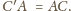 Wtedy
Wtedy
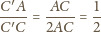
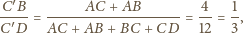
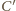 należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
należy do obydwu powyższych okręgów. Średnicą
pierwszego z nich jest więc
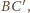 a drugiego –
a drugiego –
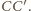 Stąd jedynym
ich wspólnym punktem jest
Stąd jedynym
ich wspólnym punktem jest
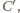 czyli
czyli
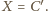 Ale wtedy
Ale wtedy
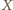 leży na prostej
leży na prostej
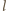 – sprzeczność.
– sprzeczność.
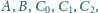 przy czym
przy czym
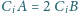 dla
dla
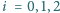 oraz
oraz
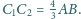 Udowodnij,
że kąt
Udowodnij,
że kąt
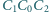 jest prosty i że punkty
jest prosty i że punkty
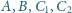 leżą na jednej
płaszczyźnie.
leżą na jednej
płaszczyźnie.

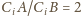 dla
dla
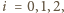 więc wszystkie punkty
więc wszystkie punkty
 leżą na sferze Apoloniusza dla punktów
leżą na sferze Apoloniusza dla punktów
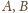 i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
i stałej 2
(zdefiniowanej analogicznie do okręgu). Jej średnicę wyznaczają punkty
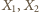 na prostej
na prostej
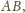 spełniające warunek
spełniające warunek
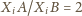 dla
dla
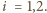 Wówczas
Wówczas
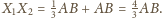
 także jest średnicą rozważanej sfery. Stąd
kąt
także jest średnicą rozważanej sfery. Stąd
kąt
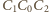 jest prosty, jako wpisany oparty na średnicy. Proste
jest prosty, jako wpisany oparty na średnicy. Proste
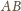 i
i
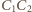 przecinają się (w środku sfery), więc punkty
przecinają się (w środku sfery), więc punkty
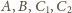 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
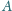 i
i
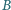 nie należą do płaszczyzny
nie należą do płaszczyzny
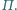 Wyznacz
zbiór wszystkich punktów
Wyznacz
zbiór wszystkich punktów
 o tej własności, że proste
o tej własności, że proste
 i
i
 tworzą z płaszczyzną
tworzą z płaszczyzną
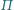 równe kąty.
równe kąty.
 oznaczają odpowiednio rzuty punktów
oznaczają odpowiednio rzuty punktów
 na
płaszczyznę
na
płaszczyznę
 Dla punktu
Dla punktu
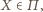 różnego od
różnego od
 i
i
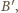 równość
równość
 zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
zachodzi wtedy i tylko
wtedy, gdy trójkąty prostokątne
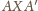 i
i
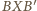 są podobne.
Równoważnie,
są podobne.
Równoważnie,
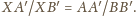 Jeśli
Jeśli
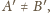 to
punkty
to
punkty
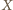 o żądanej własności tworzą okrąg Apoloniusza dla
punktów
o żądanej własności tworzą okrąg Apoloniusza dla
punktów
 i stałej
i stałej
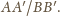 Jakie jest rozwiązanie, gdy
Jakie jest rozwiązanie, gdy
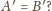 Czy możliwe, by
Czy możliwe, by
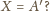
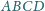 miara kąta wewnętrznego przy wierzchołku
miara kąta wewnętrznego przy wierzchołku
 jest większa od
jest większa od
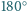 oraz zachodzi równość
oraz zachodzi równość
 Punkt
Punkt
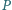 jest symetryczny do punktu
jest symetryczny do punktu
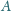 względem prostej
względem prostej
 Udowodnij, że
Udowodnij, że
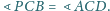
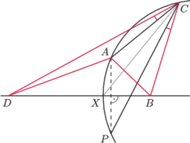
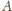 i
i
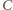 leżą na okręgu Apoloniusza dla punktów
leżą na okręgu Apoloniusza dla punktów
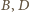 i stałej
i stałej
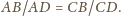 Z symetrii względem prostej
Z symetrii względem prostej
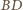 punkt
punkt
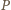 też na nim leży (
też na nim leży (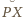 i
i
 są równe, więc
są równe, więc
 jest dwusieczną kąta
jest dwusieczną kąta
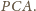 Jednocześnie
Jednocześnie
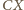 jest też dwusieczną kąta
jest też dwusieczną kąta
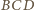 (własność z początku artykułu,
(własność z początku artykułu, 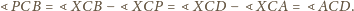
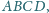 w którym
w którym
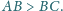 Na boku
Na boku
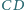 tego prostokąta skonstruuj takie punkty
tego prostokąta skonstruuj takie punkty
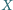 i
i
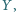 aby
aby
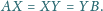
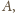 środka boku
środka boku
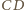 i stałej 2.
i stałej 2.
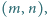 dla których
liczby
dla których
liczby

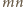 powinien być dzielnikiem liczb
powinien być dzielnikiem liczb
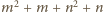 oraz
oraz
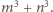 Zatem
Zatem
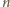 ma być dzielnikiem liczb
ma być dzielnikiem liczb
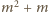 oraz
oraz
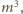 więc także liczby
więc także liczby
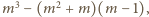 równej
równej
 Przez symetrię, liczba
Przez symetrię, liczba
 ma być dzielnikiem liczby
ma być dzielnikiem liczby
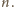 Dostajemy warunek
Dostajemy warunek
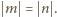
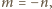 podane w zadaniu sumy wynoszą
podane w zadaniu sumy wynoszą
 oraz 0
(więc są całkowite). Jeśli zaś
oraz 0
(więc są całkowite). Jeśli zaś
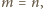 wynoszą one odpowiednio
wynoszą one odpowiednio
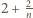 oraz
oraz
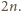 Są one obie całkowite wtedy i tylko wtedy, gdy
Są one obie całkowite wtedy i tylko wtedy, gdy
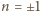 lub
lub
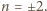
 gdzie
gdzie
 a ponadto cztery pary
a ponadto cztery pary
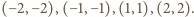
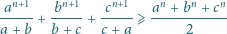
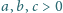 oraz liczb całkowitych
oraz liczb całkowitych
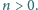
 liczb, mianowicie
liczb, mianowicie
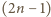 -krotnie powtórzonej liczby
-krotnie powtórzonej liczby
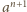 oraz liczb
oraz liczb
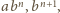 jest nie mniejsza od ich średniej geometrycznej, równej
jest nie mniejsza od ich średniej geometrycznej, równej
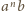 :
:
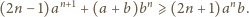
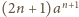 i po prostym przekształceniu
otrzymujemy
i po prostym przekształceniu
otrzymujemy

 oraz
oraz
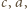 po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
po czym dodać te trzy nierówności, by uzyskać tezę
zadania.
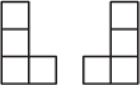
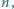 dla których kwadrat
złożony z
dla których kwadrat
złożony z
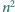 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytek pokazanych na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytek pokazanych na rysunku przez obrót o kąt
 lub
lub
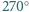 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

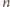 jest podzielne
przez
jest podzielne
przez
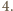
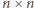 udało się pokryć dostępnymi płytkami.
Skoro pole płytki wynosi
udało się pokryć dostępnymi płytkami.
Skoro pole płytki wynosi
 to
to
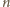 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
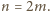 Rozważmy kolorowanie naszego kwadratu w pasy jak na rysunku.
Zauważmy, że każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy kolorowanie naszego kwadratu w pasy jak na rysunku.
Zauważmy, że każda płytka jest jednego z dwóch rodzajów: zawiera
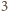 czarne pola lub
czarne pola lub
 czarne pole. Niech liczba płytek pierwszego
rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego
rodzaju wynosi
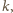 a drugiego
a drugiego
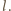 Zliczając czarne i białe pola,
otrzymujemy
Zliczając czarne i białe pola,
otrzymujemy
 oraz
oraz
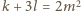 (dzięki temu,
że
(dzięki temu,
że
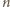 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
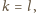 więc
więc
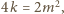 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
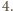
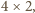 zatem
łatwo można znaleźć pokrycie kwadratu
zatem
łatwo można znaleźć pokrycie kwadratu
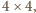 więc także
dowolnego kwadratu
więc także
dowolnego kwadratu
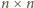 dla
dla
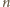 będącego wielokrotnością
będącego wielokrotnością
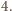
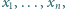 które są nie mniejsze niż
które są nie mniejsze niż
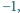 spełniają
równość
spełniają
równość
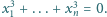 Udowodnić, że
Udowodnić, że
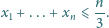
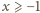 zachodzi
zachodzi
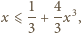

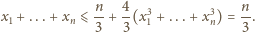

 o podstawach
o podstawach
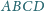 i
i
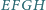 będących kwadratami, przy czym
będących kwadratami, przy czym
 i
i
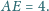 Punkt
Punkt
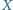 przesuwamy po przekątnej
przesuwamy po przekątnej
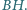 Znaleźć
minimalną wartość wyrażenia
Znaleźć
minimalną wartość wyrażenia
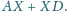
 wynosi
wynosi

 i
i
 na jednej
płaszczyźnie, dostajemy czworokąt
na jednej
płaszczyźnie, dostajemy czworokąt
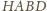 wpisany w okrąg.
wpisany w okrąg.
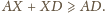 Równość zachodzi wtedy i tylko
wtedy, gdy
Równość zachodzi wtedy i tylko
wtedy, gdy
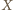 jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
jest punktem przecięcia przekątnych tego czworokąta.
Szukana minimalna wartość wyrażenia
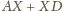 to długość
odcinka
to długość
odcinka
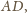 którą możemy obliczyć z twierdzenia Ptolemeusza:
którą możemy obliczyć z twierdzenia Ptolemeusza:
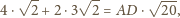
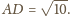
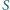 o środku w środku okręgu opisanego na trójkącie
o środku w środku okręgu opisanego na trójkącie
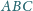 przecina krawędzie
przecina krawędzie
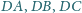 czworościanu
czworościanu
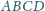 odpowiednio w punktach
odpowiednio w punktach
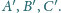 Płaszczyzny styczne
do tej sfery odpowiednio w punktach
Płaszczyzny styczne
do tej sfery odpowiednio w punktach
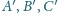 przecinają się w punkcie
przecinają się w punkcie
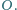 Wykazać, że punkt
Wykazać, że punkt
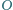 jest środkiem sfery opisanej na
czworościanie
jest środkiem sfery opisanej na
czworościanie

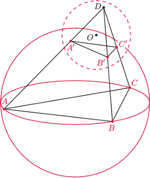
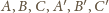 i sfera
opisana na czworościanie
i sfera
opisana na czworościanie
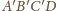 są prostopadłe. Zauważmy,
że
są prostopadłe. Zauważmy,
że
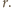 Rozważmy inwersję o środku
Rozważmy inwersję o środku
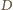 i promieniu
i promieniu
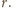 Zauważmy, że sfera
Zauważmy, że sfera
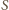 przechodzi na siebie, a punkty
przechodzi na siebie, a punkty
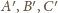 odpowiednio na
odpowiednio na
 (i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
(i na odwrót). Obrazem
drugiej z rozważanych sfer będzie więc płaszczyzna przechodząca przez
punkty
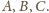 Jednakże środek sfery
Jednakże środek sfery
 leży właśnie na
płaszczyźnie
leży właśnie na
płaszczyźnie
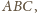 skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
skąd wniosek, że płaszczyzna ta jest do niej
prostopadła. A skoro inwersja zachowuje kąty między powierzchniami, to sfera
przechodząca przez punkty
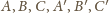 i sfera opisana na
czworościanie
i sfera opisana na
czworościanie
 też są prostopadłe.
też są prostopadłe.
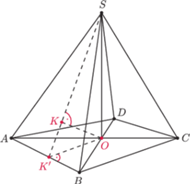
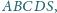 którego podstawą jest czworokąt wypukły
którego podstawą jest czworokąt wypukły
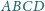 o prostopadłych przekątnych
o prostopadłych przekątnych
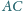 i
i
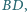 a rzutem
prostokątnym wierzchołka
a rzutem
prostokątnym wierzchołka
 na podstawę jest punkt
na podstawę jest punkt
 przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
przecięcia
przekątnych podstawy. Udowodnić, że rzuty prostokątne punktu
 na
ściany boczne ostrosłupa leżą na jednym okręgu.
na
ściany boczne ostrosłupa leżą na jednym okręgu.
 Weźmy rzut stereograficzny tej sfery z punktu
Weźmy rzut stereograficzny tej sfery z punktu
 na
płaszczyznę
na
płaszczyznę
 (
(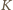 będzie rzutem prostokątnym
punktu
będzie rzutem prostokątnym
punktu
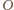 na ścianę
na ścianę
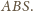 Płaszczyzna
Płaszczyzna
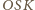 jest
prostopadła do krawędzi
jest
prostopadła do krawędzi
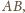 skąd wynika, że obraz
skąd wynika, że obraz
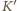 punktu
punktu
 w tym przekształceniu będzie rzutem prostokątnym punktu
w tym przekształceniu będzie rzutem prostokątnym punktu
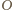 na krawędź
na krawędź
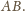 Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
Analogicznie udowodnimy, że obrazami
pozostałych rzutów są rzuty punktu
 na pozostałe boki czworokąta
na pozostałe boki czworokąta
 Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi –
Jednakże w czworokącie o prostopadłych przekątnych rzuty
prostokątne punktu przecięcia przekątnych leżą na jednym okręgu (łatwy
dowód tego faktu pozostawiamy Czytelnikowi – 
 czworościanu
czworościanu
 poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
poprowadzono
płaszczyznę styczną do sfery opisanej na tym czworościanie. Udowodnić, że
proste, wzdłuż których płaszczyzna ta przecina płaszczyzny ścian
 tworzą sześć równych kątów wtedy i tylko wtedy,
gdy
tworzą sześć równych kątów wtedy i tylko wtedy,
gdy

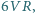 gdzie
gdzie
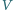 i
i
 oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
oznaczają odpowiednio objętość i promień sfery
opisanej na czworościanie (wzór Crellego).
 oraz
oraz
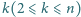 . Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
. Wyznaczyć
maksymalną liczbę wież, które można ustawić na szachownicy o rozmiarach
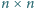 tak, by wśród dowolnie wybranych
tak, by wśród dowolnie wybranych
 wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).
wież były dwie,
które się wzajemnie atakują (przyjmujemy, że atakują się wzajemnie każde
dwie wieże, stojące w tym samym rzędzie poziomym lub pionowym,
niezależnie od tego, czy są pomiędzy nimi jeszcze jakieś inne wieże).
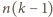 wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
wież w żądany sposób; wystarczy
zapełnić nimi prostokąt
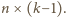 Pokażemy, że więcej się nie
da.
Pokażemy, że więcej się nie
da.
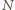 wież. Niech
wież. Niech
 będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
będzie
największą liczbą wież, jakie można wybrać spośród nich, by żadne dwie
się nie atakowały. Należy dowieść, że jeśli
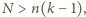 to
to
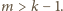 Wystarczy wykazać, że
Wystarczy wykazać, że
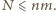
 wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
wież, z których żadne dwie nie stoją w jednym
wierszu ani jednej kolumnie. Permutując wiersze i kolumny, można przyjąć,
że te wieże stoją na polach
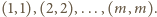 Podzielmy
szachownicę na cztery obszary
Podzielmy
szachownicę na cztery obszary
 gdzie
gdzie
 jest kwadratem
jest kwadratem
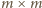 (na jego przekątnej stoją wybrane wieże),
(na jego przekątnej stoją wybrane wieże),
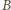 i
i
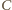 to
prostokąty
to
prostokąty
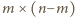 oraz
oraz
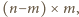 zaś
zaś
 to kwadrat
to kwadrat
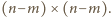 Wobec maksymalności
Wobec maksymalności
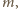 żadna wieża nie
znajduje się w obrębie kwadratu
żadna wieża nie
znajduje się w obrębie kwadratu
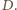
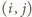 w prostokącie
w prostokącie
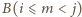 i symetryczne
do niego pole
i symetryczne
do niego pole
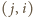 w prostokącie
w prostokącie
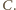 Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
Gdyby na obu tych polach
stały wieże, to usuwając z poprzednio ustalonego układu wieżę z pola
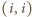 oraz dołączając wieże z pól
oraz dołączając wieże z pól
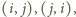 otrzymalibyśmy
układ
otrzymalibyśmy
układ
 wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
wież, stojących w różnych wierszach i kolumnach
– wbrew maksymalności
 Zatem co najwyżej połowa pól
w sumie prostokątów
Zatem co najwyżej połowa pól
w sumie prostokątów
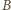 i
i
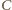 jest zajęta, czyli nie więcej
niż
jest zajęta, czyli nie więcej
niż
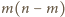 pól. Uwzględniając
pól. Uwzględniając
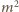 pól kwadratu
pól kwadratu
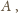 uzyskujemy oczekiwane oszacowanie:
uzyskujemy oczekiwane oszacowanie:

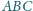 punkt
punkt
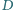 jest środkiem
przeciwprostokątnej
jest środkiem
przeciwprostokątnej
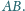 Dowieść, że prosta
Dowieść, że prosta
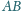 jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
jest styczna do
okręgu, którego średnica łączy środki okręgów opisanych na trójkątach
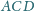 i
i
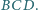

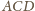 i
i
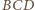 odpowiednio
przez
odpowiednio
przez
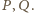 Niech
Niech
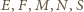 będą kolejno środkami
odcinków
będą kolejno środkami
odcinków
 Proste
Proste
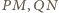 to symetralne
odcinków
to symetralne
odcinków
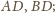 proste
proste
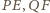 to symetralne odcinków
to symetralne odcinków
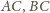 – przecinają się prostopadle w punkcie
– przecinają się prostopadle w punkcie
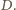 Okrąg
o średnicy
Okrąg
o średnicy
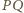 przechodzi więc przez punkt
przechodzi więc przez punkt
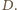 Ma on środek
w punkcie
Ma on środek
w punkcie
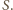
 jest środkiem odcinka
jest środkiem odcinka
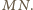 Zatem prosta
Zatem prosta
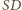 jest
równoległa do prostych
jest
równoległa do prostych
 i
i
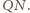 Prosta
Prosta
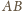 jest do nich
prostopadła. Wobec tego promień
jest do nich
prostopadła. Wobec tego promień
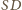 okręgu
okręgu
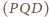 jest
prostopadły do
jest
prostopadły do
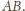 To znaczy, że ów okrąg jest styczny do prostej
To znaczy, że ów okrąg jest styczny do prostej
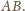

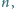 dla których kwadrat
złożony z
dla których kwadrat
złożony z
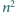 kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
kwadracików jednostkowych można pokryć
płytkami powstałymi z płytki pokazanej na rysunku przez obrót o kąt
 lub
lub
 w ten sposób, by płytki nie zachodziły na
siebie.
w ten sposób, by płytki nie zachodziły na
siebie.

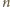 jest
podzielne przez
jest
podzielne przez
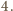
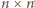 udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
udało się
pokryć dostępnymi płytkami. Skoro pole płytki wynosi
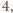 to
to
 musi być parzyste, powiedzmy
musi być parzyste, powiedzmy
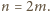 Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
Rozważmy
kolorowanie naszego kwadratu jak standardowej szachownicy i zauważmy, że
każda płytka jest jednego z dwóch rodzajów: zawiera
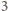 czarne pola
lub
czarne pola
lub
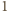 czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
czarne pole. Niech liczba płytek pierwszego rodzaju wynosi
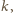 a drugiego
a drugiego
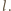 Zliczając czarne i białe pola, otrzymujemy
Zliczając czarne i białe pola, otrzymujemy
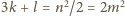 oraz
oraz
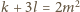 (dzięki temu, że
(dzięki temu, że
 jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
jest parzyste, mamy po równo pól czarnych i białych!). Stąd
w szczególności
 więc
więc
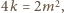 zatem
zatem
 jest
parzyste, a
jest
parzyste, a
 – podzielne przez
– podzielne przez
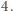
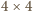 spełniające
warunki zadania, więc także dowolnego kwadratu
spełniające
warunki zadania, więc także dowolnego kwadratu
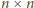 dla
dla
 będącego wielokrotnością
będącego wielokrotnością
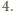
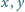 spełniają równość
spełniają równość
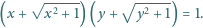
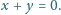
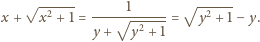
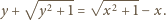
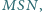 przy czym
przy czym
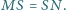 Punkt
Punkt
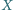 leży na krótszym łuku
leży na krótszym łuku
 okręgu o środku
okręgu o środku
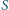 i promieniu
i promieniu
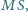 punkt
punkt
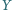 jest takim punktem odcinka
jest takim punktem odcinka
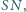 że proste
że proste
 i
i
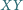 są równoległe. Znaleźć takie
położenie punktu
są równoległe. Znaleźć takie
położenie punktu
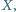 przy którym pole trójkąta
przy którym pole trójkąta
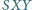 jest
największe.
jest
największe.
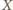 jest środkiem łuku
jest środkiem łuku
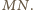
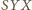 ma stałą miarę (niezależną od wyboru punktu
ma stałą miarę (niezależną od wyboru punktu
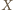 ),
a odcinek
),
a odcinek
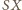 – stałą długość. Wszystkie rozważane trójkąty
– stałą długość. Wszystkie rozważane trójkąty
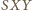 można więc wpisać w ten sam okrąg, przy czym kąt
można więc wpisać w ten sam okrąg, przy czym kąt
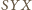 jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
jest oparty na ustalonej cięciwie. Pole takiego trójkąta wynosi
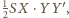 gdzie
gdzie
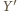 to rzut prostokątny punktu
to rzut prostokątny punktu
 na
na
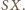 Jest ono największe, gdy
Jest ono największe, gdy
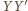 jest największe, czyli wtedy
i tylko wtedy, gdy
jest największe, czyli wtedy
i tylko wtedy, gdy
 Ale to jest równoważne temu, że
Ale to jest równoważne temu, że
 czyli temu, że
czyli temu, że
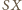 jest dwusieczną
kąta
jest dwusieczną
kąta

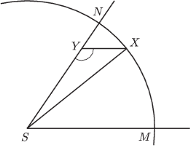
 kąt
kąt
 jest prosty. Wykaż, że
jest prosty. Wykaż, że

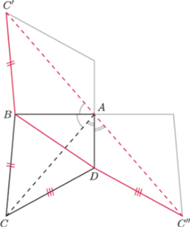
 symetrycznie względem prostych
symetrycznie względem prostych
 oraz
oraz
 i przyjmijmy oznaczenia jak na rysunku.
Wówczas
i przyjmijmy oznaczenia jak na rysunku.
Wówczas
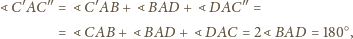
 i
i
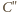 leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
leżą, w tej właśnie kolejności, na
jednej prostej. Ponadto
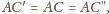 stąd
stąd
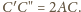
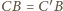 oraz
oraz
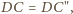 zatem
zatem
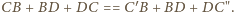 Teza wynika z faktu, że łamana
Teza wynika z faktu, że łamana
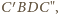 łącząca punkty
łącząca punkty
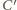 i
i
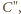 nie może być krótsza
niż odcinek
nie może być krótsza
niż odcinek
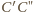 pomiędzy nimi:
pomiędzy nimi:
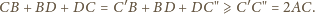
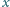 istnieją takie liczby niewymierne
istnieją takie liczby niewymierne
 i
i
 że
że

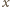 można wskazać odpowiednie liczby
można wskazać odpowiednie liczby
 i
i
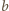 w następujący sposób.
w następujący sposób.
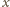 jest niewymierna, to niewymierne są także liczby
jest niewymierna, to niewymierne są także liczby
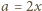 oraz
oraz
 (dlaczego?). Wówczas, oczywiście,
(dlaczego?). Wówczas, oczywiście,
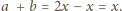
 jest wymierna, to liczba
jest wymierna, to liczba
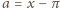 jest
niewymierna (dlaczego?). Wówczas, przyjmując
jest
niewymierna (dlaczego?). Wówczas, przyjmując
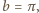 mamy
mamy
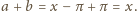
 zna osobę
zna osobę
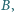 to także osoba
to także osoba
 zna osobę
zna osobę
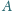 ).
).
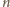 liczbę osób w rozważanej grupie. Wówczas każda
z nich może znać
liczbę osób w rozważanej grupie. Wówczas każda
z nich może znać
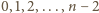 lub wszystkich
lub wszystkich
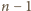 spośród
pozostałych; łącznie jest
spośród
pozostałych; łącznie jest
 możliwości – tyle, ile osób. Gdyby
każdy miał inną liczbę znajomych, to w rozważanym gronie byłaby
osoba
możliwości – tyle, ile osób. Gdyby
każdy miał inną liczbę znajomych, to w rozważanym gronie byłaby
osoba
 która nie zna nikogo, oraz osoba
która nie zna nikogo, oraz osoba
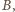 która zna
wszystkich. To prowadzi do sprzeczności, bo czy wtedy
która zna
wszystkich. To prowadzi do sprzeczności, bo czy wtedy
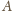 i
i
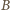 się
znają, czy nie? Wobec tego nie jest możliwe, by każdy miał inną liczbę
znajomych.
się
znają, czy nie? Wobec tego nie jest możliwe, by każdy miał inną liczbę
znajomych.

 kolegów podróż jest możliwa
i rozważmy
kolegów podróż jest możliwa
i rozważmy
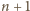 kolegów. Ponumerujmy ich zegarowo wokół okręgu:
kolegów. Ponumerujmy ich zegarowo wokół okręgu:
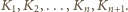
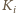 ma tyle paliwa, by
wystarczyło na podróż do
ma tyle paliwa, by
wystarczyło na podróż do
 (gdzie
(gdzie
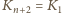 ). Gdyby bowiem
żaden kolega nie spełniał tego warunku, to łączna ilość posiadanego przez
wszystkich paliwa byłaby mniejsza, niż potrzeba do pełnego okrążenia,
sprzecznie z założeniem.
). Gdyby bowiem
żaden kolega nie spełniał tego warunku, to łączna ilość posiadanego przez
wszystkich paliwa byłaby mniejsza, niż potrzeba do pełnego okrążenia,
sprzecznie z założeniem.
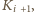 wraz ze swoim paliwem, złożyłby wizytę koledze
wraz ze swoim paliwem, złożyłby wizytę koledze
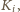 to z założenia indukcyjnego Fredek mógłby odwiedzić wszystkich
(
to z założenia indukcyjnego Fredek mógłby odwiedzić wszystkich
(
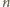 punktów na okręgu).
punktów na okręgu).
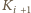 gościł
u
gościł
u
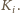 Wiemy, że gdyby u
Wiemy, że gdyby u
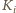 zatankował całe paliwo oferowane
przez
zatankował całe paliwo oferowane
przez
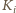 i
i
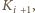 to mógłby dokończyć podróż. U kolegi
to mógłby dokończyć podróż. U kolegi
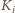 dostanie wystarczająco wiele, by dotrzeć do
dostanie wystarczająco wiele, by dotrzeć do
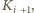 bo tak
wybraliśmy
bo tak
wybraliśmy
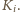 Potem u
Potem u
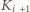 zatankuje resztę paliwa
oferowanego przez tych dwóch kolegów, więc – jak już wiemy – dokończy
podróż.
zatankuje resztę paliwa
oferowanego przez tych dwóch kolegów, więc – jak już wiemy – dokończy
podróż.
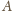 będzie miastem, z którego można dojechać do największej
liczby z pozostałych. Załóżmy, że istnieje miasto
będzie miastem, z którego można dojechać do największej
liczby z pozostałych. Załóżmy, że istnieje miasto
 do którego nie
można dotrzeć z
do którego nie
można dotrzeć z
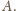 Droga łącząca
Droga łącząca
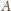 i
i
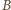 prowadzi więc
z
prowadzi więc
z
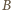 do
do
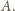 Wtedy z miasta
Wtedy z miasta
 można dojechać do
można dojechać do
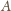 oraz dalej do wszystkich miast, do których można dotrzeć z
oraz dalej do wszystkich miast, do których można dotrzeć z
 Łącznie więc z
Łącznie więc z
 można dojechać do większej liczby miast
niż z
można dojechać do większej liczby miast
niż z
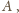 sprzecznie z wyborem
sprzecznie z wyborem