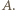Dla ustalonego, skończonego zbioru punktów na płaszczyźnie wyrażenie
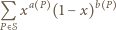
jest wielomianem zmiennej 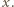 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 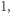 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 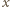 w przedziale
w przedziale 
Rozważmy losowe kolorowanie każdego z danych punktów na biało lub czarno. Załóżmy przy tym, że dowolny punkt malujemy na biało z prawdopodobieństwem 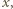 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 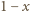 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 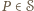 liczba
liczba 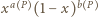 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 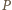 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 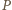 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 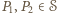 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
Suma
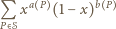
jest w tej sytuacji prawdopodobieństwem zdarzenia, w którym wierzchołki jednego z wielokątów 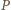 ze zbioru
ze zbioru 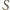 zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 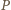 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
Szukanym wielokątem jest wielokąt 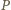 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 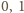 lub
lub 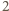 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
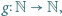 spełniającej warunek
spełniającej warunek 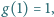 istnieje funkcja
istnieje funkcja 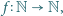 spełniająca warunki
spełniająca warunki 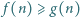 dla
dla 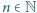 oraz
oraz 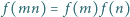 dla każdej pary liczb względnie pierwszych
dla każdej pary liczb względnie pierwszych 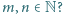 (
( 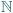 to zbiór wszystkich liczb całkowitych dodatnich).
to zbiór wszystkich liczb całkowitych dodatnich). łatwo wskazać funkcję
łatwo wskazać funkcję 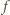 o wymaganych własnościach. Niech
o wymaganych własnościach. Niech 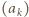 będzie rosnącym ciągiem wszystkich potęg liczb pierwszych:
będzie rosnącym ciągiem wszystkich potęg liczb pierwszych: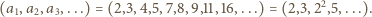
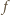 (o własności
(o własności 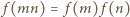 gdy
gdy 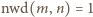 ) jest wyznaczona przez ciąg wartości
) jest wyznaczona przez ciąg wartości 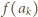 ; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech
; zaś podany warunek multyplikatywności nie stawia na owe wartości żadnych ograniczeń. Wobec tego konstruujemy taki ciąg indukcyjnie. Niech 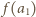 będzie dowolną liczbą naturalną większą od
będzie dowolną liczbą naturalną większą od 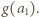
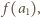 …,
…, 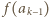 zostały już określone. Patrzymy na zbiór wszystkich liczb postaci
zostały już określone. Patrzymy na zbiór wszystkich liczb postaci 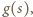 gdzie
gdzie  jest iloczynem różnych liczb ze zbioru
jest iloczynem różnych liczb ze zbioru 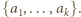 Określamy
Określamy 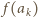 jako dowolną liczbę naturalną większą od wszystkich takich liczb
jako dowolną liczbę naturalną większą od wszystkich takich liczb 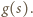
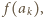 wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję
wraz z warunkiem multyplikatywności, jednoznacznie generuje funkcję 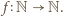 Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba
Spełnia ona także pozostały z zadanych warunków; jeśli bowiem liczba 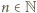 zostanie zapisana jako iloczyn
zostanie zapisana jako iloczyn 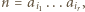 gdzie
gdzie 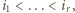 wówczas
wówczas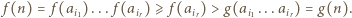
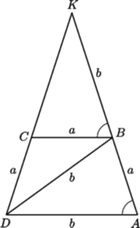
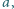 zaś pozostałe trzy mają jednakową długość
zaś pozostałe trzy mają jednakową długość 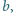 przy czym
przy czym 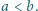 Wyznaczyć wszystkie możliwe wartości stosunku
Wyznaczyć wszystkie możliwe wartości stosunku 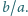
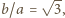 i jest to jedna z możliwych wartości rozpatrywanego stosunku. Dalej przyjmijmy, że nie pojawia się trójkąt równoboczny. Trzy odcinki długości
i jest to jedna z możliwych wartości rozpatrywanego stosunku. Dalej przyjmijmy, że nie pojawia się trójkąt równoboczny. Trzy odcinki długości 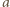 tworzą wówczas łamaną (nie zamkniętą), i tak samo trzy odcinki długości
tworzą wówczas łamaną (nie zamkniętą), i tak samo trzy odcinki długości 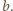 Można tak ustalić oznaczenia
Można tak ustalić oznaczenia 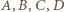 danych punktów, by
danych punktów, by
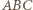 podstawa
podstawa 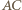 jest dłuższa niż ramiona. W trójkącie równoramiennym
jest dłuższa niż ramiona. W trójkącie równoramiennym 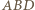 podstawa
podstawa 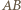 jest krótsza niż ramiona. Zatem
jest krótsza niż ramiona. Zatem 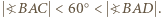
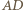 jest wspólnym bokiem przystających trójkątów równoramiennych
jest wspólnym bokiem przystających trójkątów równoramiennych 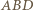 oraz
oraz 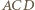 (o podstawach
(o podstawach 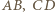 ). Te trójkąty muszą być położone symetrycznie - albo względem środka odcinka
). Te trójkąty muszą być położone symetrycznie - albo względem środka odcinka 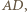 albo względem symetralnej tego odcinka. W pierwszym z tych przypadków powstałby równoległobok
albo względem symetralnej tego odcinka. W pierwszym z tych przypadków powstałby równoległobok 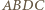 ; to jednak nie jest możliwe, skoro kąt
; to jednak nie jest możliwe, skoro kąt 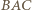 jest mniejszy od kąta
jest mniejszy od kąta 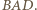
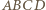 o podstawach
o podstawach 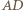 (dłuższej) i
(dłuższej) i 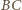 (krótszej). Półproste
(krótszej). Półproste 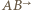 i
i 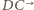 przecinają się w punkcie, który nazwiemy
przecinają się w punkcie, który nazwiemy 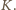 Trójkąty równoramienne
Trójkąty równoramienne 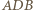 i
i 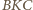 mają równe podstawy
mają równe podstawy 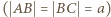 i równe kąty przy podstawie
i równe kąty przy podstawie 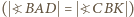 - są więc przystające. Stąd
- są więc przystające. Stąd 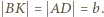 Trójkąt
Trójkąt 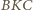 jest ponadto podobny do
jest ponadto podobny do 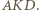 Otrzymujemy proporcję
Otrzymujemy proporcję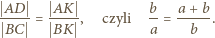
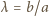 spełnia zatem równanie
spełnia zatem równanie 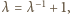 którego jedynym dodatnim pierwiastkiem jest
którego jedynym dodatnim pierwiastkiem jest 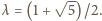 Realizację tej wartości uzyskujemy, biorąc jako
Realizację tej wartości uzyskujemy, biorąc jako 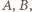
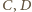 cztery wierzchołki pięciokąta foremnego.
cztery wierzchołki pięciokąta foremnego.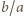 są liczby
są liczby 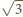 oraz
oraz 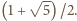
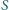 poza kartką, oraz punkt
poza kartką, oraz punkt 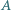 pomiędzy nimi. Korzystając wyłącznie z linijki, narysuj tę część prostej
pomiędzy nimi. Korzystając wyłącznie z linijki, narysuj tę część prostej 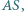 która mieści się na kartce.
która mieści się na kartce.
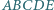 jest podstawą ostrosłupa
jest podstawą ostrosłupa 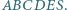 Płaszczyzna przecina krawędzie
Płaszczyzna przecina krawędzie 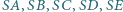 odpowiednio w punktach
odpowiednio w punktach 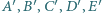 (różnych od wierzchołków ostrosłupa). Udowodnij, że punkty przecięcia przekątnych czworokątów
(różnych od wierzchołków ostrosłupa). Udowodnij, że punkty przecięcia przekątnych czworokątów 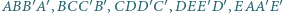 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.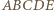 i
i 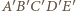 (rysunek podobny do
(rysunek podobny do 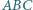 jest styczny do boków
jest styczny do boków 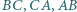 odpowiednio w punktach
odpowiednio w punktach 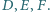 Udowodnij, że punkty
Udowodnij, że punkty 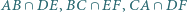 leżą na jednej prostej.
leżą na jednej prostej.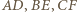 są współpękowe i wykorzystaj twierdzenie Desarguesa. Inne rozwiązanie opisano w deltoidzie 9/2014.
są współpękowe i wykorzystaj twierdzenie Desarguesa. Inne rozwiązanie opisano w deltoidzie 9/2014.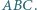 Punkty
Punkty 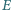 i
i 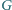 leżą na boku
leżą na boku 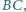 punkty
punkty 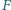 i
i 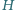 - na boku
- na boku 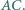 Punkty
Punkty 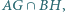
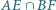 oraz punkt
oraz punkt 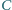 leżą na jednej prostej. Wykaż, że jeśli proste
leżą na jednej prostej. Wykaż, że jeśli proste 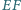 i
i 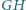 nie są równoległe, to przecinają się na prostej
nie są równoległe, to przecinają się na prostej 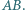
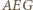 oraz
oraz 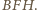
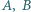 oraz plama oleju pomiędzy nimi. Poprowadź prostą przez punkty
oraz plama oleju pomiędzy nimi. Poprowadź prostą przez punkty 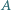 i
i 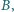 używając tylko linijki i nie brudząc jej w oleju.
używając tylko linijki i nie brudząc jej w oleju.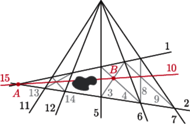
 i
i  różne od zera, że liczba
różne od zera, że liczba 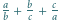 jest całkowita. Wykazać, że iloczyn
jest całkowita. Wykazać, że iloczyn 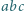 jest sześcianem liczby całkowitej.
jest sześcianem liczby całkowitej.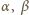 i
i 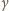 są niepodzielne przez liczbę pierwszą
są niepodzielne przez liczbę pierwszą 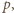 oraz że dla pewnej trójki liczb całkowitych nieujemnych
oraz że dla pewnej trójki liczb całkowitych nieujemnych 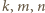 zachodzą równości
zachodzą równości 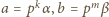 i
i 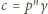 (w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn
(w dalszym ciągu myślę, że zadanie nie jest trudne). Aby wykazać, że iloczyn 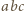 jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez
jest sześcianem pewnej liczby całkowitej, wystarczy przecież wykazać, iż każdy czynnik pierwszy występuje w rozkładzie tej liczby z wykładnikiem podzielnym przez 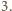 Mamy
Mamy 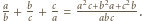 Mianownik tego ułamka jest podzielny przez liczbę
Mianownik tego ułamka jest podzielny przez liczbę 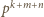 i niepodzielny przez
i niepodzielny przez 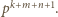 Zastąpienie uporządkowanej trójki liczb
Zastąpienie uporządkowanej trójki liczb 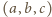 trójką
trójką 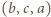 lub
lub 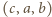 powoduje, że liczba
powoduje, że liczba 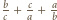 lub
lub 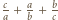 - więc ta z treści zadania - ma być całkowita (trójka
- więc ta z treści zadania - ma być całkowita (trójka 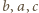 to jednak coś innego, bo na ogół
to jednak coś innego, bo na ogół 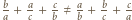 ). Można więc założyć, że
). Można więc założyć, że 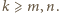 Mamy
Mamy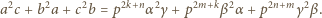
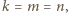 to
to 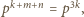 więc
więc 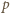 występuje w rozkładzie iloczynu
występuje w rozkładzie iloczynu 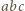 na czynniki pierwsze z wykładnikiem
na czynniki pierwsze z wykładnikiem 
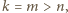 to
to 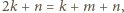
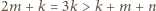 i
i 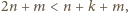 więc dwa z trzech składników licznika dzielą się przez
więc dwa z trzech składników licznika dzielą się przez 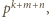 a trzeci nie, co oznacza, że liczba
a trzeci nie, co oznacza, że liczba 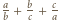 nie jest całkowita, wbrew założeniu.
nie jest całkowita, wbrew założeniu.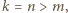 to
to 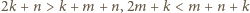 i
i 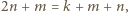 więc znów liczba
więc znów liczba 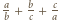 nie jest całkowita.
nie jest całkowita.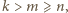 to
to 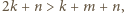
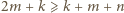 i
i 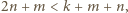 więc znów liczba
więc znów liczba 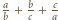 nie jest całkowita.
nie jest całkowita.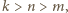 to
to 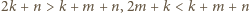 i
i 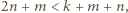 to teraz dwa składniki nie dzielą się przez
to teraz dwa składniki nie dzielą się przez 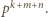 Ich suma może dzielić się przez
Ich suma może dzielić się przez 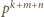 tylko wtedy, gdy
tylko wtedy, gdy 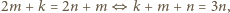 więc w tym wypadku liczba
więc w tym wypadku liczba 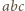 jest podzielna przez
jest podzielna przez 
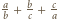 jest całkowita, to liczba pierwsza
jest całkowita, to liczba pierwsza 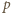 wchodzi w rozkład liczby
wchodzi w rozkład liczby 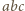 na czynniki pierwsze z wykładnikiem podzielnym przez
na czynniki pierwsze z wykładnikiem podzielnym przez 
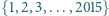 na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.
na jeden z czterech kolorów w taki sposób, że żaden rosnący 10-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze.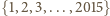 pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący
pokolorujemy na jeden z czterech kolorów w sposób losowy, to prawdopodobieństwo zdarzenia, w którym żaden rosnący 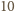 -wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem
-wyrazowy ciąg arytmetyczny o wyrazach z tego zbioru nie składa się z elementów o jednakowym kolorze, jest dodatnie. Zakładamy przy tym, że każdy element malujemy na dowolny z czterech kolorów z prawdopodobieństwem 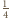 i że losowania są niezależne.
i że losowania są niezależne.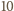 -wyrazowy ciąg arytmetyczny. Jest
-wyrazowy ciąg arytmetyczny. Jest 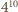 wszystkich możliwych pokolorowań tego ciągu, z których dokładnie
wszystkich możliwych pokolorowań tego ciągu, z których dokładnie 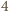 składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem
składają się wyłącznie z elementów o jednakowym kolorze. Prawdopodobieństwo tego, że ustalony ciąg składa się z elementów o jednakowym kolorze, wynosi zatem 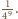 Oszacujmy od góry liczbę
Oszacujmy od góry liczbę 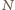 wszystkich rosnących
wszystkich rosnących 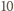 -wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy
-wyrazowych ciągów arytmetycznych o wyrazach w danym zbiorze. Każdy taki ciąg jest wyznaczony przez swój wyraz początkowy 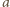 oraz różnicę
oraz różnicę 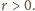 Spełnione są przy tym nierówności
Spełnione są przy tym nierówności 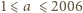 oraz
oraz 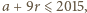 czyli
czyli 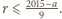 Dla ustalonego
Dla ustalonego  istnieje więc co najwyżej
istnieje więc co najwyżej 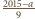 ciągów, których pierwszym wyrazem jest
ciągów, których pierwszym wyrazem jest 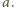 Otrzymujemy zatem nierówność
Otrzymujemy zatem nierówność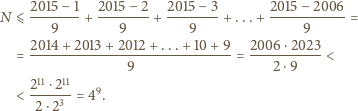
 z rozważanych ciągów w sposób dowolny i dla
z rozważanych ciągów w sposób dowolny i dla  oznaczmy przez
oznaczmy przez  zdarzenie, w którym
zdarzenie, w którym 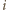 -ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas
-ty ciąg zawiera elementy wyłącznie jednego koloru. Z podstawowej własności prawdopodobieństwa (tzw. subaddytywności) otrzymujemy wówczas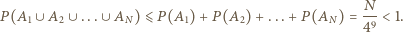
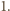 Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy.
Prawdopodobieństwo dopełnienia tego zdarzenia jest więc dodatnie, co oznacza, że w pewnym kolorowaniu żaden z rozważanych ciągów nie jest jednokolorowy. oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta
oznacza zbiór wszystkich wielokątów wypukłych o wierzchołkach w tym zbiorze (jako wielokąty wypukłe traktujemy również zbiór pusty, pojedyncze punkty oraz odcinki). Dla dowolnego wielokąta 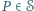 przez
przez 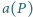 i
i 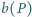 oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta
oznaczamy odpowiednio liczbę punktów z danego zbioru, które leżą na obwodzie i na zewnątrz wielokąta 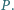 Wykazać, że dla każdej liczby rzeczywistej
Wykazać, że dla każdej liczby rzeczywistej  zachodzi równość
zachodzi równość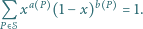
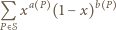
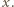 Aby wykazać, że jest to wielomian stale równy
Aby wykazać, że jest to wielomian stale równy 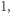 wystarczy sprawdzić, że żądana równość zachodzi dla liczb
wystarczy sprawdzić, że żądana równość zachodzi dla liczb 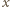 w przedziale
w przedziale 
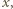 na czarno z prawdopodobieństwem
na czarno z prawdopodobieństwem 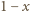 oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta
oraz że wszystkie losowania odbywają się niezależnie. Zauważmy, że wówczas dla ustalonego wielokąta 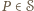 liczba
liczba 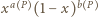 jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki
jest prawdopodobieństwem zdarzenia, w którym wszystkie wierzchołki 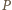 zostały pomalowane na biało, a punkty leżące na zewnątrz
zostały pomalowane na biało, a punkty leżące na zewnątrz 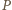 na czarno. Co więcej, dla dwóch różnych wielokątów
na czarno. Co więcej, dla dwóch różnych wielokątów 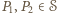 tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.
tego typu zdarzenia wykluczają się wzajemnie. Dla dowolnych dwóch różnych wielokątów wypukłych istnieje bowiem wierzchołek jednego z nich, który nie należy do drugiego. Gdyby opisane zdarzenia nie były rozłączne, to wierzchołek ten musiałby być pomalowany na dwa kolory, co jest, oczywiście, niemożliwe.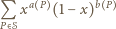
 ze zbioru
ze zbioru  zostały pomalowane na biało, zaś punkty leżące na zewnątrz
zostały pomalowane na biało, zaś punkty leżące na zewnątrz 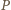 na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.
na czarno. Do rozwiązania zadania wystarczy więc stwierdzić, że jest to zdarzenie pewne - co oznacza, że w dowolnym pokolorowaniu taki wielokąt istnieje.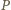 będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa
będący otoczką wypukłą białych punktów - czyli najmniejszym wielokątem wypukłym, który zawiera punkty białe (w przypadku gdy liczba punktów białych jest równa 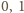 lub
lub 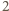 ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.
ich otoczką wypukłą jest odpowiednio zbiór pusty, punkt i odcinek). Jego wierzchołki są koloru białego, a każdy inny punkt biały znajduje się w jego wnętrzu.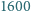 -osobowym stowarzyszeniu działa
-osobowym stowarzyszeniu działa 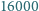 komisji, z których każda złożona jest z
komisji, z których każda złożona jest z 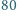 osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.
osób. Udowodnić, że pewne dwie różne komisje mają przynajmniej czterech wspólnych członków.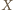 liczbę wspólnych członków tej pary. Niech
liczbę wspólnych członków tej pary. Niech 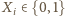 będzie funkcją charakterystyczną
będzie funkcją charakterystyczną 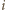 -tej osoby, czyli
-tej osoby, czyli 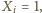 jeżeli
jeżeli 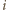 -ta osoba należy do obu wylosowanych komisji oraz
-ta osoba należy do obu wylosowanych komisji oraz 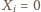 w przeciwnym przypadku. Funkcje
w przeciwnym przypadku. Funkcje 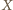 oraz
oraz 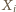 są zmiennymi losowymi. Ponieważ
są zmiennymi losowymi. Ponieważ 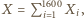 więc zachodzi równość
więc zachodzi równość ![|E[X]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/10x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba
Jednocześnie wprost z definicji wartości oczekiwanej wynika, że liczba ![| E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/11x-081b9846768cfbd773023286d0e3f4b920dfc8c7-im-66,57,43-FF,FF,FF.gif) jest w rzeczywistości prawdopodobieństwem tego, że
jest w rzeczywistości prawdopodobieństwem tego, że 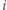 -ta osoba należy do obu z wylosowanych komisji. Jeśli przez
-ta osoba należy do obu z wylosowanych komisji. Jeśli przez 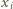 oznaczymy więc liczbę komisji, do których należy
oznaczymy więc liczbę komisji, do których należy 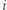 -ta osoba ze stowarzyszenia, to zachodzi równość
-ta osoba ze stowarzyszenia, to zachodzi równość![E[Xi]](/math/temat/matematyka/kombinatoryka/zadania/2015/03/29/zm-15_04-metody-3/15x-081b9846768cfbd773023286d0e3f4b920dfc8c7-dm-66,57,43-FF,FF,FF.gif)
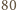 członków, to mamy ponadto
członków, to mamy ponadto 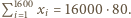 Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy
Wykorzystując nierówność między średnią arytmetyczną a kwadratową, otrzymujemy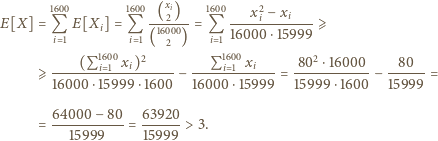
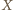 przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż
przyjmuje wyłącznie wartości całkowite, a więc skoro jej wartość oczekiwana jest większa niż 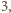 to co najmniej raz przyjmuje ona wartość nie mniejszą niż
to co najmniej raz przyjmuje ona wartość nie mniejszą niż 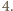 Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.
Istnieje więc para różnych komisji, która ma przynajmniej czterech wspólnych członków.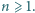 Niech
Niech 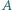 będzie ustalonym zbiorem
będzie ustalonym zbiorem 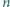 reszt z dzielenia przez
reszt z dzielenia przez 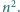 Udowodnić, że istnieje zbiór
Udowodnić, że istnieje zbiór 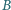 złożony z
złożony z 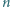 reszt z dzielenia przez
reszt z dzielenia przez 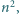 który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez
który spełnia następujący warunek: co najmniej połowa reszt z dzielenia przez 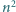 przystaje do liczby postaci
przystaje do liczby postaci 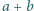 dla
dla 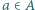 oraz
oraz 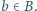
 niezależnych losowań ze zbioru reszt z dzielenia przez
niezależnych losowań ze zbioru reszt z dzielenia przez 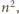 zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe
zakładając przy tym, że prawdopodobieństwo wylosowania dowolnej z reszt jest równe 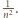 Z uzyskanych reszt tworzymy zbiór
Z uzyskanych reszt tworzymy zbiór 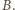 Ponieważ losowania są niezależne, może on składać się z mniej niż
Ponieważ losowania są niezależne, może on składać się z mniej niż 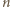 reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci
reszt, gdyż pewna reszta mogła zostać wylosowana więcej niż jeden raz. Jeżeli spełniony jest jednak warunek, w którym co najmniej połowa reszt może być zapisana w postaci 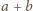 dla
dla 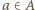 oraz
oraz 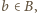 to możemy dopełnić zbiór
to możemy dopełnić zbiór 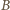 do zbioru
do zbioru 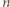 -elementowego w dowolny sposób i warunek ten pozostanie spełniony.
-elementowego w dowolny sposób i warunek ten pozostanie spełniony.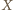 będzie liczbą reszt, które przystają do liczby postaci
będzie liczbą reszt, które przystają do liczby postaci 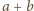 dla
dla 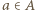 oraz
oraz 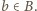 Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej
Wystarczy udowodnić, że wartość oczekiwana zmiennej losowej 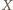 wynosi co najmniej
wynosi co najmniej 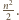 Ustalmy dowolną resztę
Ustalmy dowolną resztę 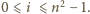 Ponieważ zbiór
Ponieważ zbiór 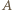 składa się z
składa się z  elementów, więc istnieje dokładnie
elementów, więc istnieje dokładnie  takich reszt
takich reszt 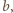 że
że 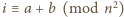 dla pewnego
dla pewnego 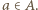 Prawdopodobieństwo tego, że ustalona reszta
Prawdopodobieństwo tego, że ustalona reszta 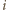 nie może być zapisana w żądanej postaci, wynosi zatem
nie może być zapisana w żądanej postaci, wynosi zatem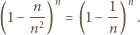
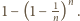 Korzystając z definicji wartości oczekiwanej oraz nierówności
Korzystając z definicji wartości oczekiwanej oraz nierówności 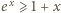 dla
dla 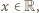 dostajemy
dostajemy![n2 ]=n2(1−(1−1))⩾n2(1−e−1)>n2(1−1)=n. E[X n22](/math/temat/matematyka/teoria_liczb/zadania/2015/03/29/zm-15_04-metody-4/19x-a985e63156cd220a3019db9f29340e69c1657a0c-dm-66,57,43-FF,FF,FF.gif)
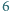 zadań. Każde z zadań zostało rozwiązane przez przynajmniej
zadań. Każde z zadań zostało rozwiązane przez przynajmniej 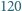 uczniów. Udowodnić, że istnieją tacy dwaj uczniowie, że każde z zadań zostało rozwiązane przez przynajmniej jednego z nich.
uczniów. Udowodnić, że istnieją tacy dwaj uczniowie, że każde z zadań zostało rozwiązane przez przynajmniej jednego z nich.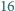 znajduje się
znajduje się 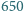 punktów. Mamy do dyspozycji pierścień, który powstał przez usunięcie koła o promieniu
punktów. Mamy do dyspozycji pierścień, który powstał przez usunięcie koła o promieniu 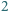 ze współśrodkowego z nim koła o promieniu
ze współśrodkowego z nim koła o promieniu 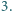 Wykazać, że ów pierścień można umieścić na płaszczyźnie w taki sposób, że przykrywa on przynajmniej
Wykazać, że ów pierścień można umieścić na płaszczyźnie w taki sposób, że przykrywa on przynajmniej 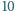 z danych punktów.
z danych punktów.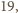 które jest współśrodkowe z danym. Udowodnij, że jeżeli środek pierścienia umieścimy w tym punkcie, to wartość oczekiwana liczby przykrytych punktów jest większa niż
które jest współśrodkowe z danym. Udowodnij, że jeżeli środek pierścienia umieścimy w tym punkcie, to wartość oczekiwana liczby przykrytych punktów jest większa niż 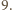


 znaleźć wartość sumy
znaleźć wartość sumy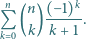
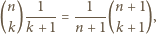
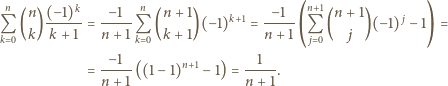
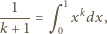
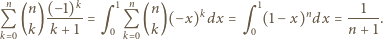

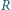 i
i  są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
są styczne zewnętrznie. Poprowadzono ich wspólną styczną i w obszar ograniczony przez nią i okręgi wpisano okrąg. Ile wynosi jego promień?
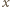 oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach
oznacza szukany promień. Jeden z trójkątów prostokątnych widocznych na rysunku ma przeciwprostokątną będącą sumą promieni o długościach 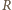 i
i  oraz przyprostokątną o długości
oraz przyprostokątną o długości 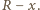 Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa
Z twierdzenia Pitagorasa otrzymujemy, że długość drugiej przyprostokątnej, a więc również długość odcinka pomiędzy odpowiednimi punktami styczności jest równa 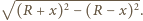
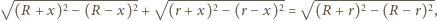
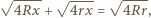
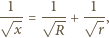
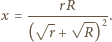

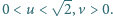
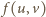 to kwadrat odległości między punktami
to kwadrat odległości między punktami 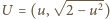 oraz
oraz 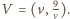
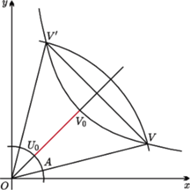
 zadanym równaniem
zadanym równaniem 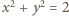 (a dokładniej na jego części znajdującej się w pierwszej ćwiartce układu współrzędnych), a drugi na gałęzi hiperboli
(a dokładniej na jego części znajdującej się w pierwszej ćwiartce układu współrzędnych), a drugi na gałęzi hiperboli 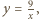 dla
dla 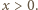 Aby znaleźć najmniejszą wartość funkcji
Aby znaleźć najmniejszą wartość funkcji 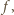 wystarczy znaleźć odległość okręgu
wystarczy znaleźć odległość okręgu 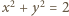 od hiperboli
od hiperboli 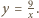 Niech
Niech 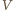 będzie wybranym punktem na hiperboli, a punkt
będzie wybranym punktem na hiperboli, a punkt 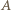 punktem przecięcia
punktem przecięcia  z odcinkiem
z odcinkiem 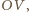 gdzie
gdzie 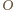 jest środkiem układu współrzędnych (patrz rysunek). Odległość punktu
jest środkiem układu współrzędnych (patrz rysunek). Odległość punktu 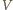 od
od  jest równa długości odcinka
jest równa długości odcinka 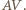 Niech punkt
Niech punkt 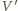 będzie symetryczny do
będzie symetryczny do 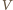 względem prostej
względem prostej 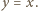 Odległość
Odległość 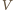 od
od  jest równa odległości
jest równa odległości 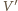 od
od 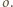 Ponadto, z wypukłości funkcji
Ponadto, z wypukłości funkcji 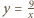 dla
dla 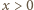 wynika, że punkt
wynika, że punkt 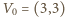 znajduje się po przeciwnej stronie prostej
znajduje się po przeciwnej stronie prostej 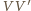 niż łuk okręgu o środku w punkcie
niż łuk okręgu o środku w punkcie  i promieniu równym długości odcinka
i promieniu równym długości odcinka 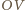 łączący punkty
łączący punkty 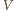 i
i 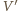 (patrz rysunek). Zatem odległość
(patrz rysunek). Zatem odległość 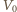 od
od  jest mniejsza niż odległość
jest mniejsza niż odległość 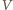 od
od 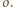 Z dowolności
Z dowolności 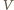 wynika, że najmniejsza wartość funkcji
wynika, że najmniejsza wartość funkcji 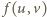 jest równa kwadratowi długości odcinka
jest równa kwadratowi długości odcinka 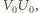 gdzie
gdzie 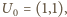 czyli
czyli 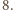
 znaleźć najmniejszą wartość sumy
znaleźć najmniejszą wartość sumy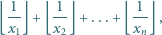
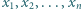 są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek
są dowolnymi liczbami rzeczywistymi dodatnimi, spełniającymi warunek 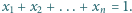
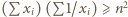 ; we wszystkich symbolach sumowania przyjmujemy
; we wszystkich symbolach sumowania przyjmujemy 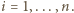 Przy warunku
Przy warunku 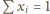 mamy więc
mamy więc 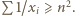 Dla każdej liczby rzeczywistej
Dla każdej liczby rzeczywistej 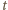 słuszne jest oszacowanie
słuszne jest oszacowanie 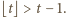 Stąd
Stąd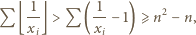
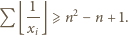
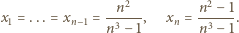
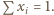 Dla
Dla 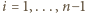 mamy przy tym
mamy przy tym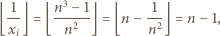
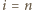 :
: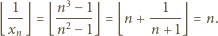
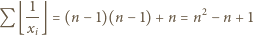
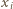 ; można dać wiele innych przykładów). Wniosek: liczba
; można dać wiele innych przykładów). Wniosek: liczba 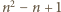 to szukane minimum.
to szukane minimum.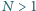 bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby
bezkwadratowa (tj. niepodzielna przez kwadrat żadnej liczby naturalnej większej od 1). Spośród wszystkich dodatnich dzielników liczby 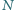 losujemy kolejno, bez zwracania, dwa dzielniki:
losujemy kolejno, bez zwracania, dwa dzielniki: 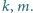 Rozważamy zdarzenia:
Rozważamy zdarzenia: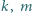 są względnie pierwsze;
są względnie pierwsze; jest podzielna przez
jest podzielna przez 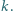
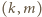 dzielników liczby
dzielników liczby 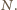 Zdarzenia
Zdarzenia 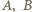 identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para
identyfikujemy z odpowiednimi podzbiorami zbioru wszystkich takich par. Gdy para 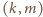 należy do
należy do 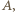 liczby
liczby 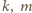 są względnie pierwszymi dzielnikami liczby
są względnie pierwszymi dzielnikami liczby 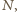 zatem także iloczyn
zatem także iloczyn 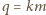 jest dzielnikiem
jest dzielnikiem 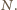 Oczywiście
Oczywiście 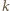 dzieli
dzieli 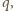 więc para
więc para 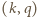 należy do
należy do 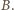
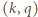 jest dowolną parą ze zbioru
jest dowolną parą ze zbioru 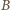 (więc
(więc 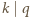 ), wtedy iloraz
), wtedy iloraz 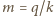 też jest dzielnikiem
też jest dzielnikiem 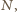 i to względnie pierwszym z
i to względnie pierwszym z 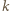 (bo gdyby
(bo gdyby 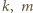 miały wspólny dzielnik
miały wspólny dzielnik 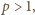 liczba
liczba 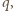 więc i
więc i 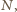 byłaby podzielna przez
byłaby podzielna przez 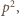 wbrew założeniu zadania). Zatem para
wbrew założeniu zadania). Zatem para 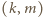 należy do
należy do 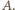
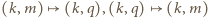 są wzajemnie odwrotne. Stąd wynika, że zbiory
są wzajemnie odwrotne. Stąd wynika, że zbiory 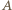 i
i 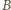 są równoliczne; zaś zdarzenia
są równoliczne; zaś zdarzenia 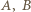 są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.
są (przy losowaniu ze zwracaniem) jednakowo prawdopodobne.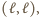 gdzie
gdzie 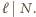 W poprzednim modelu, do zbioru
W poprzednim modelu, do zbioru 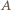 należała tylko jedna taka para
należała tylko jedna taka para 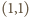 ; do
; do 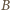 należały wszystkie. Więcej par zostało wyeliminowanych z
należały wszystkie. Więcej par zostało wyeliminowanych z 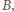 wobec czego (przy losowaniu bez zwracania) zdarzenie
wobec czego (przy losowaniu bez zwracania) zdarzenie 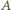 jest bardziej prawdopodobne niż
jest bardziej prawdopodobne niż 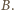
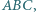 mając dany jego wierzchołek
mając dany jego wierzchołek 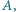 punkt
punkt 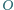 - środek okręgu opisanego i punkt
- środek okręgu opisanego i punkt 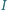 - środek okręgu wpisanego.
- środek okręgu wpisanego.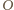 i promieniu
i promieniu 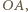
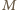 - jego punkt przecięcia z prostą
- jego punkt przecięcia z prostą 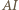 oraz okrąg o środku
oraz okrąg o środku 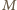 i promieniu
i promieniu 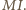 Na mocy twierdzenia
Na mocy twierdzenia 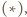 punkty przecięcia powyższych dwóch okręgów to wierzchołki
punkty przecięcia powyższych dwóch okręgów to wierzchołki 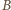 i
i 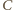 trójkąta.
trójkąta.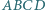 jest wpisany w okrąg
jest wpisany w okrąg 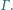 Punkt
Punkt 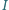 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 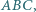 prosta
prosta 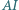 przecina okrąg
przecina okrąg 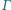 w punkcie
w punkcie 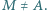 Punkt
Punkt 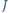 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 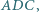 prosta
prosta 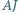 przecina okrąg
przecina okrąg 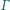 w punkcie
w punkcie 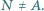 Wykaż, że jeżeli
Wykaż, że jeżeli 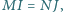 to
to 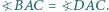
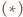 i założenia, zachodzi równość
i założenia, zachodzi równość 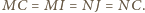 Stąd
Stąd 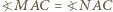 jako kąty wpisane w okrąg
jako kąty wpisane w okrąg 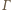 oparte na równych łukach. Wobec tego
oparte na równych łukach. Wobec tego 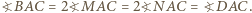
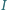 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 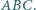 Wykaż, że okrąg opisany na trójkącie
Wykaż, że okrąg opisany na trójkącie 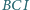 wyznacza na prostych
wyznacza na prostych 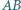 i
i 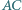 równe cięciwy.
równe cięciwy.
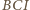 jest punkt
jest punkt 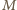 z twierdzenia
z twierdzenia  leży on na dwusiecznej kąta
leży on na dwusiecznej kąta 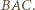 Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.
Z symetrii problemu okrąg ten wyznacza więc na ramionach kąta równe cięciwy.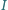 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 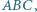 punkt
punkt 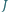 jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka
jest środkiem okręgu dopisanego do tego trójkąta. Wykaż, że środek odcinka  należy do okręgu opisanego na trójkącie
należy do okręgu opisanego na trójkącie 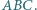
 leży w kącie
leży w kącie 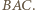 Dwusieczne kątów przyległych są prostopadłe, więc
Dwusieczne kątów przyległych są prostopadłe, więc 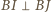 oraz
oraz 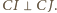 Wobec tego na czworokącie
Wobec tego na czworokącie 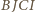 można opisać okrąg, którego środkiem jest środek
można opisać okrąg, którego środkiem jest środek 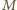 odcinka
odcinka 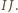 Okrąg ten jest opisany na trójkącie
Okrąg ten jest opisany na trójkącie 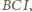 czyli
czyli 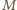 to punkt z twierdzenia
to punkt z twierdzenia 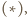 leży więc na okręgu opisanym na trójkącie
leży więc na okręgu opisanym na trójkącie 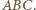
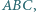 mając dane jego wierzchołki
mając dane jego wierzchołki 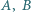 oraz promień okręgu wpisanego.
oraz promień okręgu wpisanego. jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 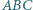 w punkcie
w punkcie 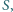 a do boków
a do boków 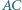 i
i 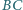 odpowiednio w punktach
odpowiednio w punktach 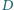 i
i 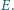 Wykaż, że jeśli
Wykaż, że jeśli 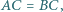 to środek okręgu wpisanego w trójkąt
to środek okręgu wpisanego w trójkąt 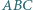 jest środkiem odcinka
jest środkiem odcinka 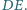
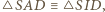 gdzie
gdzie 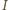 to środek odcinka
to środek odcinka 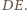
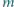 i
i  monetami. Ruch polega na usunięciu jednego ze stosów i podzieleniu drugiego na dwa niepuste. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy
monetami. Ruch polega na usunięciu jednego ze stosów i podzieleniu drugiego na dwa niepuste. Gracze wykonują ruchy na przemian. Jeśli któryś nie może wykonać ruchu, to przegrywa. Rozstrzygnąć, kto ma strategię wygrywającą, gdy 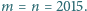
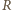 oznacza gracza rozpoczynającego, zaś
oznacza gracza rozpoczynającego, zaś 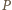 jego przeciwnika. Wykażemy, że
jego przeciwnika. Wykażemy, że 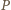 ma strategię wygrywającą, polegającą na pozostawianiu po każdym swoim ruchu dwóch stosów o nieparzystej liczbie monet.
ma strategię wygrywającą, polegającą na pozostawianiu po każdym swoim ruchu dwóch stosów o nieparzystej liczbie monet.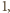 to
to 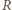 po wykonaniu swojego ruchu zostawi dla
po wykonaniu swojego ruchu zostawi dla 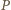 stos z parzystą liczbą monet (i drugi o nieparzystej liczbie monet). Wówczas
stos z parzystą liczbą monet (i drugi o nieparzystej liczbie monet). Wówczas 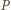 może usunąć stos o nieparzystej liczbie monet, a ten o parzystej liczbie monet podzielić na dwa stosy zgodnie ze swoją strategią.
może usunąć stos o nieparzystej liczbie monet, a ten o parzystej liczbie monet podzielić na dwa stosy zgodnie ze swoją strategią.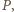 gdy zostawi on dla
gdy zostawi on dla 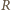 dwa jednomonetowe stosy.
dwa jednomonetowe stosy.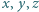 prawdziwa jest nierówność
prawdziwa jest nierówność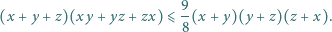
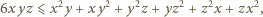
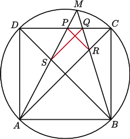
 leży na krótszym łuku
leży na krótszym łuku 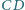 okręgu opisanego na kwadracie
okręgu opisanego na kwadracie 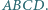 Prosta
Prosta 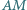 przecina
przecina 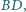
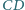 odpowiednio w punktach
odpowiednio w punktach 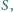
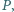 zaś prosta
zaś prosta 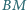 przecina
przecina 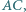
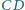 odpowiednio w punktach
odpowiednio w punktach 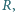
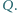 Udowodnić, że odcinki
Udowodnić, że odcinki 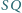 i
i 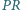 są prostopadłe.
są prostopadłe.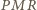 i
i 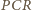 są równe (jako kąty wpisane oparte na ćwiartce okręgu), to na czworokącie
są równe (jako kąty wpisane oparte na ćwiartce okręgu), to na czworokącie 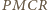 można opisać okrąg. Zatem
można opisać okrąg. Zatem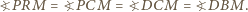
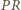 i
i 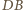 są równoległe. Rozważając czworokąt
są równoległe. Rozważając czworokąt 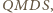 wykażemy analogicznie, że
wykażemy analogicznie, że 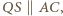 a stąd łatwo wywnioskować tezę.
a stąd łatwo wywnioskować tezę.
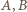 będą dwoma punktami z tej siódemki, których odległość jest maksymalna. Pozostałe punkty leżą w "soczewce", ograniczonej łukami okręgów o środkach
będą dwoma punktami z tej siódemki, których odległość jest maksymalna. Pozostałe punkty leżą w "soczewce", ograniczonej łukami okręgów o środkach 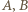 i promieniu
i promieniu 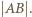 Skoro każdy z tych pięciu punktów ma wraz z
Skoro każdy z tych pięciu punktów ma wraz z 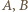 tworzyć trójkąt równoramienny, mogą one leżeć jedynie na owych łukach oraz odcinku
tworzyć trójkąt równoramienny, mogą one leżeć jedynie na owych łukach oraz odcinku 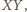 łączącym ich wspólne końce. Na samym odcinku
łączącym ich wspólne końce. Na samym odcinku 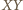 leżą co najwyżej dwa punkty (trójka współliniowa nie tworzy trójkąta). Pozostałe trzy punkty leżą na łukach
leżą co najwyżej dwa punkty (trójka współliniowa nie tworzy trójkąta). Pozostałe trzy punkty leżą na łukach 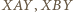 (bez końców
(bez końców 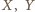 ).
).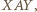 bowiem wraz z punktem
bowiem wraz z punktem 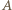 dałoby to czwórkę punktów, spośród których pewne trzy nie tworzyłyby trójkąta równoramiennego. Zatem na jednym łuku, np.
dałoby to czwórkę punktów, spośród których pewne trzy nie tworzyłyby trójkąta równoramiennego. Zatem na jednym łuku, np. 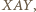 leży jeden punkt
leży jeden punkt 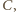 zaś na łuku
zaś na łuku 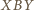 dwa punkty
dwa punkty 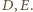 Przyjmijmy, że
Przyjmijmy, że 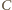 leży między
leży między 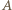 i
i 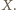
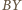 jest oddalony od
jest oddalony od 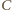 o odcinek dłuższy niż
o odcinek dłuższy niż 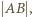 więc
więc 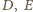 muszą być punktami łuku
muszą być punktami łuku 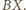 Każdy z odcinków
Każdy z odcinków 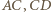 ma wtedy długość mniejszą niż
ma wtedy długość mniejszą niż 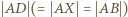 ; warunek równoramienności trójkąta
; warunek równoramienności trójkąta 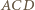 wymusza równość
wymusza równość 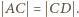 Zastępując w tym rozumowaniu
Zastępując w tym rozumowaniu 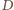 przez
przez 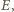 dostajemy równość
dostajemy równość 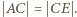 Wobec tego
Wobec tego 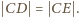 To już jest oczekiwana sprzeczność, bo jedynym punktem łuku
To już jest oczekiwana sprzeczność, bo jedynym punktem łuku 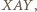 położonym w równych odległościach od
położonym w równych odległościach od 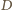 i
i 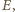 czyli na symetralnej odcinka
czyli na symetralnej odcinka 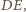 jest punkt
jest punkt