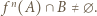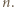O uogólnieniach i uszczególnieniach problemów matematycznych»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu O uogólnieniach i uszczególnieniach problemów matematycznych
- Publikacja w Delcie: wrzesień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (261 KB)
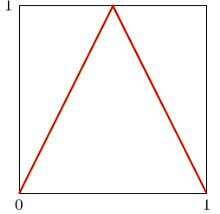
Wykres funkcji 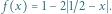
Niech ![| f [0,1] [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/1x-6ef1c75cd7890fac5a5a10e6c2a3afccfa359dba-im-2C,6B,73-FF,FF,FF.gif) będzie dane wzorem
będzie dane wzorem 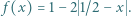 Niech ponadto
Niech ponadto 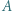 oraz
oraz 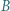 będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie
będą dowolnymi niepustymi przedziałami (otwartymi lub domkniętymi jedno- lub obustronnie), których końce są liczbami niewymiernymi. Uzasadnić, że istnieje takie 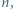 że
że 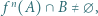 gdzie
gdzie 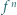 oznacza
oznacza  -krotne złożenie funkcji
-krotne złożenie funkcji 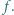
Uwaga: Zbiór pusty jest traktowany jako przedział, wobec tego założenie niepustego przedziału ma sens.

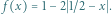
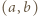 ma tę własność, że
ma tę własność, że ![fn((a,b)) = [0,1]](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/2x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) dla pewnego
dla pewnego 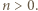 Niech
Niech 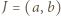 i
i 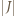 będzie długością tego przedziału. Zauważmy, że jeżeli
będzie długością tego przedziału. Zauważmy, że jeżeli 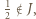 to
to 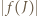 jest przedziałem dwukrotnie dłuższym niż
jest przedziałem dwukrotnie dłuższym niż 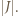 Tym samym kolejne przekształcenia
Tym samym kolejne przekształcenia 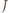 przez
przez 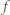 są przedziałami długości
są przedziałami długości 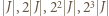 i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy
i tak dalej, o ile do żadnego z wymienionych zbiorów nie należy 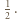 Wobec powyższego istnieje takie
Wobec powyższego istnieje takie 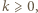 że
że 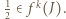 Ale
Ale 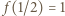 i
i 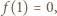 czyli
czyli 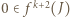 i wobec tego
i wobec tego 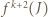 jest przedziałem postaci
jest przedziałem postaci 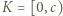 dla pewnego
dla pewnego 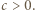 Teraz
Teraz 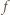 ponownie podwaja długość przedziału
ponownie podwaja długość przedziału 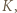 wobec tego dla pewnego
wobec tego dla pewnego 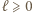 zachodzi
zachodzi 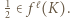 Tym samym
Tym samym ![[0, | 1/2]⊂ fℓ(K)](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/25x-3582530a21981c4662de24aae4547af0402ec105-im-66,57,43-FF,FF,FF.gif) i wystarczy jeszcze zauważyć, że
i wystarczy jeszcze zauważyć, że![[0,1] = f ([0,1/2]) ⊂ fℓ+1(K) = fℓ+1( fk+2(J)) = fk+ℓ+3(J).](/math/temat/matematyka/analiza/zadania/2020/08/26/zm-20-09-gr-2/26x-3582530a21981c4662de24aae4547af0402ec105-dm-66,57,43-FF,FF,FF.gif)
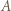 postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli
postulowany w treści zadania zawiera w sobie przedział otwarty oraz jeśli 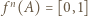 z przypadku ogólnego, to tym bardziej
z przypadku ogólnego, to tym bardziej