Uogólnijmy problem: udowodnimy, że jeżeli 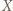 oraz
oraz 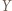 są zbiorami skończonymi o tej samej liczbie elementów oraz
są zbiorami skończonymi o tej samej liczbie elementów oraz 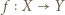 jest iniekcją, to
jest iniekcją, to 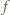 jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę
jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę 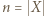 elementów zbioru
elementów zbioru 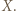 Oczywiście przypadek
Oczywiście przypadek 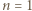 jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech
jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech 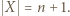 Niech
Niech 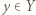 będzie takie, że
będzie takie, że 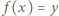 dla pewnego
dla pewnego 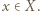 Takie
Takie 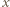 jest jedyne na mocy iniektywności, zatem można rozważyć funkcję
jest jedyne na mocy iniektywności, zatem można rozważyć funkcję 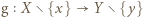 daną wzorem
daną wzorem 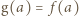 dla
dla 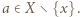 Wtedy
Wtedy 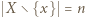 oraz
oraz 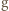 jest iniekcją. Istotnie, jeżeli
jest iniekcją. Istotnie, jeżeli 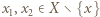 i
i 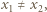 to
to 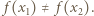 Zauważmy teraz, że
Zauważmy teraz, że 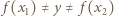 (ponownie korzystamy z iniektywności), zatem również
(ponownie korzystamy z iniektywności), zatem również 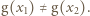 Tym samym
Tym samym 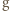 jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że
jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że 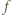 jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
Rozwiązanie problemu wyjściowego polega teraz na zastosowaniu udowodnionego przed chwilą ogólniejszego faktu dla 
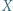 będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja
będzie zbiorem skończonym. Udowodnić, że dowolna iniekcja 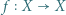 jest bijekcją.
jest bijekcją.
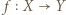 nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku
nazywamy iniekcją (funkcją różnowartościową), jeśli z warunku 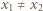 wynika, że
wynika, że 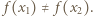 Funkcję
Funkcję 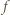 nazywamy surjekcją (funkcją na), gdy dla dowolnego
nazywamy surjekcją (funkcją na), gdy dla dowolnego 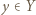 istnieje
istnieje 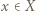 takie, że
takie, że 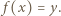 Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja.
Funkcja, która jest jednocześnie iniekcją i surjekcją, to bijekcja.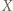 jest skończony, gdy istnieje liczba
jest skończony, gdy istnieje liczba 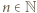 oraz bijekcja między zbiorami
oraz bijekcja między zbiorami 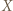 oraz
oraz 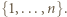 Piszemy wtedy również
Piszemy wtedy również 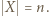
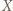 oraz
oraz 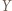 są zbiorami skończonymi o tej samej liczbie elementów oraz
są zbiorami skończonymi o tej samej liczbie elementów oraz 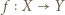 jest iniekcją, to
jest iniekcją, to 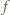 jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę
jest bijekcją. Rozwiązanie przebiega indukcyjnie ze względu na liczbę 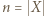 elementów zbioru
elementów zbioru 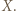 Oczywiście przypadek
Oczywiście przypadek 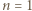 jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech
jest spełniony, przechodzimy zatem do kroku indukcyjnego. Niech 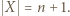 Niech
Niech 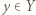 będzie takie, że
będzie takie, że 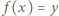 dla pewnego
dla pewnego 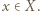 Takie
Takie 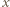 jest jedyne na mocy iniektywności, zatem można rozważyć funkcję
jest jedyne na mocy iniektywności, zatem można rozważyć funkcję 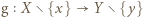 daną wzorem
daną wzorem 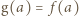 dla
dla 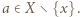 Wtedy
Wtedy 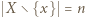 oraz
oraz 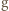 jest iniekcją. Istotnie, jeżeli
jest iniekcją. Istotnie, jeżeli 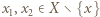 i
i 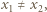 to
to 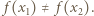 Zauważmy teraz, że
Zauważmy teraz, że 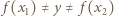 (ponownie korzystamy z iniektywności), zatem również
(ponownie korzystamy z iniektywności), zatem również 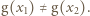 Tym samym
Tym samym 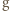 jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że
jest iniekcją, a więc z założenia indukcyjnego jest ona bijekcją. Stąd już łatwo wynika, że 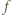 jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
jest bijekcją (dorzucamy po różnym od pozostałych punkcie do dziedziny i przeciwdziedziny).
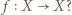 Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina
Usunięcie jednego elementu z dziedziny i przeciwdziedziny nie gwarantuje, że dziedzina i przeciwdziedzina 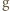 będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!
będą tym samym zbiorem, a tylko wtedy moglibyśmy skorzystać z założenia indukcyjnego!