Zadania z matematyki - VI 2020»Zadanie 1641
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - VI 2020
- Publikacja w Delcie: czerwiec 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Udowodnij, że liczba składająca się w zapisie dziesiętnym z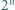 
jedynek ma co najmniej 
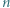różnych dzielników pierwszych.
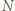będzie liczbą składającą się w zapisie dziesiętnym z 
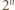jedynek. Mamy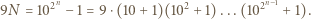
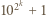i 
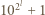są względnie pierwsze dla 
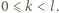Załóżmy, że obie te liczby są podzielne przez liczbę pierwszą 
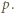Oczywiście liczba 
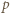jest nieparzysta. Ponieważ 
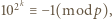więc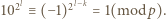 
Skoro jednak 
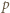dzieli 
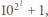to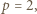 
co przeczy wcześniej poczynionej uwadze o nieparzystości 
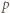i kończy rozwiązanie zadania.