Ekstrema»Zadanie 3
Na płaszczyźnie danych jest
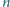 punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
Na płaszczyźnie danych jest
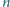 punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
punktów, przy czym odległości między
nimi są różne dla różnych par punktów. Każdy punkt łączymy odcinkiem
z jego najbliższym sąsiadem. Czy można otrzymać w ten sposób łamaną
zamkniętą?
Na płaszczyźnie danych jest
 punktów białych i
punktów białych i
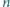 czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
czarnych,
żadne trzy nie są współliniowe. Wykaż, że można je tak połączyć
 odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
odcinkami, by każdy odcinek miał końce różnych kolorów i by
żadne dwa odcinki nie miały punktów wspólnych.
Na płaszczyźnie dany jest skończony zbiór punktów, z których każde trzy są wierzchołkami trójkąta o polu mniejszym lub równym 1. Wykaż, że istnieje trójkąt o polu nie większym niż 4, zawierający wszystkie te punkty.
W przestrzeni dany jest skończony zbiór punktów, z których każde cztery są wierzchołkami czworościanu o objętości mniejszej lub równej 1. Wykaż, że istnieje czworościan o objętości nie większej niż 27, zawierający wszystkie te punkty.
Na płaszczyźnie dany jest skończony zbiór punktów, z których żadne trzy nie leżą na jednej prostej. Wykaż, że można wśród nich znaleźć trzy takie, iż poprowadzony przez nie okrąg nie zawiera we wnętrzu innych punktów tego zbioru.
Każdy punkt płaszczyzny pomalowano na biało, czarno lub zielono. Udowodnić, że istnieją dwa punkty w odległości 1, które są tego samego koloru.
Znaleźć wszystkie trójkąty ostrokątne
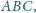 wpisane w ustalony
okrąg
wpisane w ustalony
okrąg
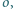 spełniające następujący warunek: środek ciężkości
spełniające następujący warunek: środek ciężkości
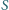 trójkąta
trójkąta
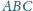 pokrywa się z ortocentrum
pokrywa się z ortocentrum
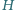 trójkąta
trójkąta
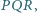 gdzie
gdzie
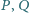 i
i
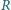 to odpowiednio punkty przecięcia
półprostych
to odpowiednio punkty przecięcia
półprostych
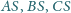 z okręgiem
z okręgiem
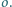
Niech
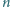 będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
będzie liczbą pięciocyfrową w zapisie dziesiętnym (pierwsza
cyfra jest różna od
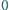 ) i niech
) i niech
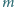 będzie liczbą czterocyfrową
powstałą z
będzie liczbą czterocyfrową
powstałą z
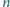 przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
przez wyrzucenie jej środkowej cyfry. Znaleźć wszystkie
takie liczby
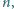 że liczba
że liczba
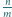 jest całkowita.
jest całkowita.
Dany jest przedział otwarty, którego końcami są kwadraty dwóch kolejnych
liczb naturalnych, większych od 1. Dowieść, że w tym przedziale
można znaleźć trzy różne liczby naturalne
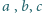 takie, że
takie, że
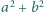 dzieli się przez
dzieli się przez

Zadanie 648 zaproponował pan Tomasz Ordowski.
Niech
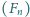 będzie ciągiem Fibonacciego:
będzie ciągiem Fibonacciego:

Udowodnić, że ciąg
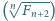 jest malejący.
jest malejący.
Multimilioner leci z Oslo (ok.
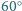 N,
N,
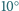 E) do cioci, mieszkającej
w Ameryce Południowej, w pewnym dużym mieście prawie na równiku.
Gdzie mieszka ciocia, jeśli prywatny odrzutowiec multimilionera, lecący do niej
najkrótszą drogą, startuje w tym celu dokładnie w kierunku zachodnim? Jaka
jest odległość pomiędzy Oslo a miastem cioci (obwód Ziemi to około
E) do cioci, mieszkającej
w Ameryce Południowej, w pewnym dużym mieście prawie na równiku.
Gdzie mieszka ciocia, jeśli prywatny odrzutowiec multimilionera, lecący do niej
najkrótszą drogą, startuje w tym celu dokładnie w kierunku zachodnim? Jaka
jest odległość pomiędzy Oslo a miastem cioci (obwód Ziemi to około
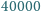 km)?
km)?
Ile trzeba zrobić zdjęć globusa, by w sumie uwiecznić na nich każde miejsce na Ziemi? Podpórkę od globusa, zasłaniającą być może fragmenty, zaniedbujemy.
Czy na powierzchni Ziemi istnieje taki trójkąt o bokach wyznaczonych przez najkrótsze drogi pomiędzy wierzchołkami, który ma wszystkie kąty proste?
Wędrowiec poszedł 10 km na południe, potem 10 km cały czas na wschód, wzdłuż równoleżnika, następnie 10 km na północ i wrócił w ten sposób do punktu wyjścia. Spotkał tam pewne zwierzę. Jeśli był to niedźwiedź, to jakiego koloru? Czy mógł to być pingwin?
Pola wszystkich przekrojów równoległościanu
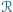 płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
płaszczyznami
przechodzącymi przez środki trzech jego krawędzi, z których żadne dwie nie
są równoległe i nie mają punktów wspólnych, są równe. Udowodnić, że
równoległościan
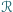 jest prostopadłościanem.
jest prostopadłościanem.
Czy w przestrzeni trójwymiarowej można znaleźć takie punkty
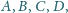 dla których spełnione są warunki:
dla których spełnione są warunki:

Dany jest czworościan
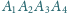 . Przez
. Przez
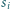 oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
oznaczmy długość
odcinka będącego częścią wspólną środkowej czworościanu poprowadzonej
z wierzchołka
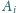 i kuli wpisanej w ten czworościan. Wiadomo, że
i kuli wpisanej w ten czworościan. Wiadomo, że
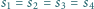 . Rozstrzygnąć, czy czworościan ten musi być
foremny.
. Rozstrzygnąć, czy czworościan ten musi być
foremny.
Sfera wpisana w czworościan jest styczna do dwóch ścian w środkach okręgów opisanych, a do trzeciej w ortocentrum. Dowieść, że czworościan ten jest foremny.
Czy mając dane promienie sfer dopisanych do czworościanu oraz promień sfery wpisanej w ten czworościan można wyznaczyć jego objętość?
Na szachownicy
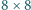 ułożono 21 klocków o wymiarach
ułożono 21 klocków o wymiarach
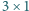 tak,
aby każdy klocek pokrywał całkowicie 3 pola. Które z pól mogło pozostać
wolne?
tak,
aby każdy klocek pokrywał całkowicie 3 pola. Które z pól mogło pozostać
wolne?
Na szachownicy
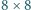 ułożono 12 klocków o wymiarach
ułożono 12 klocków o wymiarach
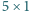 tak,
aby każdy klocek pokrywał całkowicie 5 pól. Które cztery pola pozostały
niepokryte?
tak,
aby każdy klocek pokrywał całkowicie 5 pól. Które cztery pola pozostały
niepokryte?
Zadanie 646 zaproponował pan Paweł Najman z Krakowa.
Niech
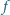 będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
będzie funkcją o wartościach rzeczywistych, określoną na
zbiorze liczb dodatnich, dwukrotnie różniczkowalną, spełniającą warunek
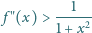 dla
dla
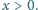 Czy taka funkcja może mieć asymptotę
przy
Czy taka funkcja może mieć asymptotę
przy
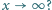
Czworokąt
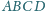 jest wpisany w okrąg. Boki
jest wpisany w okrąg. Boki
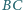 i
i
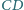 mają
jednakową długość. Na przedłużeniu odcinka
mają
jednakową długość. Na przedłużeniu odcinka
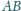 odkładamy odcinek
odkładamy odcinek
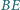 długości
długości
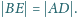 Dowieść, że
Dowieść, że
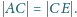
Udowodnić, że dla różnych liczb dodatnich
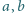 i liczby całkowitej
dodatniej
i liczby całkowitej
dodatniej
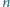 zachodzi nierówność
zachodzi nierówność
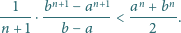
Każdy punkt płaszczyzny pomalowano na biało lub czarno. Rozstrzygnąć, czy istnieje niezdegenerowany do punktu odcinek jednokolorowy.
Dana jest rodzina
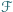 skończonych podzbiorów zbioru liczb całkowitych
dodatnich, taka że dowolne dwa różne zbiory tej rodziny mają wspólny element.
Czy istnieje taki skończony podzbiór
skończonych podzbiorów zbioru liczb całkowitych
dodatnich, taka że dowolne dwa różne zbiory tej rodziny mają wspólny element.
Czy istnieje taki skończony podzbiór
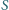 zbioru liczb całkowitych
dodatnich, że dla dowolnych
zbioru liczb całkowitych
dodatnich, że dla dowolnych
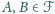 jest
jest