Zadanie ZM-1412
o zadaniu...
- Publikacja w Delcie: luty 2014
- Publikacja elektroniczna: 31-01-2014
Dane są liczby rzeczywiste
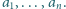 Niech
Niech
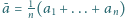 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
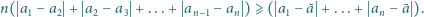 |
Dane są liczby rzeczywiste
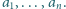 Niech
Niech
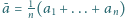 oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
oznacza
ich średnią arytmetyczną. Udowodnić, że prawdziwa jest nierówność
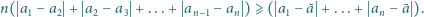 |
Zadania pochodzi z Obozu Naukowego po VIII Olimpiadzie Matematycznej Gimnazjalistów
Dany jest czworościan foremny o krawędzi 1 oraz punkt
 w jego
wnętrzu. Suma odległości punktu
w jego
wnętrzu. Suma odległości punktu
 od krawędzi tego czworościanu jest
równa
od krawędzi tego czworościanu jest
równa
 Wykaż, że
Wykaż, że
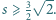
Czy istnieją czworościany
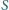 i
i
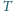 o następujących dwóch
własnościach:
o następujących dwóch
własnościach:
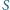 jest większa od objętości
czworościanu
jest większa od objętości
czworościanu
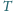 ;
;
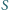 nie przekracza pola
żadnej ściany czworościanu
nie przekracza pola
żadnej ściany czworościanu
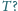
Rozstrzygnij, czy można obliczyć objętość czworościanu, znając pola jego czterech ścian oraz promień kuli opisanej.
Wyznacz promień kuli wpisanej w krawędzie czworościanu foremnego o objętości 1.
Wykaż, że jeśli w pewnym czworościanie dwie pary przeciwległych krawędzi są prostopadłe, to również trzecia para jest prostopadła.
Udowodnić, że dowolna liczba rzeczywista
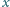 spełnia nierówność
spełnia nierówność
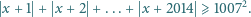 |
Rozpatrujemy takie ciągi
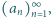 że
że
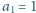 oraz, dla każdego
oraz, dla każdego
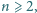
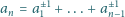
dla pewnego wyboru znaków
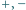 w wykładnikach. Znaleźć
najmniejszą możliwą wartość
w wykładnikach. Znaleźć
najmniejszą możliwą wartość
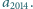
Zadanie 674 zaproponował pan Paweł Najman z Krakowa.
Znaleźć wszystkie funkcje
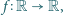 które spełniają układ równań
funkcyjnych
które spełniają układ równań
funkcyjnych
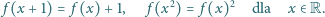
Czy istnieją cztery kolejne liczby całkowite dodatnie, których iloczyn,
powiększony o
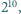 jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
jest kwadratem liczby całkowitej? Podać wszystkie
rozwiązania (jeśli istnieją).
Wykaż, że
Bilet do kina kosztuje 10 zł, w kasie jest dużo biletów i nie ma pieniędzy.
W kolejce stoi, w przypadkowej kolejności,
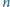 osób z banknotami 10
zł oraz
osób z banknotami 10
zł oraz
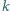 osób posiadających jedynie banknot 20 zł, przy czym
osób posiadających jedynie banknot 20 zł, przy czym
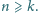 Jakie jest prawdopodobieństwo, że kasjerowi w trakcie obsługi
nie zabraknie reszty do wydawania?
Jakie jest prawdopodobieństwo, że kasjerowi w trakcie obsługi
nie zabraknie reszty do wydawania?
Zadanie ZM-1407 pochodzi z blogu T. Tao, http://terrytao.wordpress.com/.
Jaś, będąc na lotnisku, chce jak najszybciej przejść od punktu
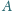 do
punktu
do
punktu
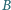 (w linii prostej). Idzie z prędkością
(w linii prostej). Idzie z prędkością
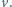 Na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
Na swojej
trasie ma odcinek, który pokonuje na ruchomej taśmie poruszającej się
z prędkością
 (czyli Jaś, idąc po taśmie, porusza się z prędkością
(czyli Jaś, idąc po taśmie, porusza się z prędkością
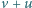 względem ziemi). Jaś ma jednak pewien zapas sił i może przez
czas
względem ziemi). Jaś ma jednak pewien zapas sił i może przez
czas
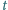 biec z prędkością
biec z prędkością
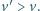 Czy powinien biec na taśmie,
czy poza nią? (Zakładamy dla uproszczenia, że taśma, jak i odcinek bez
taśmy są na tyle długie, że Jaś nie jest w stanie pokonać biegiem żadnego
z nich w całości.)
Czy powinien biec na taśmie,
czy poza nią? (Zakładamy dla uproszczenia, że taśma, jak i odcinek bez
taśmy są na tyle długie, że Jaś nie jest w stanie pokonać biegiem żadnego
z nich w całości.)
Zadanie 672 zaproponował pan Witold Bednarek z Łodzi.
Wykazać, że istnieje nieskończenie wiele par liczb wymiernych dodatnich
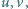 dla których liczba
dla których liczba

jest całkowita.
Płaszczyznę podzielono prostymi poziomymi i pionowymi na kwadraty jednostkowe i niektóre z tych kwadratów (skończenie wiele) zaczerniono. Każdy czarny kwadrat ma wspólne boki z dokładnie dwoma innymi czarnymi kwadratami. Ile może być czarnych kwadratów? Podać wszystkie możliwe wartości ich liczby.
Udowodnij, że w każdym czworościanie istnieje wierzchołek, przy którym trzy kąty płaskie są ostre.
Dany jest czworościan
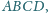 w którym
w którym
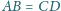 oraz
oraz
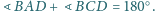 Udowodnij, że
Udowodnij, że
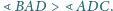
Czy istnieje taki ostrosłup czworokątny
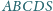 o podstawie
o podstawie
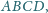 w którym
w którym
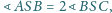
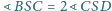 oraz
oraz
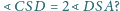

Na rysunku zmodyfikujmy kształty trójkątów tak, aby odpowiednie pary odcinków, które mają się skleić, nadal były równe oraz by przy każdym wierzchołku docelowego czworościanu dowolne dwa kąty płaskie były w sumie większe od trzeciego. Czy te warunki wystarczają, by otrzymać siatkę pewnego czworościanu?