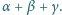Zadanie ZM-K44-590
o zadaniu...
- Publikacja w Delcie: marzec 2010
- Publikacja elektroniczna: 6 lipca 2010
Dowieść, że dla każdej parzystej liczby naturalnej
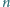 oraz dla każdej
liczby rzeczywistej
oraz dla każdej
liczby rzeczywistej
 zachodzi nierówność
zachodzi nierówność
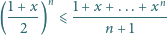
Dowieść, że dla każdej parzystej liczby naturalnej
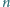 oraz dla każdej
liczby rzeczywistej
oraz dla każdej
liczby rzeczywistej
 zachodzi nierówność
zachodzi nierówność
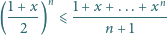
W każde pole tabelki o wymiarach
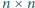 wpisujemy dodatnią
liczbę całkowitą niewiększą od
wpisujemy dodatnią
liczbę całkowitą niewiększą od
 tak, by w każdym wierszu oraz
w każdej kolumnie wszystkie liczby były równe lub wszystkie liczby
były różne. Niech
tak, by w każdym wierszu oraz
w każdej kolumnie wszystkie liczby były równe lub wszystkie liczby
były różne. Niech
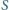 będzie sumą wszystkich liczb w tabelce.
Ile różnych wartości
będzie sumą wszystkich liczb w tabelce.
Ile różnych wartości
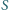 można w ten sposób uzyskać (dla
ustalonego
można w ten sposób uzyskać (dla
ustalonego
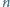 )?
)?
Niech
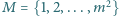 , gdzie
, gdzie
 jest ustaloną liczbą naturalną.
jest ustaloną liczbą naturalną.
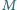 podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
podzbiorów niezawierających pary liczb,
których różnica dzieli się przez
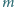 ?
?
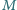 podzbiorów niezawierających pary liczb,
których różnica jest
równa
podzbiorów niezawierających pary liczb,
których różnica jest
równa
 ?
?Zadanie zaproponował pan Paweł Kubit z Krakowa.
Znaleźć wszystkie funkcje
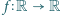 , spełniające równanie
, spełniające równanie
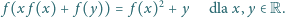
Punkty
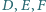 leżą odpowiednio na bokach
leżą odpowiednio na bokach
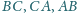 trójkąta
trójkąta
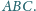 Okręgi wpisane w trójkąty
Okręgi wpisane w trójkąty
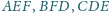 są
styczne do okręgu wpisanego w trójkąt
są
styczne do okręgu wpisanego w trójkąt
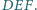 Udowodnij, że proste
Udowodnij, że proste
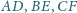 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Czworokąt
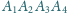 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
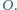 Punkty
Punkty
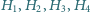 to ortocentra trójkątów, odpowiednio,
to ortocentra trójkątów, odpowiednio,
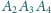 ,
,
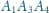 ,
,
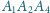 ,
,
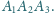 Wykaż, że czworokąty
Wykaż, że czworokąty
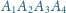 i
i
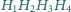 są przystające.
są przystające.
Dany jest czworościan
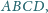 w którym
w którym
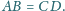 Sfera
wpisana w ten czworościan jest styczna do ścian
Sfera
wpisana w ten czworościan jest styczna do ścian
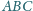 i
i
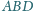 odpowiednio w punktach
odpowiednio w punktach
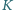 i
i
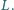 Dowieść, że jeżeli punkty
Dowieść, że jeżeli punkty
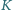 i
i
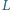 są środkami ciężkości ścian
są środkami ciężkości ścian
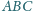 i
i
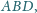 to czworościan
to czworościan
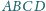 jest foremny.
jest foremny.
Czworościan
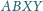 jest opisany na sferze. Punkty
jest opisany na sferze. Punkty
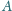 i
i
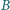 są
ustalone, a punkty
są
ustalone, a punkty
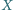 i
i
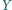 poruszają się. Udowodnić, że suma
kątów
poruszają się. Udowodnić, że suma
kątów

jest stała.
Sfera wpisana w czworościan
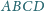 jest styczna do ściany
jest styczna do ściany
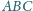 w punkcie
w punkcie
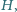 a sfera dopisana do tego czworościanu jest styczna do
ściany
a sfera dopisana do tego czworościanu jest styczna do
ściany
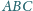 w punkcie
w punkcie
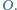 Dowieść, że jeżeli
Dowieść, że jeżeli
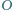 jest
środkiem okręgu opisanego na trójkącie
jest
środkiem okręgu opisanego na trójkącie
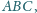 to
to
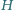 jest punktem
przecięcia wysokości tego trójkąta.
jest punktem
przecięcia wysokości tego trójkąta.
Sfera wpisana w czworościan
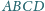 jest styczna do ścian
jest styczna do ścian
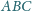 i
i
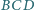 odpowiednio w punktach
odpowiednio w punktach
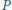 i
i
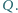 Dowieść, że
Dowieść, że
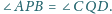
Dane są takie liczby wymierne
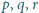 , dla których
, dla których
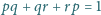 .
Wykazać, że liczba
.
Wykazać, że liczba
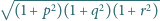
jest wymierna.
Czy istnieje taki wielościan wypukły, który ma nieparzystą liczbę krawędzi i którego każda ściana ma parzystą liczbę boków? Odpowiedź uzasadnij.
Dany jest okrąg o środku
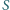 oraz punkt
oraz punkt
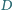 leżący na tym okręgu.
Cięciwa
leżący na tym okręgu.
Cięciwa
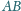 przecina odcinek
przecina odcinek
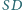 w punkcie
w punkcie
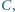 różnym od
punktu
różnym od
punktu
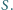 Wykaż, że
Wykaż, że
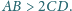
Dowieść, że dla każdej liczby naturalnej
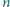 istnieje taki ciąg
arytmetyczny liczb naturalnych
istnieje taki ciąg
arytmetyczny liczb naturalnych
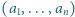 oraz taki ciąg geometryczny
liczb naturalnych
oraz taki ciąg geometryczny
liczb naturalnych
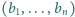 , że
, że

W pewnym czworościanie wszystkie sfery dopisane są styczne do ścian czworościanu w środkach okręgów wpisanych w te ściany. Udowodnić, że czworościan jest foremny.
Dowieść, że istnieje nieskończenie wiele par funkcji
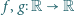 ,
mających pochodne wszystkich rzędów i spełniających warunki:
,
mających pochodne wszystkich rzędów i spełniających warunki:
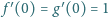 oraz
oraz
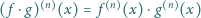
dla wszystkich
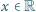 ,
,
Zadanie 582 zaproponował pan Witold Bednarek z Łodzi.
Dany jest
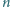 -elementowy zbiór
-elementowy zbiór
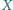
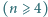 oraz
oraz
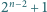 jego podzbiorów. Wykazać, że wśród tych podzbiorów
istnieją takie cztery, których część wspólna jest zbiorem pustym lub
jednoelementowym.
jego podzbiorów. Wykazać, że wśród tych podzbiorów
istnieją takie cztery, których część wspólna jest zbiorem pustym lub
jednoelementowym.
Wyznaczyć najmniejszą liczbą naturalną, której nie da się przedstawić w postaci

gdzie
 ,
,
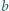 ,
,
 ,
,
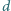 są liczbami całkowitymi dodatnimi.
są liczbami całkowitymi dodatnimi.
Na bokach dowolnego trójkąta zbudowano, na zewnątrz, trójkąty równoboczne. Udowodnij, że ich środki tworzą trójkąt równoboczny.
Niech
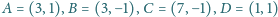 i
i
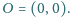 Oblicz
Oblicz
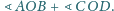
Trójkąty
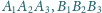 i
i
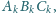 dla
dla
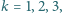 są równoboczne i zorientowane antyzegarowo. Wykaż, że trójkąt
są równoboczne i zorientowane antyzegarowo. Wykaż, że trójkąt
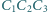 także spełnia te warunki.
także spełnia te warunki.
Trójkąty równoboczne
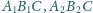 i
i
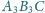 są zorientowane
antyzegarowo. Punkty
są zorientowane
antyzegarowo. Punkty
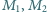 i
i
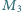 są środkami odpowiednio
odcinków
są środkami odpowiednio
odcinków
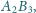
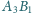 i
i
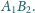 Udowodnij, że trójkąt
Udowodnij, że trójkąt
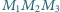 jest równoboczny i zorientowany zegarowo.
jest równoboczny i zorientowany zegarowo.
Oblicz sumę kątów