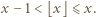Zera zmienią jednostkę w miliony»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Zera zmienią jednostkę w miliony
- Publikacja w Delcie: kwiecień 2020
- Publikacja elektroniczna: 1 kwietnia 2020
- Artykuł źródłowy w wersji do druku [application/pdf]: (395 KB)
Spośród liczb siedmiocyfrowych określonych w poprzednim zadaniu wybierzmy trzy, niekoniecznie różne. Czy ich suma może być kwadratem liczby naturalnej?
 nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby
nie występuje żadna z cyfr 1, 2, 9. Udowodnić, że w zapisie dziesiętnym liczby 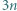 występuje co najmniej jedna z tych cyfr.
występuje co najmniej jedna z tych cyfr.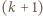 -cyfrowa. Możemy zapisać
-cyfrowa. Możemy zapisać 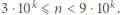 Wystarczy teraz wykazać, że jeśli liczba
Wystarczy teraz wykazać, że jeśli liczba 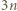 ma tyle samo cyfr co
ma tyle samo cyfr co 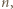 to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.
to jej pierwszą cyfrą jest 9, a jeśli ma o jedną cyfrę więcej, to jej pierwszą cyfrą jest 1 lub 2.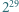 jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania
jest dziewięć cyfr, każda inna. Wiedząc to, bez obliczania 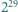 wyznaczyć cyfrę, która w tej liczbie nie występuje.
wyznaczyć cyfrę, która w tej liczbie nie występuje.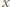 jest brakującą cyfrą, to suma cyfr liczby
jest brakującą cyfrą, to suma cyfr liczby 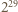 wynosi
wynosi 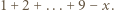 Zauważmy, że liczba
Zauważmy, że liczba 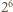 daje resztę 1 z dzielenia przez 9, więc liczba
daje resztę 1 z dzielenia przez 9, więc liczba 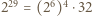 daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.
daje resztę 5 z dzielenia przez 9. Wystarczy porównać obie reszty.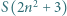 nie jest kwadratem liczby całkowitej dla żadnego naturalnego
nie jest kwadratem liczby całkowitej dla żadnego naturalnego 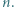
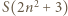 daje taką samą resztę z dzielenia przez 9, co
daje taką samą resztę z dzielenia przez 9, co 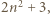 czyli 2, 3, 5 lub 8.
czyli 2, 3, 5 lub 8. i
i  zachodzi nierówność
zachodzi nierówność 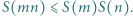
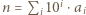 i
i 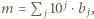 otrzymamy
otrzymamy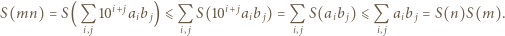
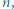 które spełniają równość
które spełniają równość 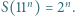
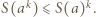 Wobec tego dla
Wobec tego dla 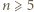 zachodzą nierówności
zachodzą nierówności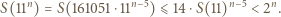
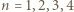 mamy
mamy 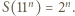
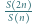 dla całkowitych dodatnich
dla całkowitych dodatnich 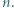

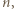 dla których osiągane są skrajne wartości.
dla których osiągane są skrajne wartości.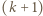 -cyfrową
-cyfrową 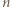 o pierwszej cyfrze
o pierwszej cyfrze 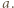 Iloczyn cyfr liczby
Iloczyn cyfr liczby 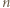 nie przekracza
nie przekracza 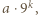 natomiast
natomiast 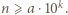 Taka liczba nie istnieje.
Taka liczba nie istnieje. liczby
liczby 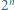 i
i 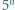 mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3.
mają taką samą pierwszą cyfrę. Wykazać, że tą cyfrą jest 3. będzie pierwszą cyfrą
będzie pierwszą cyfrą 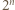 i
i 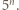 Zapiszmy
Zapiszmy 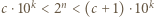 oraz
oraz 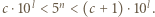 Mnożąc te dwie nierówności, otrzymamy
Mnożąc te dwie nierówności, otrzymamy 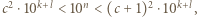 z czego wnioskujemy, że
z czego wnioskujemy, że 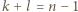 i w konsekwencji
i w konsekwencji 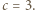
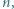 dla których
dla których 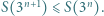
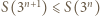 zachodzi tylko dla skończenie wielu
zachodzi tylko dla skończenie wielu 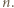 Wtedy istnieje takie
Wtedy istnieje takie 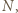 że dla wszystkich
że dla wszystkich 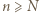 mamy
mamy 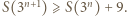 Stąd dla wszystkich
Stąd dla wszystkich 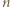 zachodzi nierówność
zachodzi nierówność 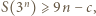 gdzie
gdzie  jest pewną stałą. Z drugiej strony,
jest pewną stałą. Z drugiej strony, 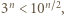 więc liczba
więc liczba 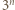 ma co najwyżej
ma co najwyżej 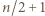 cyfr.
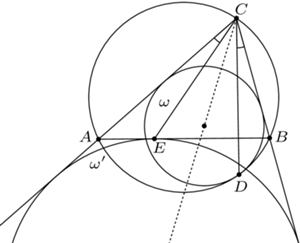
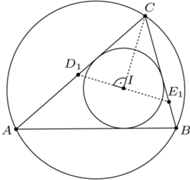
cyfr.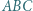 wpisany w okrąg
wpisany w okrąg  Okrąg
Okrąg 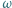 jest styczny do odcinków
jest styczny do odcinków 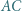 i
i 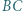 oraz do okręgu
oraz do okręgu  w punkcie
w punkcie 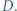 Okrąg
Okrąg 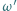 zaś jest dopisany do trójkąta
zaś jest dopisany do trójkąta 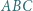 i styczny do boku
i styczny do boku 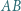 w punkcie
w punkcie 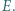 Wykazać, że
Wykazać, że 
 i promieniu
i promieniu 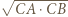 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 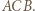 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 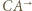 i
i 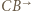 oraz prostą
oraz prostą 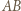 z okręgiem
z okręgiem 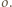 W takim razie okrąg
W takim razie okrąg 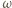 przejdzie na okrąg styczny do prostej
przejdzie na okrąg styczny do prostej 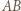 i półprostych
i półprostych 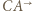 i
i 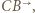 czyli na okrąg
czyli na okrąg 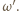 Stąd wniosek, że obrazem punktu
Stąd wniosek, że obrazem punktu 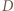 jest punkt
jest punkt 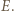 Półprosta
Półprosta 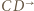 przejdzie więc na półprostą
przejdzie więc na półprostą 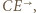 a skoro inwersja zachowuje kąty, to
a skoro inwersja zachowuje kąty, to 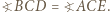
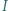 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 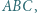 zaś
zaś  jest okręgiem opisanym na tym trójkącie. Okrąg
jest okręgiem opisanym na tym trójkącie. Okrąg 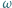 styczny do odcinków
styczny do odcinków 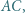
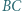 jest styczny do okręgu
jest styczny do okręgu  w punkcie
w punkcie 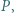 a
a 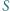 jest środkiem tego łuku
jest środkiem tego łuku 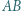 okręgu
okręgu  na którym leży punkt
na którym leży punkt  Wykazać, że punkty
Wykazać, że punkty  są współliniowe.
są współliniowe.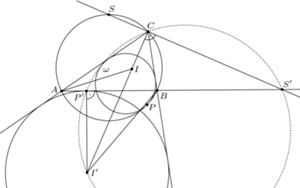
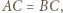 to punkty
to punkty 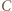 i
i 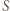 pokrywają się i punkty
pokrywają się i punkty  leżą na dwusiecznej
leżą na dwusiecznej 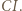 Dalej zakładamy, że
Dalej zakładamy, że 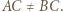 Wówczas punkty
Wówczas punkty 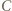 i
i 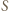 są różne, zaś proste
są różne, zaś proste 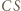 i
i 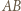 nie są równoległe. Rozważmy złożenie inwersji o środku
nie są równoległe. Rozważmy złożenie inwersji o środku 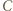 i promieniu
i promieniu 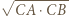 z symetrią względem dwusiecznej kąta
z symetrią względem dwusiecznej kąta 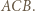 Przekształcenie to zamienia półproste
Przekształcenie to zamienia półproste 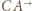 i
i 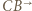 oraz prostą
oraz prostą 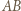 z okręgiem
z okręgiem 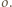 Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu
Tak jak w poprzednim zadaniu uzasadniamy, że obrazem okręgu 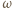 jest okrąg dopisany do trójkąta
jest okrąg dopisany do trójkąta 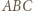 styczny do boku
styczny do boku 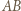 w punkcie
w punkcie 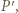 który jest obrazem punktu
który jest obrazem punktu 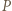 w tym przekształceniu. Ponieważ
w tym przekształceniu. Ponieważ 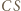 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 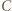 trójkąta
trójkąta 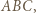 to proste
to proste 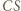 i
i 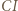 są prostopadłe. W takim razie obrazem punktu
są prostopadłe. W takim razie obrazem punktu 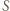 jest punkt
jest punkt 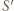 przecięcia prostej
przecięcia prostej 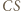 (która jest swoim własnym obrazem) z prostą
(która jest swoim własnym obrazem) z prostą 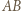 (która jest obrazem okręgu
(która jest obrazem okręgu  ). Niech
). Niech 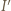 będzie obrazem punktu
będzie obrazem punktu 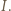 Wtedy z definicji inwersji mamy
Wtedy z definicji inwersji mamy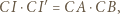
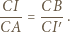
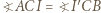 (bo inwersja zachowuje kąty) otrzymujemy, że trójkąty
(bo inwersja zachowuje kąty) otrzymujemy, że trójkąty 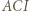 i
i 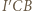 są podobne. W takim razie
są podobne. W takim razie 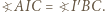 Ponieważ
Ponieważ 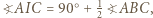 to mamy
to mamy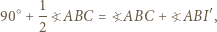
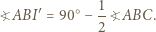
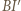 jest dwusieczną kąta zewnętrznego przy wierzchołku
jest dwusieczną kąta zewnętrznego przy wierzchołku 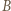 trójkąta
trójkąta 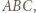 więc
więc 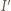 jest środkiem okręgu dopisanego do trójkąta
jest środkiem okręgu dopisanego do trójkąta 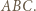 W takim razie
W takim razie 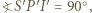 co wraz z równością
co wraz z równością 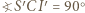 (bo
(bo 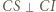 ) oznacza, że punkty
) oznacza, że punkty 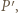
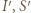 i
i 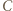 leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty
leżą na jednym okręgu. To zaś jest równoważne z tym, że punkty 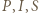 są współliniowe.
są współliniowe.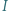 jest wpisany w trójkąt
jest wpisany w trójkąt 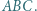 Okrąg
Okrąg 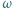 styczny do okręgu opisanego na trójkącie
styczny do okręgu opisanego na trójkącie 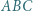 jest styczny do odcinków
jest styczny do odcinków 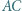 i
i 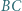 odpowiednio w punktach
odpowiednio w punktach 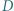 i
i 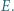 Wykazać, że punkt
Wykazać, że punkt 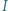 leży na odcinku
leży na odcinku 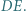
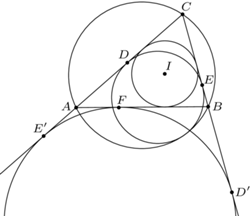
 to połowa obwodu trójkąta
to połowa obwodu trójkąta  to miara kąta
to miara kąta  zaś
zaś  to promień okręgu wpisanego w trójkąt
to promień okręgu wpisanego w trójkąt 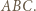 Inwersja o środku
Inwersja o środku 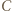 i promieniu
i promieniu 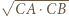 złożona z symetrią względem dwusiecznej kąta
złożona z symetrią względem dwusiecznej kąta 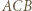 przeprowadza okrąg
przeprowadza okrąg 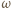 na okrąg dopisany do trójkąta
na okrąg dopisany do trójkąta 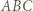 styczny do boku
styczny do boku 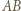 w punkcie
w punkcie 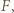 a punkty
a punkty 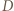 i
i 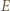 odpowiednio na punkty
odpowiednio na punkty 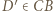 i
i 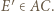 Ponieważ
Ponieważ 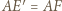 i
i 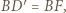 to
to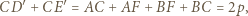
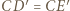 prowadzi do wniosku, że
prowadzi do wniosku, że 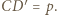 Z drugiej strony z definicji inwersji mamy
Z drugiej strony z definicji inwersji mamy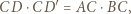
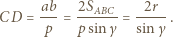
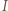 i prostopadła do prostej
i prostopadła do prostej 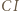 przecina boki
przecina boki 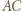 i
i 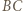 odpowiednio w punktach
odpowiednio w punktach 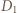 i
i 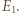 Skoro
Skoro 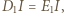 to odległość punktu
to odległość punktu 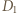 od prostej
od prostej 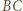 jest równa
jest równa 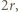 skąd wniosek, że
skąd wniosek, że 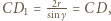 czyli
czyli 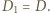 Analogicznie uzasadnimy, że
Analogicznie uzasadnimy, że 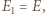 więc punkt
więc punkt 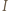 leży na odcinku
leży na odcinku 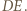
 jest wpisany w okrąg
jest wpisany w okrąg 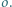 Punkty
Punkty 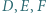 są środkami łuków
są środkami łuków 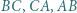 niezawierających pozostałych wierzchołków trójkąta. Punkty
niezawierających pozostałych wierzchołków trójkąta. Punkty 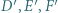 są symetryczne do punktów
są symetryczne do punktów 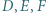 odpowiednio względem boków
odpowiednio względem boków 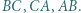 Wykazać, że punkty
Wykazać, że punkty 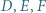 oraz ortocentrum trójkąta
oraz ortocentrum trójkąta 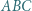 leżą na jednym okręgu.
leżą na jednym okręgu.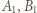 i
i 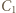 będą spodkami wysokości trójkąta
będą spodkami wysokości trójkąta 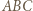 poprowadzonymi odpowiednio z wierzchołków
poprowadzonymi odpowiednio z wierzchołków 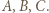 Ponieważ na czworokątach
Ponieważ na czworokątach 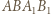 i
i 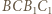 można opisać okręgi, to
można opisać okręgi, to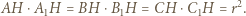
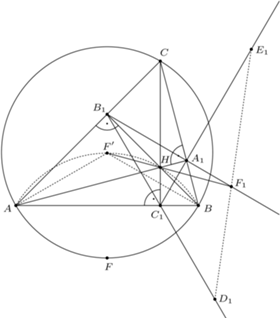
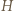 i promieniu
i promieniu  złożoną z symetrią środkową względem punktu
złożoną z symetrią środkową względem punktu 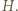 Obrazami punktów
Obrazami punktów 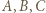 są zatem punkty
są zatem punkty 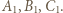 Ponieważ
Ponieważ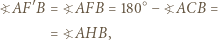
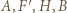 leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą
leżą na jednym okręgu, który w rozważanym przekształceniu przechodzi na prostą 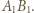 Obrazem punktu
Obrazem punktu 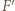 jest punkt
jest punkt 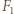 przecięcia prostych
przecięcia prostych 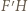 i
i 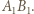 Analogicznie stwierdzamy, że w tym przekształceniu punkt
Analogicznie stwierdzamy, że w tym przekształceniu punkt 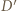 przechodzi na punkt
przechodzi na punkt 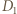 przecięcia prostych
przecięcia prostych 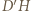 i
i 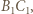 a punkt
a punkt 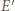 przechodzi na punkt
przechodzi na punkt 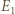 przecięcia prostych
przecięcia prostych 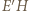 i
i 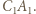
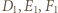 leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta
leżą na jednej prostej. Stosując twierdzenie Menelausa dla trójkąta 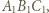 widzimy, że wystarczy wykazać, że
widzimy, że wystarczy wykazać, że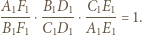
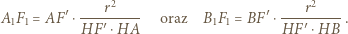
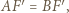 widzimy, że
widzimy, że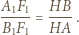

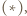 co kończy rozwiązanie.
co kończy rozwiązanie.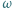 wpisany w trójkąt
wpisany w trójkąt 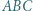 jest styczny do boku
jest styczny do boku 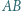 w punkcie
w punkcie 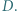 Okrąg
Okrąg 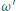 jest styczny do półprostych
jest styczny do półprostych 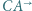 i
i 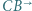 oraz jest styczny zewnętrznie w punkcie
oraz jest styczny zewnętrznie w punkcie 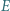 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 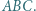 Wykazać, że
Wykazać, że 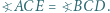
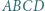 o podstawach
o podstawach 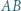 i
i 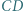 jest wpisany w okrąg
jest wpisany w okrąg 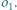 Okrąg
Okrąg 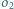 jest styczny do odcinków
jest styczny do odcinków 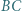 i
i 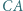 oraz jest styczny wewnętrznie do okręgu
oraz jest styczny wewnętrznie do okręgu 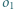 w punkcie
w punkcie 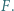 Okrąg wpisany w trójkąt
Okrąg wpisany w trójkąt 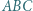 jest styczny do odcinka
jest styczny do odcinka 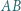 w punkcie
w punkcie 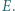 Dowieść, że punkty
Dowieść, że punkty 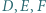 leżą na jednej prostej.
leżą na jednej prostej.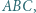 w którym
w którym 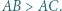 Punkty
Punkty 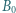 i
i 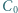 są odpowiednio środkami boków
są odpowiednio środkami boków 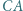 i
i 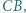 a punkt
a punkt 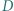 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 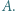 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 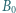 i
i 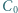 jest styczny do okręgu opisanego na trójkącie
jest styczny do okręgu opisanego na trójkącie 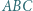 w punkcie
w punkcie 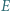 różnym od
różnym od 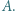 Udowodnić, że środek ciężkości trójkąta
Udowodnić, że środek ciężkości trójkąta 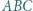 leży na prostej
leży na prostej 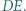
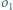 jest styczny do boków
jest styczny do boków 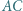 i
i 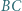 trójkąta
trójkąta 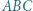 oraz do okręgu opisanego na tym trójkącie w punkcie
oraz do okręgu opisanego na tym trójkącie w punkcie 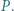 Okrąg
Okrąg 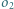 jest styczny do półprostych
jest styczny do półprostych 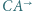 i
i 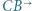 oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie
oraz jest styczny zewnętrznie do okręgu opisanego na trójkącie 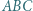 w punkcie
w punkcie 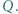 Wykazać, że
Wykazać, że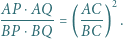
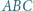 jest wpisany w okrąg
jest wpisany w okrąg 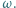 Prosta
Prosta 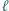 jest równoległa do prostej
jest równoległa do prostej 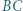 i przecina odcinki
i przecina odcinki 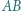 i
i 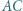 odpowiednio w punktach
odpowiednio w punktach 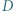 i
i 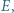 a okrąg
a okrąg 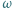 w punktach
w punktach 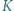 i
i 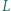 (gdzie
(gdzie 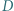 leży między punktami
leży między punktami 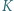 i
i 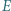 ). Okrąg
). Okrąg 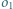 jest styczny do odcinków
jest styczny do odcinków 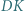 i
i 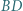 oraz do okręgu
oraz do okręgu  ; okrąg
; okrąg 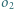 jest styczny do odcinków
jest styczny do odcinków 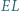 i
i 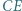 oraz do okręgu
oraz do okręgu  Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów
Wyznaczyć miejsce geometryczne punktów przecięcia wspólnych stycznych wewnętrznych okręgów 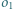 i
i 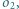 przy zmieniającym się położeniu prostej
przy zmieniającym się położeniu prostej 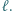
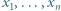 należą do odcinka
należą do odcinka ![[0,1].](/math/temat/matematyka/analiza/zadania/2020/02/29/zm-1632/2x-a703a273548e97ab80323cc80e76f4c2e0b71aa8-im-2C,6B,73-FF,FF,FF.gif) Udowodnić, że istnieje takie
Udowodnić, że istnieje takie 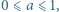 że
że 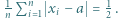
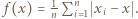 Ponieważ
Ponieważ 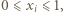 więc
więc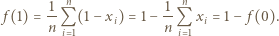
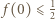 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy 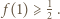 Teza wynika zatem z ciągłości funkcji
Teza wynika zatem z ciągłości funkcji 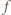 i własności Darboux funkcji ciągłych.
i własności Darboux funkcji ciągłych.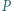 leży wewnątrz trójkąta ostrokątnego
leży wewnątrz trójkąta ostrokątnego 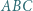 i nie jest środkiem okręgu
i nie jest środkiem okręgu 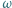 opisanego na tym trójkącie. Udowodnić, że wśród odcinków
opisanego na tym trójkącie. Udowodnić, że wśród odcinków 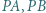 i
i 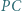 znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu
znajdują się odcinek krótszy oraz odcinek dłuższy od promienia okręgu 
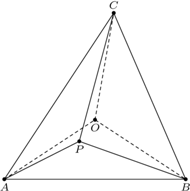
 leży wewnątrz trójkąta
leży wewnątrz trójkąta  i
i 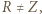 to
to 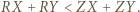 Aby go udowodnić, zauważmy najpierw, że
Aby go udowodnić, zauważmy najpierw, że 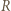 nie leży na co najmniej jednym z odcinków
nie leży na co najmniej jednym z odcinków 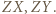 Bez straty ogólności przyjmijmy, że jest to
Bez straty ogólności przyjmijmy, że jest to 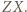 Niech
Niech 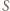 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 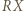 i
i 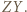 Wtedy z nierówności trójkąta:
Wtedy z nierówności trójkąta: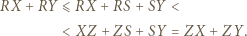
 będzie środkiem okręgu
będzie środkiem okręgu 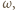 a
a  będzie promieniem tego okręgu. Punkt
będzie promieniem tego okręgu. Punkt 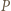 leży w co najmniej jednym z trójkątów
leży w co najmniej jednym z trójkątów 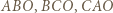 ; bez straty ogólności przyjmijmy, że jest to trójkąt
; bez straty ogólności przyjmijmy, że jest to trójkąt 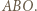 Podobnie,
Podobnie, 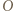 leży w którymś z trójkątów
leży w którymś z trójkątów 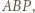
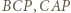 ; przyjmijmy, że jest to trójkąt
; przyjmijmy, że jest to trójkąt 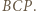 Zgodnie z lematem zachodzi
Zgodnie z lematem zachodzi 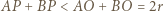 ; i analogicznie:
; i analogicznie: 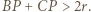 Zatem któryś z odcinków
Zatem któryś z odcinków 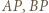 jest mniejszy od
jest mniejszy od  i któryś z odcinków
i któryś z odcinków 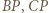 jest większy od
jest większy od 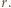
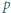 będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia
będzie liczbą pierwszą większą od 2. Udowodnić, że istnieje dokładnie jeden sposób przedstawienia 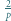 w postaci sumy
w postaci sumy 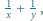 gdzie
gdzie 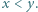
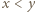 spełniają
spełniają 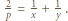 Równanie to można sprowadzić do postaci
Równanie to można sprowadzić do postaci 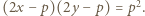 Ponieważ
Ponieważ 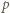 jest liczbą pierwszą, wynika stąd, że
jest liczbą pierwszą, wynika stąd, że 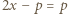 lub
lub 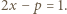 Pierwsza z tych możliwości oznaczałaby, że
Pierwsza z tych możliwości oznaczałaby, że 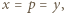 co przeczy zależności
co przeczy zależności 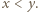 Musi być zatem
Musi być zatem 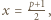 skąd
skąd 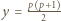 ; ponieważ
; ponieważ 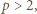 liczby te są całkowite i faktycznie spełniają wymaganą równość.
liczby te są całkowite i faktycznie spełniają wymaganą równość.
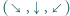 . Wiersze są numerowane od zera; zatem w
. Wiersze są numerowane od zera; zatem w  -tym wierszu jest
-tym wierszu jest 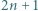 liczb dodatnich.
liczb dodatnich.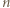 -tego wiersza jako kolejne współczynniki wielomianu stopnia
-tego wiersza jako kolejne współczynniki wielomianu stopnia 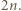 Mnożąc ów wielomian przez trójmian
Mnożąc ów wielomian przez trójmian 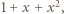 otrzymujemy wielomian stopnia
otrzymujemy wielomian stopnia 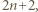 którego kolejnymi współczynnikami są wyrazy następnego wiersza tabeli - bo taka jest zasada generowania kolejnych wierszy. Stąd wniosek, że wyrazy
którego kolejnymi współczynnikami są wyrazy następnego wiersza tabeli - bo taka jest zasada generowania kolejnych wierszy. Stąd wniosek, że wyrazy  -tego wiersza to kolejne współczynniki wielomianu
-tego wiersza to kolejne współczynniki wielomianu 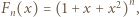 zapisanego w postaci rozwiniętej.
zapisanego w postaci rozwiniętej.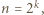 to wyrazy
to wyrazy 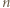 -tego wiersza, poza wspomnianymi trzema, są liczbami parzystymi. Uzasadnienie indukcyjne: tak jest dla
-tego wiersza, poza wspomnianymi trzema, są liczbami parzystymi. Uzasadnienie indukcyjne: tak jest dla 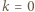 ; i jeśli tak jest dla
; i jeśli tak jest dla 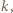 to podnosząc wielomian
to podnosząc wielomian 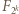 do kwadratu dostajemy wielomian
do kwadratu dostajemy wielomian 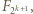 utworzony przez kwadraty składników wielomianu
utworzony przez kwadraty składników wielomianu 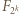 (ich współczynniki nie zmieniają parzystości) plus liczne podwojone iloczyny, dające współczynniki parzyste.
(ich współczynniki nie zmieniają parzystości) plus liczne podwojone iloczyny, dające współczynniki parzyste.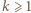 oraz
oraz 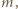 przy czym
przy czym 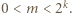 Wykażemy, że w wierszu o numerze
Wykażemy, że w wierszu o numerze 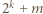 na pozycji
na pozycji 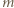 znajduje się liczba nieparzysta, zaś na pozycji
znajduje się liczba nieparzysta, zaś na pozycji 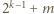 liczba parzysta.
liczba parzysta.
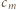 wyraża się wzorem
wyraża się wzorem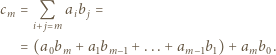
 w nawiasie są parzyste (jako współczynniki wielomianu
w nawiasie są parzyste (jako współczynniki wielomianu 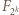 z pozycji nie skrajnych ani nie środkowej); liczba
z pozycji nie skrajnych ani nie środkowej); liczba 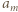 jest nieparzysta (środkowy wyraz
jest nieparzysta (środkowy wyraz 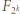 ). Zatem liczba
). Zatem liczba 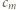 jest nieparzysta.
jest nieparzysta.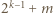 widzimy w wielomianie
widzimy w wielomianie 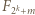 współczynnik
współczynnik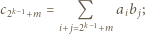
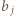 mamy tylko dla
mamy tylko dla 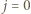 oraz
oraz 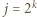 (środkowy wyraz w
(środkowy wyraz w 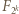 ); towarzyszą im czynniki
); towarzyszą im czynniki 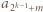 oraz
oraz 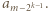 Te dwie liczby są położone w wierszu
Te dwie liczby są położone w wierszu 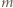 symetrycznie względem wyrazu środkowego
symetrycznie względem wyrazu środkowego 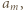 więc są równe.
więc są równe.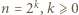 (bowiem gdy
(bowiem gdy 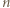 nie jest potęgą dwójki,
nie jest potęgą dwójki, 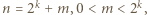 znaleziona liczba nieparzysta
znaleziona liczba nieparzysta 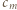 leży w wierszu
leży w wierszu 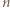 na pozycji
na pozycji 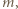 więc nie na skraju ani nie na środku).
więc nie na skraju ani nie na środku).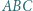 wysokość poprowadzona z wierzchołka
wysokość poprowadzona z wierzchołka 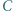 ma długość
ma długość 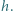 Punkty
Punkty 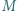 i
i 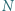 to (odpowiednio) środki boków
to (odpowiednio) środki boków 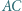 i
i 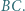 Okrąg przechodzący przez punkty
Okrąg przechodzący przez punkty 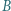 i
i 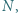 styczny do prostej
styczny do prostej 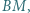 przecina prostą
przecina prostą 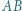 ponownie w punkcie
ponownie w punkcie 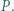 Wyznaczyć największą liczbę
Wyznaczyć największą liczbę 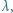 dla której (przy każdej takiej konfiguracji) odcinek
dla której (przy każdej takiej konfiguracji) odcinek 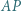 ma długość nie mniejszą niż
ma długość nie mniejszą niż 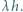

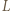 będzie środkiem boku
będzie środkiem boku 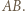 W okręgu
W okręgu 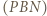 kąt wpisany oparty na cięciwie
kąt wpisany oparty na cięciwie 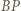 przystaje do kąta między tą cięciwą a styczną w punkcie
przystaje do kąta między tą cięciwą a styczną w punkcie 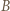 :
: 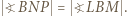 W połączeniu z oczywistą równością
W połączeniu z oczywistą równością 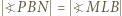 daje to podobieństwo trójkątów
daje to podobieństwo trójkątów 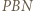 i
i 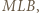 więc i proporcję
więc i proporcję 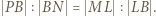 Przy oznaczeniach
Przy oznaczeniach 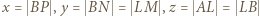 uzyskana proporcja pokazuje, że
uzyskana proporcja pokazuje, że 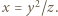 Oznaczając dalej
Oznaczając dalej 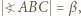 dostajemy ciąg zależności
dostajemy ciąg zależności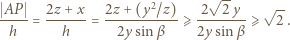
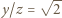 oraz
oraz 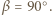 Nierówność
Nierówność 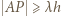 zachodzi więc dla wartości
zachodzi więc dla wartości 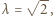 której powiększyć już nie można.
której powiększyć już nie można.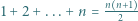 i
i 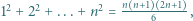 wyprowadzić wzór na
wyprowadzić wzór na 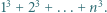
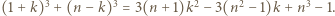
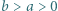 zachodzi nierówność
zachodzi nierówność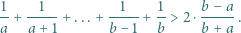
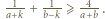
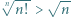 dla naturalnych
dla naturalnych 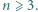
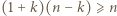 dla
dla 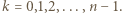 Ponadto dla
Ponadto dla 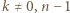 nierówność jest ostra.
nierówność jest ostra. zachodzą następujące równości:
zachodzą następujące równości: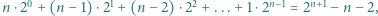
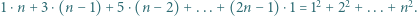
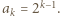
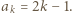 Przyda się też równość
Przyda się też równość 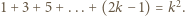
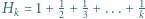 dla całkowitych dodatnich
dla całkowitych dodatnich 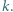 Udowodnić, że
Udowodnić, że 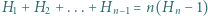 dla naturalnych
dla naturalnych 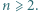
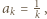 gdzie
gdzie 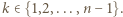
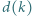 oznacza liczbę dzielników liczby naturalnej
oznacza liczbę dzielników liczby naturalnej 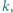 zaś
zaś 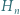 - jak w poprzednim zadaniu. Dowieść, że
- jak w poprzednim zadaniu. Dowieść, że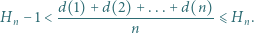
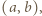 dla których
dla których 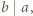 gdzie
gdzie 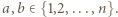 Po sporządzeniu tabeli w kolumnach mamy kolejno
Po sporządzeniu tabeli w kolumnach mamy kolejno 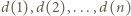 par, a w wierszach
par, a w wierszach 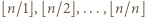 par. Trzeba jeszcze zastosować nierówność
par. Trzeba jeszcze zastosować nierówność