Środek ciężkości II»Zadanie 2
o zadaniu...
- Zadanie pochodzi z artykułu Środek ciężkości II
- Publikacja w Delcie: grudzień 2011
- Publikacja elektroniczna: 01-12-2011
- Artykuł źródłowy w wersji do druku [application/pdf]: (105 KB)
Wykaż, że w dowolnym czworokącie odcinki łączące środki przeciwległych boków oraz odcinek łączący środki przekątnych przecinają się w jednym punkcie.
Czworokąt
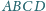 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku
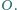 Przekątne
Przekątne
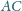 i
i
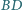 są prostopadłe i przecinają się w punkcie
są prostopadłe i przecinają się w punkcie
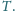 Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
Udowodnij, że punkt przecięcia odcinków łączących środki
przeciwległych boków jest środkiem odcinka
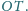
Punkty
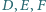 należą odpowiednio do boków
należą odpowiednio do boków
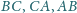 trójkąta
trójkąta
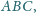 proste
proste
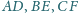 przecinają się w punkcie
przecinają się w punkcie
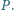 Wykaż,
że
Wykaż,
że
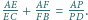
Udowodnij, że w dowolnym czworościanie odcinki łączące środki przeciwległych krawędzi przecinają się w jednym punkcie.
Okrąg
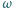 jest wpisany w romb
jest wpisany w romb
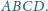 Prosta
Prosta
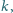 styczna do
okręgu
styczna do
okręgu
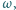 przecina odcinki
przecina odcinki
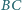 i
i
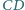 odpowiednio
w punktach
odpowiednio
w punktach
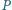 i
i
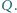 Wykaż, że wartość iloczynu
Wykaż, że wartość iloczynu
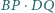 nie zależy od wyboru stycznej
nie zależy od wyboru stycznej
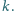
Na przyjęciu spotkało się
 osób. Okazało się, że żadnych
dwóch znajomych nie ma wspólnego znajomego. Ponadto każdych
dwóch nieznajomych ma dokładnie dwóch wspólnych znajomych.
Udowodnij, że wszystkie osoby obecne na tym przyjęciu mają taką samą liczbę
znajomych.
osób. Okazało się, że żadnych
dwóch znajomych nie ma wspólnego znajomego. Ponadto każdych
dwóch nieznajomych ma dokładnie dwóch wspólnych znajomych.
Udowodnij, że wszystkie osoby obecne na tym przyjęciu mają taką samą liczbę
znajomych.

Bolek i Lolek grają w następujący wariant gry w czekoladę (por. artykuł
Wojciecha Czerwińskiego Zagrajmy w czekoladę): tabliczka ma wymiary
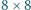 , jedna kostka jest zatruta (Rys. 2), w każdym ruchu gracz łamie
tabliczkę wzdłuż linii i zjada jedną z dwóch otrzymanych części. Przegrywa
ten, kto zje zatrutą kostkę. Grę rozpoczyna Bolek. Czy istnieje takie położenie
zatrutego pola, przy którym Bolek ma strategię wygrywającą?
, jedna kostka jest zatruta (Rys. 2), w każdym ruchu gracz łamie
tabliczkę wzdłuż linii i zjada jedną z dwóch otrzymanych części. Przegrywa
ten, kto zje zatrutą kostkę. Grę rozpoczyna Bolek. Czy istnieje takie położenie
zatrutego pola, przy którym Bolek ma strategię wygrywającą?
Udowodnić, że dla każdej liczby całkowitej dodatniej
 liczba
liczba
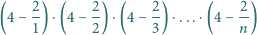
jest całkowita.
Czy dla dowolnego punktu
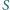 wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
wewnątrz trójkąta można w jego
wierzchołkach umieścić takie masy, by ich środek ciężkości był w
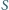 ?
?
Na płaszczyźnie danych jest sześć punktów, z których żadne trzy nie są
współliniowe. Środek ciężkości trójkąta utworzonego przez pewne trzy
z nich oznaczmy jako
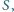 zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
zaś środek ciężkości trójkąta utworzonego
przez pozostałe trzy – jako
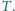 Wykaż, że wszystkie tak wyznaczone
proste
Wykaż, że wszystkie tak wyznaczone
proste
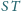 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Udowodnij, że w dowolnym czworościanie odcinki łączące wierzchołki ze środkami ciężkości przeciwległych ścian przecinają się w jednym punkcie.
Wykaż, że wszystkie osie symetrii wielokąta przecinają się w jednym punkcie.
Trzy muchy o równych masach i zaniedbywalnych rozmiarach spacerują po obwodzie trójkąta, jedna z nich przeszła cały obwód. Wykaż, że jeśli środek ciężkości much nie zmienia położenia, to pokrywa się ze środkiem ciężkości trójkąta.
Czy istnieje wielościan wypukły, w którym żaden rzut środka ciężkości na płaszczyznę zawierającą ścianę nie należy do tej ściany?
Wykaż, że środkowe trójkąta przecinają się w środku ciężkości jego wierzchołków.
Udowodnij, że środkiem ciężkości obwodu trójkąta jest środek okręgu wpisanego w trójkąt utworzony przez środki jego boków.
W wierzchołkach trójkąta ostrokątnego
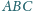 umieszczono masy
odpowiednio
umieszczono masy
odpowiednio
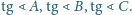 Wykaż, że ich środkiem
ciężkości jest ortocentrum
Wykaż, że ich środkiem
ciężkości jest ortocentrum
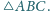
Zadanie zaproponował pan Tomasz Tkocz z Warszawy.
W trójkącie ostrokątnym o bokach długości
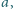
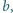
 środkowa
poprowadzona do boku
środkowa
poprowadzona do boku
 ma długość
ma długość
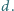 Wykazać, że dla
każdej liczby dodatniej
Wykazać, że dla
każdej liczby dodatniej
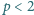 zachodzi nierówność
zachodzi nierówność

Niech
 będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
będzie liczbą naturalną większą od 2. Dowieść, że ze zbioru
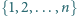 można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.
można usunąć dwie liczby tak, by suma liczb, które
pozostały, była kwadratem liczby naturalnej.
Dany jest prostopadłościan o podstawach
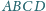 i
i
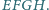 Płaszczyzna
przecina jego krawędzie boczne
Płaszczyzna
przecina jego krawędzie boczne
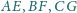 i
i
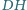 odpowiednio
w punktach
odpowiednio
w punktach
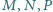 i
i
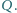 Wykaż, że
Wykaż, że

Liczby
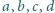 są liczbami rzeczywistymi dodatnimi. Wykaż, że
wśród liczb:
są liczbami rzeczywistymi dodatnimi. Wykaż, że
wśród liczb:

co najmniej dwie są dodatnie.
W przestrzeni dane są takie punkty
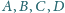 , że
, że
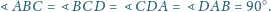
Udowodnić, że punkty
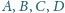 leżą na jednej płaszczyźnie.
leżą na jednej płaszczyźnie.
Udowodnić, że jeśli
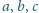 są długościami boków trójkąta, to
zachodzi nierówność
są długościami boków trójkąta, to
zachodzi nierówność
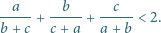
Udowodnić, że spośród dowolnych pięciu liczb całkowitych (niekoniecznie różnych) można wybrać trzy, których suma jest podzielna przez 3.
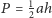
Punkt
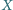 leży wewnątrz sześciokąta wypukłego
leży wewnątrz sześciokąta wypukłego
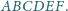 Punkty
Punkty
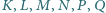 są odpowiednio
środkami boków
są odpowiednio
środkami boków
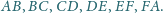 Wykaż, że
Wykaż, że
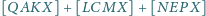 nie zależy od wyboru punktu
nie zależy od wyboru punktu
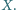
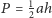
Dany jest czworokąt wypukły
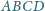 o polu 1. Punkt
o polu 1. Punkt
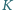 jest
symetryczny do punktu
jest
symetryczny do punktu
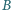 względem punktu
względem punktu
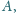 punkt
punkt
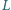 jest
symetryczny do punktu
jest
symetryczny do punktu
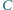 względem punktu
względem punktu
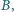 punkt
punkt
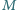 jest symetryczny do punktu
jest symetryczny do punktu
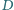 względem punktu
względem punktu
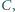 punkt
punkt
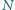 jest symetryczny do punktu
jest symetryczny do punktu
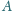 względem
punktu
względem
punktu
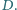 Oblicz
Oblicz