Identyczne rysunki»Zadanie 3
o zadaniu...
- Zadanie pochodzi z artykułu Identyczne rysunki
- Publikacja w Delcie: sierpień 2013
- Publikacja elektroniczna: 31-07-2013
- Artykuł źródłowy w wersji do druku [application/pdf]: (83 KB)
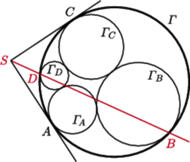
Okręgi
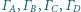 są styczne wewnętrznie do okręgu
są styczne wewnętrznie do okręgu
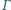 odpowiednio
w punktach
odpowiednio
w punktach
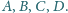 Ponadto okręgi
Ponadto okręgi
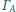 i
i
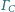 są styczne
zewnętrznie do obu okręgów
są styczne
zewnętrznie do obu okręgów
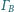 i
i
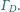 Proste styczne do
okręgu
Proste styczne do
okręgu
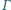 w punktach
w punktach
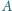 i
i
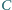 przecinają się w punkcie
przecinają się w punkcie
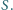 Udowodnij, że punkty
Udowodnij, że punkty
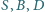 leżą na jednej prostej.
leżą na jednej prostej.
 i promieniu
i promieniu
 okręgi
okręgi
 i
i
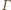 są stałe. Stąd
są stałe. Stąd
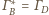 oraz
oraz
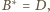 co daje
tezę.
co daje
tezę.
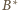 zamiast
zamiast
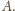
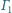 i
i
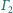 są styczne zewnętrznie i styczne do prostej
są styczne zewnętrznie i styczne do prostej
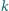 odpowiednio w punktach
odpowiednio w punktach
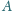 i
i
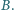 Odcinek
Odcinek
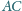 jest
średnicą okręgu
jest
średnicą okręgu
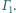 Prosta
Prosta
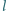 przechodzi przez punkt
przechodzi przez punkt
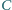 i jest styczna do okręgu
i jest styczna do okręgu
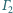 w punkcie
w punkcie
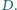 Wykaż, że
Wykaż, że
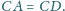
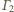 jest stały przy inwersji względem
jest stały przy inwersji względem
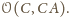


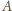 oznacza podzbiór wszystkich pokolorowanych punktów
na okręgu, zaś
oznacza podzbiór wszystkich pokolorowanych punktów
na okręgu, zaś
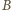 niech oznacza podzbiór wszystkich tych
punktów, których antypody są pokolorowane. Chcemy udowodnić, że
niech oznacza podzbiór wszystkich tych
punktów, których antypody są pokolorowane. Chcemy udowodnić, że
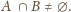 Załóżmy przeciwnie, że są rozłączne. W tej sytuacji
Załóżmy przeciwnie, że są rozłączne. W tej sytuacji
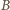 składa się z odcinków o łącznej długości takiej jak
składa się z odcinków o łącznej długości takiej jak
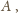 więc
łączna długość odcinków składających się na sumę
więc
łączna długość odcinków składających się na sumę
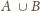 jest większa
niż obwód okręgu, co daje sprzeczność.
jest większa
niż obwód okręgu, co daje sprzeczność.
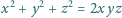
 to liczby całkowite dodatnie, takie
że
to liczby całkowite dodatnie, takie
że
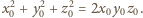 Ponieważ prawa strona jest liczbą parzystą, to
dokładnie dwie z liczb
Ponieważ prawa strona jest liczbą parzystą, to
dokładnie dwie z liczb
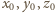 są nieparzyste lub żadna nieparzysta nie
jest. Pierwszy przypadek nie może mieć miejsca, gdyż wówczas lewa strona
przy dzieleniu przez
są nieparzyste lub żadna nieparzysta nie
jest. Pierwszy przypadek nie może mieć miejsca, gdyż wówczas lewa strona
przy dzieleniu przez
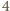 dałaby resztę
dałaby resztę
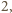 zaś prawa
zaś prawa
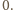 Dlatego
Dlatego
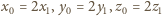 dla pewnych liczb całkowitych dodatnich
dla pewnych liczb całkowitych dodatnich
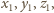 mniejszych od
mniejszych od
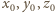 odpowiednio. Po wstawieniu do
równania otrzymujemy zależność
odpowiednio. Po wstawieniu do
równania otrzymujemy zależność
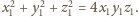 Powtarzając
całe rozumowanie, dostajemy malejące ciągi liczb całkowitych dodatnich
Powtarzając
całe rozumowanie, dostajemy malejące ciągi liczb całkowitych dodatnich
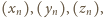 przy czym
przy czym
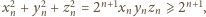 co jest
niemożliwe.
co jest
niemożliwe.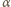 oraz prawdziwa jest implikacja
oraz prawdziwa jest implikacja
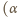 to
to
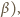 to
prawdziwe jest też zdanie
to
prawdziwe jest też zdanie
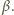 Można sobie przecież wyobrazić, że
długość dowodu formuły
Można sobie przecież wyobrazić, że
długość dowodu formuły
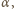 jak i długość dowodu implikacji
jak i długość dowodu implikacji
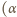 to
to
 są dostępnymi liczbami naturalnymi, a ich suma już
nie.
są dostępnymi liczbami naturalnymi, a ich suma już
nie.
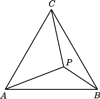
 wewnątrz trójkąta równobocznego
wewnątrz trójkąta równobocznego
 Udowodnić, że
Udowodnić, że
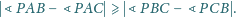
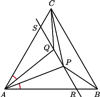
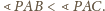 Odbijmy
symetrycznie
Odbijmy
symetrycznie
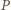 względem dwusiecznej kąta
względem dwusiecznej kąta
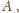 otrzymując punkt
otrzymując punkt
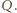 Niech
Niech
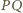 przecina
przecina
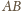 i
i
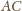 odpowiednio
w punktach
odpowiednio
w punktach
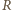 i
i
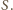 Oczywiście
Oczywiście
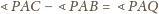
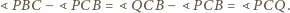
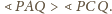 Rozważmy obraz
Rozważmy obraz
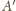 punktu
punktu
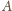 przy symetrii względem
przy symetrii względem
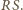 Zauważmy, że punkt
Zauważmy, że punkt
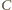 leży na zewnątrz okręgu opisanego na trójkącie równobocznym
leży na zewnątrz okręgu opisanego na trójkącie równobocznym
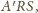 gdyż
gdyż
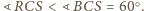 W szczególności, punkt
W szczególności, punkt
 leży na zewnątrz okręgu opisanego na trójkącie
leży na zewnątrz okręgu opisanego na trójkącie
 gdyż
ten okrąg leży wewnątrz poprzedniego. Stąd
gdyż
ten okrąg leży wewnątrz poprzedniego. Stąd
 -ty kamień?
-ty kamień?
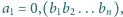 w której zapisie
dziesiętnym blok cyfr
w której zapisie
dziesiętnym blok cyfr
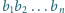 powtarza się okresowo po przecinku.
Rozważmy liczby
powtarza się okresowo po przecinku.
Rozważmy liczby
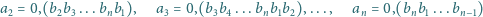
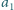 przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
przez cykliczne przesunięcia cyfr w bloku. Udowodnić,
że
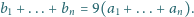
 dla
dla
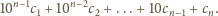
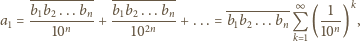
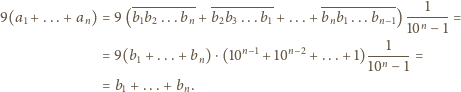
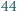 rycerzy. Wiadomo, że każdy rycerz ma
wśród pozostałych co najwyżej
rycerzy. Wiadomo, że każdy rycerz ma
wśród pozostałych co najwyżej
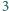 wrogów (zakładamy, że jeśli
rycerz
wrogów (zakładamy, że jeśli
rycerz
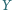 jest wrogiem rycerza
jest wrogiem rycerza
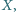 to i
to i
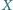 jest wrogiem
rycerza
jest wrogiem
rycerza
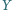 ). Udowodnić, że można tak rozsadzić rycerzy przy dwóch
stołach (dowolnie dużych), by każdy rycerz siedział przy stole z co najwyżej
jednym ze swoich wrogów.
). Udowodnić, że można tak rozsadzić rycerzy przy dwóch
stołach (dowolnie dużych), by każdy rycerz siedział przy stole z co najwyżej
jednym ze swoich wrogów.
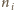 oznacza liczbę wrogów
oznacza liczbę wrogów
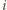 -tego rycerza, którzy zasiadają
z nim przy stole. W kroku 0 posadźmy wszystkich rycerzy przy pierwszym
stole. Będziemy w kolejnych krokach przesadzać rycerzy, rozważając
liczbę
-tego rycerza, którzy zasiadają
z nim przy stole. W kroku 0 posadźmy wszystkich rycerzy przy pierwszym
stole. Będziemy w kolejnych krokach przesadzać rycerzy, rozważając
liczbę
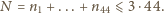
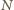 zmienia się na
zmienia się na
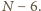 Jeśli zaś
siedział on przy stole wraz z dwoma wrogami, to
Jeśli zaś
siedział on przy stole wraz z dwoma wrogami, to
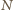 zmienia się na
liczbę niewiększą niż
zmienia się na
liczbę niewiększą niż
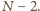 Skoro po wykonaniu każdego kroku
Skoro po wykonaniu każdego kroku
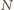 maleje, to wykonamy ich skończenie wiele. Oczywiście, po
wykonaniu ostatniego kroku
maleje, to wykonamy ich skończenie wiele. Oczywiście, po
wykonaniu ostatniego kroku
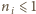 dla każdego
dla każdego
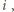 co kończy
dowód.
co kończy
dowód.
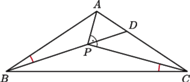
 trójkąta równoramiennego
trójkąta równoramiennego
 o podstawie
o podstawie
 dany jest punkt
dany jest punkt
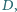 przy czym
przy czym
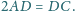 Na odcinku
Na odcinku
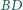 dany jest taki punkt
dany jest taki punkt
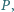 że kąt
że kąt
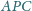 jest prosty.
Udowodnić, że kąty
jest prosty.
Udowodnić, że kąty
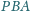 i
i
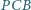 są równe.
są równe.
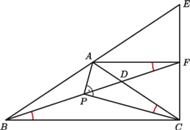
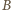 względem
względem
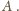 Otrzymany
punkt nazwijmy
Otrzymany
punkt nazwijmy
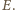 Odcinek
Odcinek
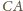 jest środkową trójkąta
jest środkową trójkąta
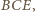 a ponieważ
a ponieważ
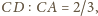 więc
więc
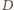 jest
środkiem ciężkości tego trójkąta. Niech
jest
środkiem ciężkości tego trójkąta. Niech
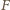 oznacza środek boku
oznacza środek boku
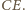 Leży on na przedłużeniu odcinka
Leży on na przedłużeniu odcinka
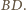 Ponieważ
Ponieważ
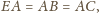 więc kąt
więc kąt
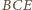 jest prosty, a zatem również kąt
jest prosty, a zatem również kąt
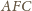 jest prosty. Stąd punkty
jest prosty. Stąd punkty
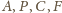 leżą na okręgu o średnicy
leżą na okręgu o średnicy
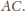 Wobec tego
Wobec tego
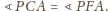 Ale
Ale
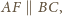 więc
więc
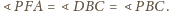
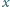 spełnia równanie
spełnia równanie
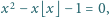 to każda potęga liczby
to każda potęga liczby
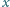 o wykładniku
dodatnim nieparzystym także spełnia to równanie.
o wykładniku
dodatnim nieparzystym także spełnia to równanie.
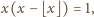 to
to
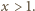 Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
Wykażemy indukcyjnie, że dla
każdej liczby nieparzystej
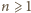 różnica
różnica
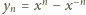 jest liczbą
całkowitą.
jest liczbą
całkowitą.
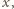 widzimy, że
widzimy, że
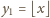 (liczba całkowita). Zatem także liczba
(liczba całkowita). Zatem także liczba
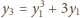 jest całkowita.
jest całkowita.
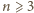 i załóżmy, że liczby
i załóżmy, że liczby
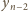 oraz
oraz
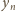 są całkowite. Przekształcenie
są całkowite. Przekształcenie
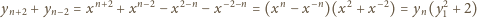
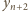 też jest całkowita. Przez indukcję
wnosimy, że liczby
też jest całkowita. Przez indukcję
wnosimy, że liczby
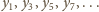 wszystkie są całkowite.
wszystkie są całkowite.
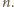 Ze związków
Ze związków
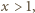
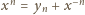 (
(
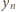 całkowite) wynika, że
całkowite) wynika, że
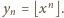 Zachodzi
więc równość
Zachodzi
więc równość
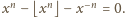 Wystarczy ją pomnożyć przez
Wystarczy ją pomnożyć przez
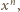 by uzyskać tezę zadania.
by uzyskać tezę zadania.
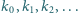 taki, że dla każdego
taki, że dla każdego
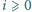 iloczyn
iloczyn
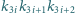 jest
podzielny przez każdą z liczb
jest
podzielny przez każdą z liczb
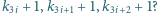
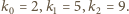 Przyjmijmy, że wyrazy
Przyjmijmy, że wyrazy
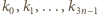 są
już określone i tworzą ciąg rosnący długości
są
już określone i tworzą ciąg rosnący długości
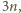 spełniający
wymagany warunek. Oznaczmy dla wygody:
spełniający
wymagany warunek. Oznaczmy dla wygody:
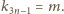 Określamy
kolejne trzy wyrazy:
Określamy
kolejne trzy wyrazy:
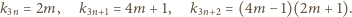
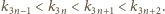 Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
Pozostaje sprawdzić, że iloczyn
trzech wypisanych liczb, równy
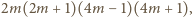 dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
dzieli się
przez każdą z tych liczb, powiększoną o 1, czyli przez liczby
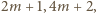
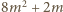 ; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
; a to jest oczywiste. Kontynuując, otrzymujemy nieskończony
ciąg
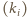 o żądanych własnościach.
o żądanych własnościach.
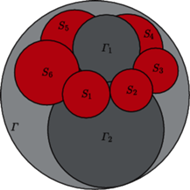
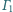 i
i
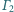 są styczne wewnętrznie do sfery
są styczne wewnętrznie do sfery
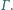 Do każdej z tych trzech sfer styczna jest każda z
Do każdej z tych trzech sfer styczna jest każda z
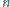 sfer
sfer
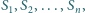 ponadto dla każdego
ponadto dla każdego
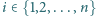 sfera
sfera
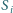 styczna jest do sfery
styczna jest do sfery
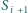 (przy czym
(przy czym
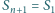 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch sfer
istnieje taki łańcuch sfer
 W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
W jaki sposób zależy to od
rozmiarów i wzajemnego położenia sfer
 Czy i jak zależy to
od wyboru początkowej sfery
Czy i jak zależy to
od wyboru początkowej sfery
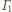 i
i
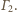 Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
Wówczas obrazami tych dwóch sfer, przechodzących
przez środek inwersji, są płaszczyzny
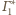 i
i
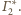 Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
Płaszczyzny te są
równoległe, bo jedynym wspólnym punktem sfer
 i
i
 jest
środek inwersji.
jest
środek inwersji.
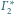
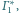
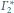
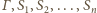 jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
jest sfera (bo żadna
z nich nie przechodzi przez środek inwersji) styczna do
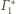 i
i
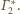 Z równoległości tych płaszczyzn wynika, że wszystkie sfery
Z równoległości tych płaszczyzn wynika, że wszystkie sfery
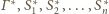 mają średnice równe odległości
mają średnice równe odległości
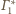 od
od
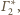 czyli są przystające. Ponadto wszystkie sfery
czyli są przystające. Ponadto wszystkie sfery
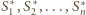 są
styczne do sfery
są
styczne do sfery
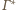 oraz dla każdego
oraz dla każdego
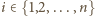 sfera
sfera
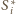 styczna jest do sfery
styczna jest do sfery
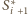 (przy czym
(przy czym
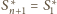 ).
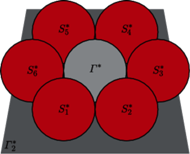
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
).
Odpowiada to sytuacji, gdy na stole (płaszczyźnie
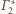 ) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
) ustawiamy piłeczki,
przy czym łańcuch kolejno stycznych piłeczek
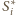 otacza środkową
piłeczkę
otacza środkową
piłeczkę
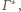 stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
stykając się także z nią. Skoro wszystkie piłeczki są tej
samej wielkości, to taki łańcuch „domyka” się wtedy i tylko wtedy, gdy
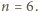
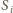 ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
ma zawsze dokładnie sześć elementów i nie zależy to od
rozmiarów ani położenia sfer
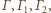 ani też od wyboru sfery
ani też od wyboru sfery
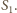 Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
Taki łańcuch sfer nazywa się Hexletem Soddy’ego.
 Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
Pozostaje pytanie, gdzie po inwersji „ukryła się” cała
asymetria wyjściowej sytuacji? Otóż jest ona „zakodowana” w położeniu
środka inwersji wewnątrz sfery
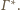
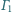 i
i
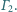 Do
każdego z nich styczny jest każdy z
Do
każdego z nich styczny jest każdy z
 okręgów
okręgów
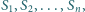 ponadto
dla każdego
ponadto
dla każdego
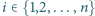 okrąg
okrąg
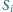 styczny jest do okręgu
styczny jest do okręgu
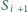 (przy czym
(przy czym
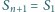 ). Dla jakich
). Dla jakich
 istnieje taki łańcuch
okręgów
istnieje taki łańcuch
okręgów
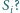 W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
W jaki sposób zależy to od rozmiarów i wzajemnego
położenia okręgów
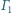 i
i
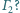 Czy i jak zależy to od wyboru
początkowego okręgu
Czy i jak zależy to od wyboru
początkowego okręgu
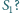
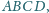 w którym
w którym
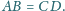 Ponadto
suma pól ścian
Ponadto
suma pól ścian
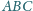 i
i
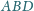 jest równa sumie pól
ścian
jest równa sumie pól
ścian
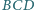 i
i
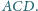 Dowieść, że
Dowieść, że
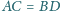 lub
lub
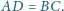
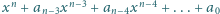 ma współczynniki
rzeczywiste
ma współczynniki
rzeczywiste
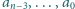 nie wszystkie równe
nie wszystkie równe
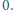 Udowodnić, że
ma on mniej niż
Udowodnić, że
ma on mniej niż
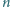 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
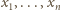 to pierwiastki rzeczywiste naszego
wielomianu. Wówczas
to pierwiastki rzeczywiste naszego
wielomianu. Wówczas
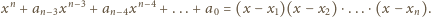
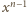 i
i
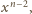 dostajemy
dostajemy
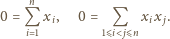
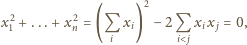
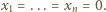 Zatem
Zatem
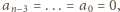 co jest sprzeczne
z założeniem.
co jest sprzeczne
z założeniem.
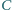 o następującej własności: jeśli
równanie
o następującej własności: jeśli
równanie
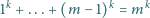
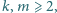 to
to
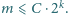
 nie może być zbyt duże. Do dziś pozostaje
otwartym problemem hipoteza Erdősa, że to równanie nie ma rozwiązań
(zob. również zadanie M 1374, Delta 1(464)/2013).
nie może być zbyt duże. Do dziś pozostaje
otwartym problemem hipoteza Erdősa, że to równanie nie ma rozwiązań
(zob. również zadanie M 1374, Delta 1(464)/2013).
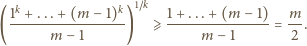
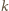 i
i
 spełniają podane równanie, dostajemy
spełniają podane równanie, dostajemy
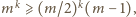 a stąd
a stąd
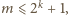 co jest mniejsze niż
co jest mniejsze niż
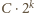 np. dla
np. dla
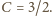
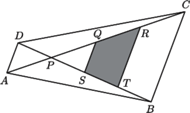
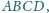 którego przekątne przecinają się
w punkcie
którego przekątne przecinają się
w punkcie
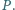 Na przekątnej
Na przekątnej
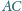 dane są jeszcze punkty
dane są jeszcze punkty
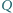 i
i
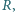 dzielące ją wraz z
dzielące ją wraz z
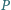 na cztery równe części, tzn.
na cztery równe części, tzn.
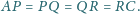 Na przekątnej
Na przekątnej
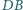 dane są jeszcze punkty
dane są jeszcze punkty
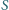 i
i
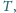 które wraz z
które wraz z
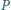 dzielą ją na cztery równe części,
tzn.
dzielą ją na cztery równe części,
tzn.
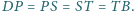 Obliczyć stosunek pól czworokątów
Obliczyć stosunek pól czworokątów
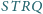 i
i
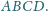
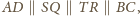 więc
więc
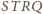 i
i
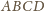 są trapezami o stosunku wysokości
są trapezami o stosunku wysokości
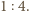
 oznaczmy długość odcinka
oznaczmy długość odcinka
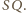 Wówczas
Wówczas
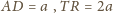 oraz
oraz
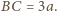 Zatem
Zatem
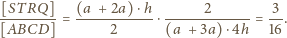
 jest określony wzorem rekurencyjnym
jest określony wzorem rekurencyjnym
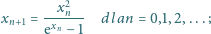
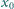 jest dowolną liczbą dodatnią. Obliczyć
granicę
jest dowolną liczbą dodatnią. Obliczyć
granicę
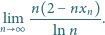
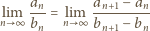
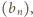 rosnącego do nieskończoności, i dla każdego
ciągu
rosnącego do nieskończoności, i dla każdego
ciągu
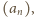 dla którego granica po prawej stronie istnieje.
dla którego granica po prawej stronie istnieje.
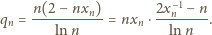
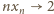 ; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
; pozostaje zająć się
drugim czynnikiem. We wzorze Stolza przyjmijmy
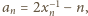
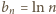 :
:
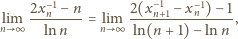
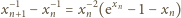
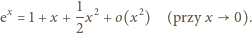
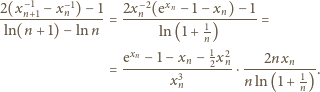
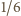 (nieco
dłuższy fragment rozwinięcia
(nieco
dłuższy fragment rozwinięcia
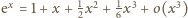 ).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
).
Drugi czynnik: licznik dąży do 4, mianownik do 1. Cały iloczyn dąży do
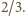 Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
Tyle więc wynosi granica napisana po lewej stronie równości (2).
Wracamy do równości (1), pamiętając, że
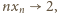 i otrzymujemy
ostatecznie
i otrzymujemy
ostatecznie
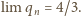
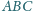 oraz punkt
oraz punkt
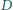 na
boku
na
boku
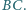 Punkty
Punkty
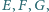 leżące odpowiednio na bokach
leżące odpowiednio na bokach
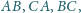 są wyznaczone przez warunki
są wyznaczone przez warunki
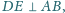
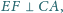
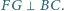 Proste
Proste
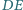 i
i
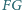 przecinają się
w punkcie
przecinają się
w punkcie
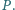 W jakim stosunku prosta
W jakim stosunku prosta
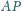 dzieli odcinek
dzieli odcinek
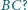
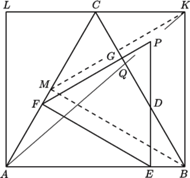
 tak, by punkt
tak, by punkt
 był środkiem
odcinka
był środkiem
odcinka
 Niech
Niech
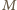 będzie środkiem boku
będzie środkiem boku
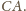 Każdy
z trójkątów
Każdy
z trójkątów
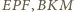 ma boki prostopadłe do odpowiednich boków
trójkąta
ma boki prostopadłe do odpowiednich boków
trójkąta
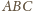 (rysunek); są to więc trójkąty o bokach odpowiednio
równoległych – zatem jednokładne. Środkiem jednokładności jest punkt
(rysunek); są to więc trójkąty o bokach odpowiednio
równoległych – zatem jednokładne. Środkiem jednokładności jest punkt
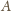 (współliniowy z
(współliniowy z
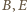 oraz z
oraz z
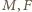 ). Punktowi
). Punktowi
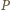 odpowiada w tej jednokładności punkt
odpowiada w tej jednokładności punkt
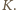 To znaczy, że
prosta
To znaczy, że
prosta
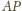 przechodzi przez
przechodzi przez
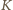 (niezależnie od wyboru
początkowego punktu
(niezależnie od wyboru
początkowego punktu
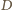 ) i przecina odcinek
) i przecina odcinek
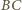 w takim punkcie
w takim punkcie
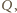 że trójkąty
że trójkąty
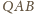 i
i
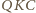 są podobne. Stąd wynik:
są podobne. Stąd wynik:
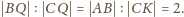
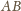 kwadratu to część prostej
kwadratu to część prostej
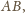 zawarta w kącie
zawarta w kącie
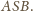
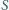 i wpisany w czworokąt wypukły
i wpisany w czworokąt wypukły
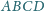 jest styczny do boków
jest styczny do boków
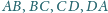 odpowiednio
w punktach
odpowiednio
w punktach
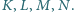 Proste
Proste
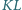 i
i
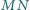 przecinają
się w punkcie
przecinają
się w punkcie
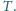 Wykaż, że proste
Wykaż, że proste
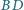 i
i
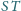 są
prostopadłe.
są
prostopadłe.

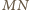 w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
w inwersji względem danego okręgu
jest okrąg przechodzący przez środek inwersji
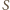 i przez stałe
punkty
i przez stałe
punkty
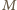 i
i
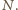 Leży na nim też punkt
Leży na nim też punkt
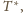 bo
punkt
bo
punkt
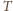 leży na prostej
leży na prostej
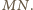 Średnicą tego okręgu jest
Średnicą tego okręgu jest
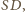 ponieważ kąty
ponieważ kąty
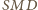 i
i
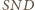 są proste, stąd także
są proste, stąd także
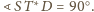
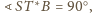 więc
więc
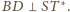 Z definicji inwersji
punkty
Z definicji inwersji
punkty
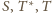 są współliniowe, co kończy dowód.
są współliniowe, co kończy dowód.

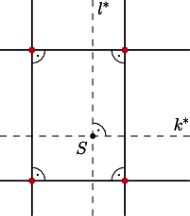
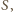 przy oznaczeniach jak na rysunku. Proste
przy oznaczeniach jak na rysunku. Proste
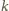 i
i
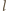 są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
są stałe
przy tej inwersji. Obrazem każdego z okręgów, przechodzącego przez środek
inwersji, jest prosta równoległa odpowiednio do
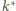 lub
lub
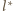 (okrąg
styczny do prostej
(okrąg
styczny do prostej
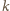 lub
lub
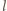 mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
mieści się w półpłaszczyźnie przez
nią wyznaczonej, więc jego obraz też, rysunek obok). Zatem obrazami
kolorowych punktów są wierzchołki prostokąta. Leżą one na okręgu
nieprzechodzącym przez środek inwersji (bo środek ten jest wewnątrz
prostokąta), więc także przed inwersją kolorowe punkty leżą na jednym
okręgu.
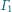 i
i
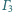 jest styczny zewnętrznie
do każdego z rozłącznych okręgów
jest styczny zewnętrznie
do każdego z rozłącznych okręgów
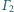 i
i
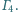 Wykaż, że punkty
styczności leżą na jednym okręgu.
Wykaż, że punkty
styczności leżą na jednym okręgu.
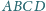 okręgi wpisane w trójkąty
okręgi wpisane w trójkąty
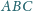 i
i
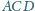 są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
są styczne. Wykaż, że ich punkty styczności
z bokami czworokąta leżą na jednym okręgu.
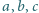 jest spełniona
nierówność
jest spełniona
nierówność
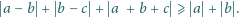
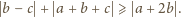
 i wystarczy teraz udowodnić,
że
i wystarczy teraz udowodnić,
że
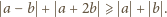
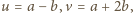 tzn.
tzn.
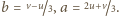 Otrzymujemy wówczas
Otrzymujemy wówczas
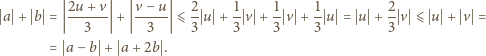
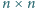 parami różnych liczb rzeczywistych.
Udowodnić, że można w niej zaznaczyć
parami różnych liczb rzeczywistych.
Udowodnić, że można w niej zaznaczyć
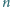 liczb, po jednej
w każdym wierszu i kolumnie, w taki sposób, że jeśli w pewnym wierszu
zaznaczona liczba jest większa od jakieś innej w tym wierszu, to ta druga liczba
jest mniejsza od zaznaczonej liczby z jej kolumny.
liczb, po jednej
w każdym wierszu i kolumnie, w taki sposób, że jeśli w pewnym wierszu
zaznaczona liczba jest większa od jakieś innej w tym wierszu, to ta druga liczba
jest mniejsza od zaznaczonej liczby z jej kolumny.
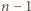 razy, więc
wykonamy co najwyżej
razy, więc
wykonamy co najwyżej
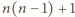 kroków. Po ostatnim kroku
w każdej kolumnie będzie zaznaczony dokładnie jeden element.
kroków. Po ostatnim kroku
w każdej kolumnie będzie zaznaczony dokładnie jeden element.
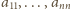 (możemy tak założyć, ewentualnie przestawiając
kolumny). Spójrzmy na
(możemy tak założyć, ewentualnie przestawiając
kolumny). Spójrzmy na
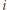 -ty wiersz. Jeśli
-ty wiersz. Jeśli
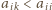 dla pewnego
dla pewnego
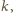 to znaczy, że w pewnym kroku liczba
to znaczy, że w pewnym kroku liczba
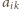 była odznaczona,
a zatem
była odznaczona,
a zatem
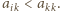
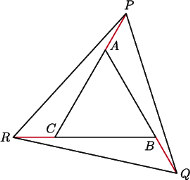
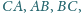 będących przedłużeniami boków
trójkąta
będących przedłużeniami boków
trójkąta
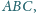 obrano odpowiednio punkty
obrano odpowiednio punkty
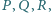 przy czym
przy czym
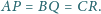 Udowodnić, że jeśli trójkąt
Udowodnić, że jeśli trójkąt
 jest
równoboczny, to trójkąt
jest
równoboczny, to trójkąt
 również.
również.
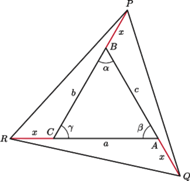
 jak na rysunku
i załóżmy, że
jak na rysunku
i załóżmy, że
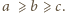
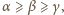 a stąd
a stąd
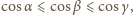 ponieważ
funkcja
ponieważ
funkcja
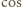 jest malejąca na przedziale
jest malejąca na przedziale
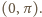 Przyjmijmy,
że
Przyjmijmy,
że
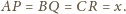 Wówczas z twierdzenia cosinusów
otrzymujemy
Wówczas z twierdzenia cosinusów
otrzymujemy
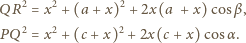
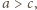 to ponieważ
to ponieważ
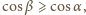 mielibyśmy
mielibyśmy
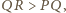 co przeczyłoby założeniu, że trójkąt
co przeczyłoby założeniu, że trójkąt
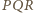 jest
równoboczny. W takim razie
jest
równoboczny. W takim razie
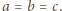
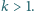 Znaleźć wszystkie liczby naturalne
Znaleźć wszystkie liczby naturalne
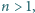 spełniające nierówność
spełniające nierówność

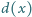 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej

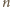 ma co najmniej dwa różne dzielniki pierwsze
ma co najmniej dwa różne dzielniki pierwsze
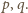 Napiszmy
Napiszmy
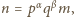 gdzie
gdzie
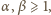 zaś czynnik
zaś czynnik
 jest niepodzielny przez
jest niepodzielny przez
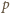 ani
ani
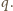 Iloczyn
Iloczyn
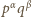 ma
ma
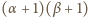 dzielników dodatnich; iloczyn
dzielników dodatnich; iloczyn
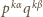 ma
ma
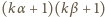 dzielników dodatnich. Zatem
dzielników dodatnich. Zatem
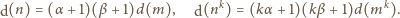
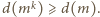 Jeśli więc zachodzi postulowana nierówność
Jeśli więc zachodzi postulowana nierówność
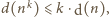 to
to
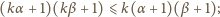
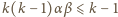 ; a to jest niemożliwe, skoro
; a to jest niemożliwe, skoro
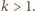
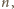 będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
będące potęgami liczb
pierwszych. Każda taka liczba spełnia wymagany warunek; jeśli bowiem
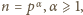 to
to
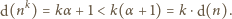
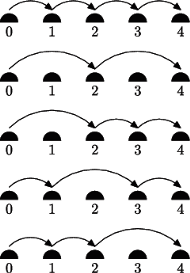
 -kąta foremnego są pokolorowane dwoma kolorami. Co
jednostkę czasu pokolorowanie zmienia się: każdy wierzchołek przyjmuje
kolor, który bezpośrednio przed tym momentem miała większość
z trójki wierzchołków: sam rozważany wierzchołek oraz dwa z nim
sąsiadujące. Proces kończy się, gdy nowe pokolorowanie okaże się identyczne
z poprzednim (tzn. gdy nic się już nie zmienia). Dla każdej liczby naturalnej
-kąta foremnego są pokolorowane dwoma kolorami. Co
jednostkę czasu pokolorowanie zmienia się: każdy wierzchołek przyjmuje
kolor, który bezpośrednio przed tym momentem miała większość
z trójki wierzchołków: sam rozważany wierzchołek oraz dwa z nim
sąsiadujące. Proces kończy się, gdy nowe pokolorowanie okaże się identyczne
z poprzednim (tzn. gdy nic się już nie zmienia). Dla każdej liczby naturalnej
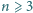 wyjaśnić, dla jakich początkowych konfiguracji kolorów proces
będzie trwał nieskończenie.
wyjaśnić, dla jakich początkowych konfiguracji kolorów proces
będzie trwał nieskończenie.
 parzystych). Wówczas po pierwszym ruchu
wszystkie kolory zmienią się, po drugim powróci sytuacja początkowa, i ten
cykl stale będzie się powtarzał. To jest ta konfiguracja początkowa, o jaką pyta
zadanie.
parzystych). Wówczas po pierwszym ruchu
wszystkie kolory zmienią się, po drugim powróci sytuacja początkowa, i ten
cykl stale będzie się powtarzał. To jest ta konfiguracja początkowa, o jaką pyta
zadanie.