Zadanie ZM-1357
o zadaniu...
- Publikacja w Delcie: sierpień 2012
- Publikacja elektroniczna: 31-07-2012
Udowodnij, że jeśli
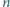 jest dodatnią liczbą całkowitą, to liczba
jest dodatnią liczbą całkowitą, to liczba
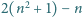 nie jest kwadratem liczby całkowitej.
nie jest kwadratem liczby całkowitej.
Udowodnij, że wśród dowolnych
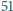 wierzchołków
wierzchołków
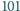 -kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
-kąta
foremnego istnieją takie trzy, które są wierzchołkami trójkąta równoramiennego.
Na polu c1 szachownicy
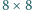 stoi królowa. Gracze na przemian
przesuwają ją o dowolną liczbę pól w prawo, do góry albo po przekątnej
w prawo i do góry. Wygrywa ten, kto postawi królową na polu h8. Który
gracz ma strategię wygrywającą i jaką?
stoi królowa. Gracze na przemian
przesuwają ją o dowolną liczbę pól w prawo, do góry albo po przekątnej
w prawo i do góry. Wygrywa ten, kto postawi królową na polu h8. Który
gracz ma strategię wygrywającą i jaką?
Na stole stoją dwa talerze owoców: na jednym jest 5 jabłek, na drugim 7 pomarańczy. Pojedynczy ruch w grze polega na zabraniu dowolnej liczby owoców z jednego z talerzy lub po tyle samo owoców z każdego z talerzy. Gracze wykonują ruchy na przemian; wygrywa ten, kto zabierze ostatni owoc ze stołu. Który gracz ma strategię wygrywającą i jaką?
Liczby
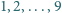 napisano na osobnych kartkach. Gracze na przemian
zabierają sobie po jednej z nich. Wygrywa ten, kto jako pierwszy skompletuje
trzy kartki o sumie liczb równej 15. Gracz rozpoczynający wybrał kartkę z „2”.
Jak powinien postąpić drugi gracz?
napisano na osobnych kartkach. Gracze na przemian
zabierają sobie po jednej z nich. Wygrywa ten, kto jako pierwszy skompletuje
trzy kartki o sumie liczb równej 15. Gracz rozpoczynający wybrał kartkę z „2”.
Jak powinien postąpić drugi gracz?
W trójkącie ostrokątnym
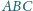 punkt
punkt
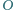 jest środkiem okręgu
opisanego, a dwusieczna kąta
jest środkiem okręgu
opisanego, a dwusieczna kąta
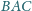 przecina bok
przecina bok
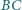 w punkcie
w punkcie
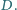 Niech
Niech
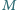 będzie takim punktem, że
będzie takim punktem, że
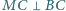 oraz
oraz
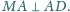 Proste
Proste
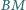 i
i
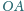 przecinają się w punkcie
przecinają się w punkcie
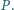 Wykazać, że okrąg o środku
Wykazać, że okrąg o środku
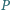 i przechodzący przez punkt
i przechodzący przez punkt
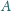 jest styczny do prostej
jest styczny do prostej
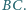
Rozstrzygnąć, czy istnieje taka dodatnia liczba wymierna
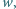 niebędąca
liczbą całkowitą, że potęga
niebędąca
liczbą całkowitą, że potęga
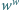 jest liczbą wymierną
jest liczbą wymierną
Niech
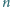 będzie liczbą całkowitą dodatnią. Udowodnić, że liczba
będzie liczbą całkowitą dodatnią. Udowodnić, że liczba
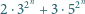
jest podzielna przez
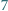 wtedy i tylko wtedy, gdy
wtedy i tylko wtedy, gdy
 jest liczbą
parzystą.
jest liczbą
parzystą.
Niech
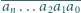 oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
oznacza liczbę, której cyfrą jedności w zapisie
dziesiętnym jest
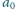 , cyfrą dziesiątek –
, cyfrą dziesiątek –
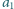 , cyfrą setek –
, cyfrą setek –
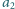 ,
itd. Znaleźć wszystkie liczby czterocyfrowe
,
itd. Znaleźć wszystkie liczby czterocyfrowe
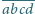 , które spełniają
równość
, które spełniają
równość


Dany jest nierównoramienny trójkąt prostokątny
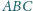 o kącie
prostym przy wierzchołku
o kącie
prostym przy wierzchołku
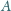 . Niech
. Niech
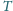 będzie środkiem
okręgu wpisanego, zaś
będzie środkiem
okręgu wpisanego, zaś
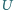 i
i
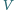 niech będą jego punktami
styczności odpowiednio z bokami
niech będą jego punktami
styczności odpowiednio z bokami
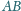 i
i
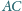 . Prosta
. Prosta
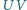 przecina w punkcie
przecina w punkcie
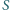 styczną do okręgu opisanego poprowadzoną
w punkcie
styczną do okręgu opisanego poprowadzoną
w punkcie
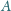 . Udowodnić, że proste
. Udowodnić, że proste
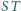 i
i
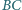 są równoległe.
są równoległe.
Zadanie 644 zaproponował pan Witold Bednarek z Łodzi.
Dana jest liczba rzeczywista
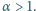 Obliczyć minimalną wartość
funkcji
Obliczyć minimalną wartość
funkcji
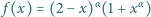
na przedziale
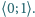
Wyznaczyć wszystkie pary
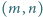 liczb całkowitych
liczb całkowitych
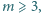
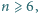 spełniające równanie
spełniające równanie

Udowodnić, że dla dowolnej liczby naturalnej
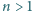 istnieją takie liczby
naturalne
istnieją takie liczby
naturalne
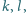 że
że
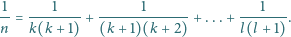
Niech
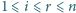 będą liczbami naturalnymi. Rozważmy
będą liczbami naturalnymi. Rozważmy
 -elementowe podzbiory zbioru
-elementowe podzbiory zbioru
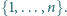 Dla takiego podzbioru
niech
Dla takiego podzbioru
niech
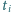 oznacza jego
oznacza jego
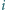 -ty element, przy założeniu, że elementy są
uporządkowane malejąco. Udowodnić, że średnia arytmetyczna wszystkich
tak uzyskanych liczb
-ty element, przy założeniu, że elementy są
uporządkowane malejąco. Udowodnić, że średnia arytmetyczna wszystkich
tak uzyskanych liczb
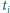 wynosi
wynosi
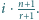
Udowodnij, że suma
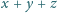 nie zależy od położenia punktu
nie zależy od położenia punktu
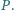
Punkt
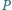 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
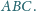 Wykaż,
że z odcinków o długościach
Wykaż,
że z odcinków o długościach
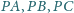 można zbudować
trójkąt.
można zbudować
trójkąt.
Wyznacz miary kątów trójkąta o bokach
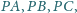 jeśli
jeśli
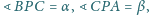
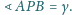
Punkt
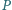 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
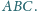 Wyznacz
pole trójkąta
Wyznacz
pole trójkąta
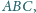 jeśli
jeśli
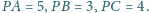
Punkt
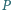 leży wewnątrz trójkąta równobocznego
leży wewnątrz trójkąta równobocznego
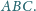 Udowodnij, że
Udowodnij, że
Czy na powierzchni każdego czworościanu można wskazać takie cztery punkty, które są wierzchołkami kwadratu, i z których żadne dwa nie leżą na jednej ścianie tego czworościanu? Odpowiedź uzasadnij.
Wyznacz wszystkie takie liczby rzeczywiste
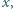 dla których liczby
dla których liczby
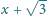 oraz
oraz
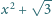 są wymierne.
są wymierne.
Sznurek godzinny to taki sznurek, który po zapaleniu spala się przez równą godzinę – ale nierównomiernie i nie wiadomo jak. Czy można ugotować jajko, które nie może gotować się krócej niż 7 minut i dłużej niż 8 minut, mając do dyspozycji trzy sznurki godzinne, kuchenkę gazową, rondelek i wodę?
Ile wynosi suma współczynników wielomianu

Miary kątów w trójkącie mają się jak
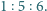 Najdłuższy bok trójkąta
to 6. Ile wynosi wysokość opuszczona na ten bok?
Najdłuższy bok trójkąta
to 6. Ile wynosi wysokość opuszczona na ten bok?
Na Wyspie Zagadkowej (jest to wyspa powstała mniej więcej 40 lat temu w Rozkoszach Łamania Głowy Lecha Pijanowskiego) mieści się ogród zoologiczny. Nie było w nim słonia. Dyrektor ZOO poprosił zatem listownie znanego łowcę zwierząt o dostarczenie słonia. Parę tygodni później łódź łowcy zwierząt ze słoniem na pokładzie przybiła do brzegu. Cena słonia, zależna od wagi, wydała się dyrektorowi mocno wygórowana. Na Wyspie Zagadkowej były jednak jedynie niewielkie wagi towarowe, nie było wagi, na której zmieściłby się słoń. Czy dyrektor mógł zważyć słonia i sprawdzić, czy łowca go nie oszukuje?
Ile, co najwyżej, ścian czworościanu może być trójkątami rozwartokątnymi?