Niby nic»Zadanie 3
Przekątne 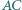 i
i 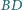 czworokąta wypukłego
czworokąta wypukłego 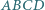 są równej długości. Punkty
są równej długości. Punkty 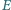 i
i 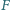 są odpowiednio środkami boków
są odpowiednio środkami boków 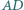 i
i 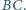 Udowodnij, że prosta
Udowodnij, że prosta 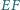 tworzy równe kąty z przekątnymi
tworzy równe kąty z przekątnymi 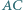 i
i 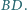
Przekątne 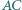 i
i 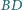 czworokąta wypukłego
czworokąta wypukłego 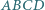 są równej długości. Punkty
są równej długości. Punkty 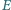 i
i 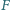 są odpowiednio środkami boków
są odpowiednio środkami boków 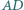 i
i 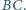 Udowodnij, że prosta
Udowodnij, że prosta 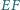 tworzy równe kąty z przekątnymi
tworzy równe kąty z przekątnymi 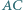 i
i 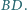
Czworokąt 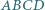 nie jest równoległobokiem oraz
nie jest równoległobokiem oraz 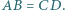 Punkty
Punkty  i
i  są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 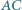 i
i 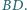 Wykaż, że rzuty prostopadłe odcinków
Wykaż, że rzuty prostopadłe odcinków 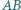 i
i 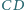 na prostą
na prostą 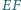 są równej długości.
są równej długości.
W sześciokącie wypukłym 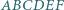 o polu 1 punkty
o polu 1 punkty 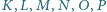 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 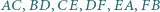 i tworzą sześciokąt wypukły
i tworzą sześciokąt wypukły 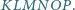 Wyznacz jego pole.
Wyznacz jego pole.
Niech 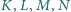 będą środkami kolejnych boków czworokąta
będą środkami kolejnych boków czworokąta 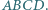 Wykaż, że
Wykaż, że 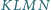 jest równoległobokiem, że
jest równoległobokiem, że 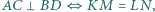 że
że 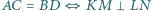 oraz wyznacz stosunek pól
oraz wyznacz stosunek pól ![N] [ABCD]. [KLM](/math/temat/matematyka/geometria/planimetria/zadania/2017/04/29/zm-17_05-deltoid-6/6x-476c50773c7ee85da9c32be7747c5f72357fd03b-im-2C,6B,73-FF,FF,FF.gif)
Dany jest trójkąt 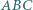 o bokach
o bokach 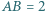 oraz
oraz 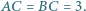 Punkt
Punkt 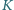 jest środkiem boku
jest środkiem boku 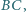 punkt
punkt 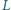 leży na boku
leży na boku 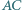 oraz
oraz 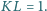 Wyznacz długość odcinka
Wyznacz długość odcinka 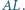
Na przyjęcie przyszło  osób w kapeluszach
osób w kapeluszach 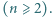 Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy
Następnie każde dwie osoby przywitały się dokładnie raz, przy czym każde powitanie polegało na zamianie kapeluszami, które w danej chwili witające się osoby miały na głowach. Okazało się, że po nastąpieniu wszystkich powitań każdy miał z powrotem swój kapelusz. Udowodnić, że taka sytuacja jest możliwa wtedy i tylko wtedy, gdy 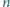 daje resztę 0 lub 1 przy dzieleniu przez 4.
daje resztę 0 lub 1 przy dzieleniu przez 4.
Niech 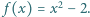 Udowodnić, że dla każdego
Udowodnić, że dla każdego 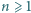 równanie
równanie
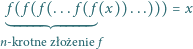
ma 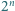 różnych rozwiązań rzeczywistych.
różnych rozwiązań rzeczywistych.
Udowodnić, że jeżeli dla pewnej liczby naturalnej 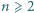 liczba
liczba 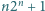 jest pierwsza, to liczby
jest pierwsza, to liczby 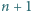 oraz
oraz 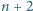 są złożone.
są złożone.
Zadanie 740 zaproponował pan Witold Bednarek z Łodzi.
Obliczyć kres dolny wartości sumy
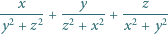
gdy  mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek
mogą być dowolnymi liczbami dodatnimi, spełniającymi warunek 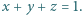
Znaleźć wszystkie funkcje 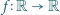 o następujących własnościach:
o następujących własnościach:
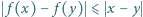 dla
dla 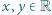 ;
;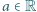 ciąg
ciąg 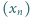 określony wzorami
określony wzorami 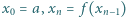 (dla
(dla 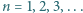 ) jest ciągiem arytmetycznym.
) jest ciągiem arytmetycznym.Czy można wyciąć w kartce dziurę w kształcie monety 1 gr, a następnie przełożyć przez tę dziurę monetę 1 zł?
Mamy kartkę o wymiarach 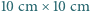 i nożyczki. Czy można wyciąć taką dziurę, przez którą przejdzie człowiek?
i nożyczki. Czy można wyciąć taką dziurę, przez którą przejdzie człowiek?
Czy w sześcianie o krawędzi 20 zmieści się kwadrat o boku 21?
Czy w sześcianie o krawędzi 20 można wywiercić tunel, przez który da się przesunąć sześcian o krawędzi 21?
Wyznacz liczbę podzbiorów zbioru 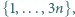 które nie zawierają dwóch liczb różniących się o
które nie zawierają dwóch liczb różniących się o 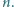
Udowodnij tożsamość 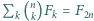 (
( 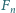 oznacza
oznacza  -tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego
-tą liczbę Fibonacciego, czyli rozwiązanie równania rekurencyjnego 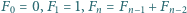 dla
dla 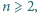 a zarazem liczbę pokryć paska
a zarazem liczbę pokryć paska 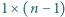 kwadratami
kwadratami 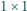 i prostokątami
i prostokątami 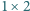 ).
).
Udowodnić, że dla każdego 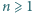 istnieje ciąg arytmetyczny
istnieje ciąg arytmetyczny  dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
dodatnich liczb całkowitych, z których każda jest podzielna przez sumę swoich cyfr (w zapisie dziesiętnym).
Wskazówka. W rozwiązaniu można skorzystać z twierdzenia o liczbach pierwszych, na przykład używając szacowania 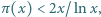 prawdziwego dla dostatecznie dużych
prawdziwego dla dostatecznie dużych 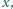 gdzie
gdzie 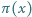 oznacza liczbę liczb pierwszych nie większych od
oznacza liczbę liczb pierwszych nie większych od 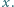
Wielokąt wypukły został podzielony odcinkami na skończoną liczbę czworokątów. Udowodnić, że co najmniej jeden z nich jest wypukły.
Na zbiorze dodatnich liczb całkowitych określone są operacje  oraz
oraz 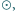 takie, że dla każdej pary
takie, że dla każdej pary 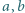 dodatnich liczb całkowitych zachodzi
dodatnich liczb całkowitych zachodzi

a ponadto  jest łączne,
jest łączne,  zaś przemienne. Czy wynika z tego, że
zaś przemienne. Czy wynika z tego, że  oraz
oraz  to "zwykłe" dodawanie i mnożenie? Czy implikacja będzie prawdziwa, jeżeli założenie o łączności operacji
to "zwykłe" dodawanie i mnożenie? Czy implikacja będzie prawdziwa, jeżeli założenie o łączności operacji  zastąpimy założeniem o jej przemienności?
zastąpimy założeniem o jej przemienności?
Zadanie 738 zaproponował pan Bartłomiej Pawlik z Limanowej.
Wypisując, jedna za drugą, wszystkie liczby całkowite dodatnie, mające (w systemie dziesiętnym) co najwyżej 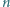 cyfr, piszemy łącznie
cyfr, piszemy łącznie 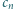 cyfr (np.
cyfr (np. 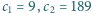 ); w tym
); w tym 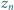 zer (np.
zer (np. 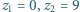 ). Czy równość
). Czy równość 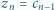 jest spełniona dla wszystkich liczb naturalnych
jest spełniona dla wszystkich liczb naturalnych 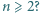
Pięciokąt 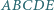 jest wpisany w okrąg
jest wpisany w okrąg 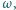 przy czym proste
przy czym proste 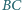 i
i 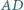 przecinają się w takim punkcie
przecinają się w takim punkcie 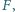 że prosta
że prosta 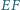 jest styczna do
jest styczna do 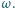 Druga prosta styczna do okręgu
Druga prosta styczna do okręgu 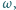 równoległa do
równoległa do 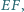 przecina proste
przecina proste 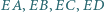 odpowiednio w punktach
odpowiednio w punktach 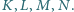 Udowodnić, że odcinki
Udowodnić, że odcinki 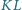 i
i 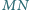 mają jednakową długość.
mają jednakową długość.
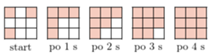
Początkowo niektóre pola tablicy 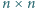 są zarażone. Infekcja rozprzestrzenia się w następujący sposób: co sekundę każde niezarażone pole, które ma wspólny bok z dokładnie dwoma zarażonymi polami, staje się zarażone. Jaka jest najmniejsza początkowa liczba zarażonych pól wystarczająca do zainfekowania po pewnym czasie całej tablicy?
są zarażone. Infekcja rozprzestrzenia się w następujący sposób: co sekundę każde niezarażone pole, które ma wspólny bok z dokładnie dwoma zarażonymi polami, staje się zarażone. Jaka jest najmniejsza początkowa liczba zarażonych pól wystarczająca do zainfekowania po pewnym czasie całej tablicy?
Przypuśćmy, że dla pewnej dodatniej liczby całkowitej 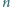 liczby
liczby 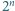 oraz
oraz 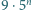 rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
rozpoczynają się w zapisie dziesiętnym tą samą cyfrą. Jaka to cyfra?
Rozważamy słowa binarne (ciągi zerojedynkowe) długości  Niech
Niech 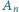 będzie liczbą takich słów, w których nie pojawia się blok
będzie liczbą takich słów, w których nie pojawia się blok 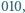 zaś
zaś 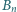 liczbą takich słów, w których w żadnym miejscu blok
liczbą takich słów, w których w żadnym miejscu blok 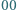 nie sąsiaduje z blokiem
nie sąsiaduje z blokiem 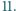 Dla każdej liczby naturalnej
Dla każdej liczby naturalnej 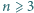 wyznaczyć wartość stosunku
wyznaczyć wartość stosunku 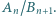
Dana jest liczba dodatnia 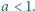 Obliczyć kres górny zbioru wartości wyrażenia
Obliczyć kres górny zbioru wartości wyrażenia 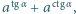 gdy zmienna
gdy zmienna 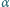 przebiega przedział
przebiega przedział 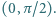
Złośliwy czarodziej rzucił urok na jedną z 1000 beczek z winem - po wypiciu choćby kropli każdy zzielenieje w ciągu doby. Codziennie rano dysponujemy 10 dzielnymi rycerzami gotowymi ponieść ryzyko. W ile dni można wykryć zaczarowaną beczkę?
Każdą liczbę całkowitą większą od 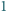 pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb
pomalowano na pewien kolor w taki sposób, że jeżeli dla pewnych dwóch liczb 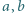 większych od
większych od 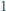 liczba
liczba 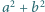 jest podzielna przez
jest podzielna przez 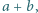 to
to 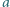 ma ten sam kolor, co
ma ten sam kolor, co 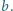 Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Jaka jest największa możliwa liczba kolorów użytych do pomalowania liczb?
Na ponad połowie pól szachownicy 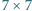 ustawiono wieże. Wykazać, że co najmniej jedna wieża jest otoczona, tzn. zarówno w wierszu, jak i w kolumnie znajduje się pomiędzy pewnymi dwiema innymi wieżami.
ustawiono wieże. Wykazać, że co najmniej jedna wieża jest otoczona, tzn. zarówno w wierszu, jak i w kolumnie znajduje się pomiędzy pewnymi dwiema innymi wieżami.