Niech 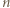 będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że
będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że 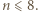 Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya:
Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya:
Twierdzenie (Ramsey). Wśród dowolnych 6 uczestników kółka można znaleźć trzech, którzy się wzajemnie lubią lub trzech, którzy się wzajemnie nie lubią.
Wybierzmy pewnego uczestnika 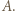 Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z
Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z 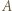 tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że
tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że 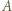 nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z
nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z 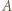 tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że
tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że 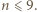 Gdyby jednak
Gdyby jednak 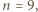 to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji
to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji 
Jeśli ponumerujemy 8 uczniów liczbami od 1 do 8 i okaże się, że uczniowie o numerach 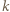 i
i 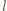 lubią się tylko wtedy, gdy
lubią się tylko wtedy, gdy 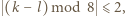 to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.
to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.

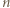 będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że
będzie liczbą uczestników pewnego kółka, spełniającego opisane w zadaniu warunki. Udowodnimy, że 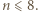 Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya:
Przydatny okaże się następujący lemat, którego dowód można znaleźć na przykład w Wikipedii pod hasłem twierdzenie Ramseya: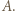 Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z
Przypuśćmy, że lubi on pewnych 6 uczestników. Zgodnie z założeniem zadania oraz powyższym lematem wśród nich znajduje się 3, którzy wzajemnie się lubią, i razem z 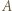 tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że
tworzą oni czwórkę, która przeczy założeniom zadania. Przypuśćmy teraz, że 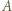 nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z
nie lubi pewnych 4 uczestników. Wśród nich znajduje się dwóch, którzy się nie lubią, i razem z 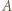 tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że
tworzą oni trójkę sprzeczną z założeniami. Wynika stąd, że 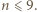 Gdyby jednak
Gdyby jednak 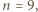 to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji
to każdy uczestnik musiałby lubić dokładnie 5 uczestników. Jest to sprzeczność, gdyż suma liczb sympatii poszczególnych uczestników wyniosłaby 45, a musi to być liczba parzysta ze względu na wzajemność uczuć. W tej sytuacji 
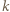 i
i 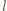 lubią się tylko wtedy, gdy
lubią się tylko wtedy, gdy 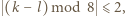 to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.
to ta grupka będzie spełniać warunki zadania, co kończy rozwiązanie.