Zagadki liczbowe»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu Zagadki liczbowe
- Publikacja w Delcie: kwiecień 2012
- Publikacja elektroniczna: 01-04-2012
Która liczba jest większa?

Która liczba jest większa?

Która liczba jest większa?
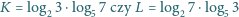
Która liczba jest większa?
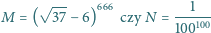
Która liczba jest większa?

Która liczba jest większa?
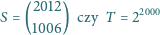
Która liczba jest większa?
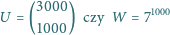
Dany jest wielomian
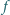 o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
o współczynnikach całkowitych, dla którego
istnieją takie parami różne liczby całkowite
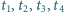 , że
, że

Udowodnić, że nie istnieje liczba całkowita
 , dla której
, dla której
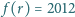 .
.
Okrąg wpisany w trójkąt
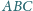 jest styczny do boków
jest styczny do boków
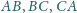 odpowiednio w punktach
odpowiednio w punktach
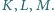 Wykaż, że
proste
Wykaż, że
proste
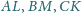 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Trapez
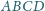 jest opisany na okręgu o środku
jest opisany na okręgu o środku
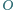 i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
i promieniu 1.
Przekątne tego trapezu przecinają się w punkcie
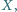 przy czym
przy czym
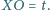 Wyznacz stosunek
Wyznacz stosunek
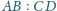 długości podstaw tego
trapezu, jeśli
długości podstaw tego
trapezu, jeśli
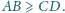
Okrąg wpisany w romb
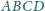 jest styczny do boku
jest styczny do boku
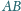 w punkcie
w punkcie
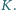 Styczna do tego okręgu przecina boki
Styczna do tego okręgu przecina boki
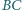 i
i
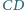 odpowiednio
w punktach
odpowiednio
w punktach
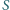 i
i
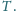 Wykaż, że
Wykaż, że

VI Olimpiada Matematyczna Gimnazjalistów (2012 r.)
Dany jest czworokąt wypukły
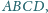 w którym zachodzi równość
w którym zachodzi równość

Punkt
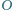 jest środkiem okręgu opisanego na trójkacie
jest środkiem okręgu opisanego na trójkacie
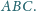 Wykaż, że punkt
Wykaż, że punkt
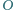 jest jednakowo odległy od prostych
jest jednakowo odległy od prostych
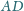 i
i
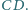
Zadanie 638 zaproponował pan Paweł Kubit z Krakowa.
Liczby dodatnie
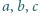 spełniają warunek
spełniają warunek
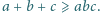 Udowodnić,
że co najwyżej jedna z liczb
Udowodnić,
że co najwyżej jedna z liczb
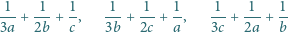
jest mniejsza od 1.
Znaleźć wszystkie liczby naturalne
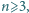 dla których zbiór
dla których zbiór
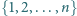 daje się przedstawić jako suma trzech rozłącznych zbiorów
o równych sumach elementów.
daje się przedstawić jako suma trzech rozłącznych zbiorów
o równych sumach elementów.
W zawodach matematycznych wzięło udział 100 uczniów. Mieli oni do rozwiązania 5 zadań. Wiadomo, że każde zadanie zostało rozwiązane przez przynajmniej 56 uczniów. Wykazać, że można wskazać takich dwóch uczniów, że każde zadanie zostało rozwiązane przynajmniej przez jednego z nich.
Mówimy, że funkcja
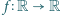 ma cykl długości
ma cykl długości
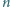 o początku
o początku
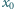 , gdy istnieje takie
, gdy istnieje takie
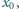 że liczby
że liczby
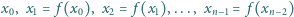 są parami różne, zaś
są parami różne, zaś
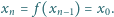
Udowodnić, że jeśli wielomian o współczynnikach całkowitych ma
cykl o początku będącym liczbą całkowitą, to jest on długości
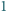 lub
lub
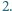
Okrąg o środku
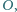 wpisany w czworokąt
wpisany w czworokąt
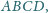 jest
styczny do boków
jest
styczny do boków
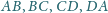 odpowiednio w punktach
odpowiednio w punktach
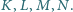 Proste
Proste
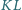 i
i
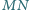 przecinają się w punkcie
przecinają się w punkcie
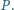 Wykaż, że proste
Wykaż, że proste
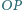 i
i
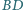 są prostopadłe.
są prostopadłe.
Dane są trzy okręgi o niewspółliniowych środkach; każda para okręgów się przecina. Wykaż, że proste zawierające ich wspólne cięciwy przecinają się w jednym punkcie.
Zadanie pochodzi z XLVI Olimpiady Matematycznej
Sześciokąt
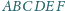 jest wypukły oraz
jest wypukły oraz
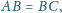
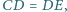
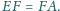 Wykaż, że proste zawierające
wysokości trójkątów
Wykaż, że proste zawierające
wysokości trójkątów
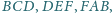 poprowadzone odpowiednio
z wierzchołków
poprowadzone odpowiednio
z wierzchołków
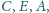 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Zadanie pochodzi z XLVI Olimpiady Matematycznej
Wewnątrz wielokąta wypukłego leży skończenie wiele parami rozłącznych okręgów. Wykaż, że można ten wielokąt podzielić na wielokąty wypukłe, z których każdy zawiera dokładnie jeden okrąg.
Różne okręgi
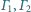 są współśrodkowe. Wykaż, że nie istnieje taki
punkt
są współśrodkowe. Wykaż, że nie istnieje taki
punkt
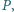 że
że
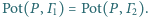
Dany jest okrąg
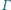 oraz punkty
oraz punkty
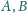 leżące w nierównych
odległościach od środka tego okręgu. Udowodnij, że wspólne cięciwy
okręgu
leżące w nierównych
odległościach od środka tego okręgu. Udowodnij, że wspólne cięciwy
okręgu
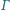 z okręgami przechodzącymi przez punkty
z okręgami przechodzącymi przez punkty
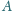 i
i
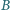 leżą na prostych mających jeden punkt wspólny.
leżą na prostych mających jeden punkt wspólny.
Dane są dwa okręgi
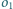 i
i
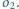 Znajdź inwersję przekształcającą
Znajdź inwersję przekształcającą
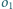 na
na
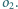
Niech
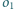 i
i
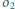 będą rozłącznymi okręgami, takimi że
będą rozłącznymi okręgami, takimi że
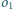 leży we wnętrzu
leży we wnętrzu
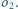 Rysujemy okrąg
Rysujemy okrąg
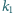 styczny
zewnętrznie do
styczny
zewnętrznie do
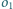 i wewnętrznie do
i wewnętrznie do
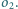 Następnie rysujemy okrąg
Następnie rysujemy okrąg
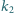 styczny zewnętrznie do
styczny zewnętrznie do
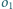 i
i
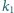 oraz wewnętrznie do
oraz wewnętrznie do
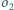 itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
itd. Jeżeli po skończonej liczbie kroków ostatni okrąg będzie styczny
zewnętrznie do
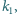 to mówimy, że okręgi
to mówimy, że okręgi
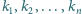 tworzą
łańcuch Steinera okręgów
tworzą
łańcuch Steinera okręgów
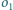 i
i
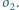 Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
Wykaż, że jeżeli istnieje
łańcuch Steinera okręgów
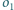 i
i
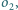 to jest to niezależne od
położenia pierwszego okręgu
to jest to niezależne od
położenia pierwszego okręgu
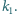
Dany jest okrąg
 i dwa rozłączne okręgi
i dwa rozłączne okręgi
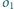 i
i
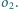 Narysuj
okrąg styczny do
Narysuj
okrąg styczny do
 i prostopadły do okręgów
i prostopadły do okręgów
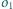 i
i
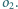
Zadanie 636 zaproponował pan Witold Bednarek z Łodzi.
Ciąg
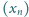 jest określony rekurencyjnie:
jest określony rekurencyjnie:
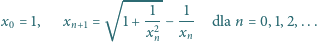
Wykazać, że ciąg
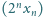 jest zbieżny i obliczyć jego granicę.
jest zbieżny i obliczyć jego granicę.