Zadanie ZM-1485
o zadaniu...
- Publikacja w Delcie: luty 2016
- Publikacja elektroniczna: 30-01-2016
Obliczyć

gdzie 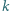 jest pewną liczbą naturalną.
jest pewną liczbą naturalną.
Obliczyć

gdzie 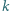 jest pewną liczbą naturalną.
jest pewną liczbą naturalną.
Znaleźć wszystkie wartości parametru 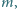 dla których wszystkie rozwiązania równania
dla których wszystkie rozwiązania równania
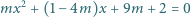
są liczbami naturalnymi.
Punkty 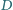 i
i 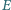 leżą odpowiednio na bokach
leżą odpowiednio na bokach 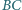 i
i 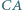 trójkąta
trójkąta 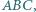 przy czym
przy czym 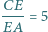 oraz
oraz 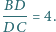 Odcinki
Odcinki 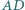 i
i 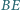 przecinają się w punkcie
przecinają się w punkcie 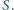 W jakim stosunku punkt
W jakim stosunku punkt 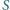 dzieli odcinek
dzieli odcinek 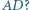
Udowodnij tożsamości

Udowodnij tożsamość

Udowodnij tożsamości

Udowodnij tożsamość
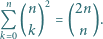
Wykaż, że
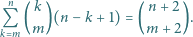
Niech 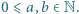 Wyznacz sumę tych
Wyznacz sumę tych 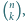 dla których
dla których 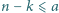 oraz
oraz 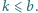
Niech

Wykaż, że 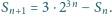
Udowodnić, że dla dowolnej liczby nieujemnej 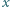 i dowolnej liczby całkowitej dodatniej
i dowolnej liczby całkowitej dodatniej 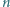 prawdziwa jest nierówność
prawdziwa jest nierówność
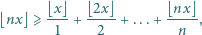
gdzie 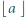 oznacza największą liczbę całkowitą nie większą od
oznacza największą liczbę całkowitą nie większą od 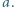
W tablicę 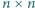 wpisano w pewnej kolejności liczby
wpisano w pewnej kolejności liczby 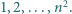 Powiemy, że para liczb sąsiaduje, jeśli znajdują się one obok siebie w pewnym wierszu lub w pewnej kolumnie. Wykazać, że istnieje para sąsiadujących liczb, które różnią się co najmniej o
Powiemy, że para liczb sąsiaduje, jeśli znajdują się one obok siebie w pewnym wierszu lub w pewnej kolumnie. Wykazać, że istnieje para sąsiadujących liczb, które różnią się co najmniej o 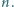
Na sferze o promieniu 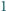 dana jest krzywa zamknięta o długości mniejszej niż
dana jest krzywa zamknięta o długości mniejszej niż 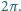 Wykazać, że ta krzywa jest zawarta w pewnej półsferze.
Wykazać, że ta krzywa jest zawarta w pewnej półsferze.
Zadanie 714 zaproponował pan Witold Bednarek z Łodzi.
Niech 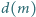 oznacza liczbę dodatnich dzielników liczby naturalnej
oznacza liczbę dodatnich dzielników liczby naturalnej 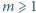
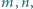 spełniających równanie
spełniających równanie 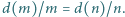
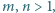 spełniających równanie
spełniających równanie 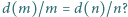
Dany jest czworokąt wypukły 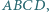 w którym boki
w którym boki 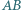 i
i 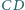 nie są równoległe. Rozważamy okrąg, przechodzący przez punkty
nie są równoległe. Rozważamy okrąg, przechodzący przez punkty 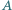 i
i 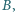 styczny do prostej
styczny do prostej 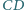 w punkcie
w punkcie 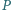 oraz okrąg, przechodzący przez punkty
oraz okrąg, przechodzący przez punkty 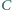 i
i 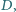 styczny do prostej
styczny do prostej 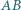 w punkcie
w punkcie 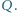 Zakładamy, że punkty
Zakładamy, że punkty 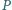 i
i 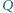 leżą na odcinkach
leżą na odcinkach 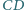 i
i 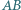 oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka
oraz że wspólna cięciwa tych okręgów przechodzi przez środek odcinka 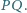 Udowodnić, że proste
Udowodnić, że proste 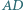 i
i 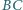 są równoległe.
są równoległe.
Udowodnij, że dla 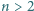 liczba
liczba 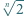 jest niewymierna.
jest niewymierna.
Wykaż, że 56 nie jest trzecią potęgą liczby naturalnej.
W dwóch urnach jest po 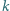 kul, każda z kul jest biała lub czarna. Z każdej z urn
kul, każda z kul jest biała lub czarna. Z każdej z urn  -krotnie losujemy kulę ze zwracaniem. Dla jakich wartości
-krotnie losujemy kulę ze zwracaniem. Dla jakich wartości 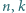 i dla jakiego układu kolorów kul prawdopodobieństwo wylosowania samych białych kul z pierwszej urny jest równe prawdopodobieństwu wylosowania z drugiej urny wszystkich kul jednego koloru?
i dla jakiego układu kolorów kul prawdopodobieństwo wylosowania samych białych kul z pierwszej urny jest równe prawdopodobieństwu wylosowania z drugiej urny wszystkich kul jednego koloru?
Znajdź wszystkie trójki dodatnich liczb całkowitych 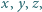 dla których
dla których 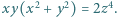
Znajdź wszystkie pary liczb całkowitych 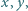 dla których
dla których 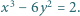
Zadanie 6 pochodzi z LXIV Olimpiady Matematycznej, a opisane tu rozwiązanie przedstawił jej uczestnik.
Czy istnieje wielomian o współczynnikach całkowitych, który nie jest różnowartościowy na zbiorze liczb rzeczywistych, ale jest różnowartościowy na zbiorze liczb wymiernych?
Niech

a 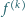 oznacza
oznacza 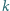 -tą pochodną
-tą pochodną 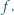 Czy
Czy 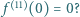
Wykazać, że w grafie prostym (tj. skończonym zbiorze wierzchołków, spośród których pewne są połączone nieskierowanymi pojedynczymi krawędziami, bez pętli) o co najmniej dwóch wierzchołkach istnieją dwa wierzchołki o tym samym stopniu.
Uwaga. Stopień wierzchołka to liczba krawędzi w nim zaczepionych.
Wykazać, że jeśli liczby całkowite dodatnie 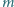 i
i  spełniają
spełniają 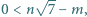 to wówczas
to wówczas 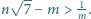
Dany jest ciąg dodatnich liczb całkowitych 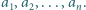 Ruch polega na wyborze dwóch takich indeksów
Ruch polega na wyborze dwóch takich indeksów 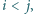 że
że 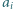 nie dzieli
nie dzieli 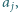 i zastąpieniu liczb
i zastąpieniu liczb 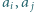 przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
przez odpowiednio ich największy wspólny dzielnik i najmniejszą wspólną wielokrotność. Udowodnić, że nie jest możliwe wykonanie nieskończenie wielu ruchów.
Udowodnić, że nie istnieje 11 liczb pierwszych mniejszych od 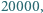 które tworzą ciąg arytmetyczny.
które tworzą ciąg arytmetyczny.
Niech 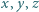 będą liczbami rzeczywistymi dodatnimi. Udowodnić, że
będą liczbami rzeczywistymi dodatnimi. Udowodnić, że

Na bokach czworokąta wypukłego 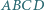 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 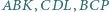 i
i 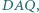 pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że
pierwsze dwa z nich na zewnątrz czworokąta, pozostałe dwa - do wewnątrz. Wykaż, że 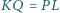 oraz
oraz 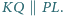
Na bokach trójkąta 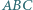 zbudowano, na zewnątrz, trójkąty równoboczne
zbudowano, na zewnątrz, trójkąty równoboczne 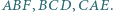 Skonstruuj trójkąt
Skonstruuj trójkąt 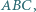 mając dane tylko punkty
mając dane tylko punkty 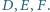
Udowodnij twierdzenie Napoleona:
Twierdzenie. Na bokach trójkąta zbudowano, na zewnątrz, trójkąty równoboczne. Wówczas ich środki tworzą trójkąt równoboczny.