Zadanie ZM-1542
o zadaniu...
- Publikacja w Delcie: wrzesień 2017
- Publikacja elektroniczna: 1 września 2017
Wykazać, że dla każdej liczby rzeczywistej 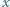 oraz dla każdej dodatniej liczby całkowitej
oraz dla każdej dodatniej liczby całkowitej 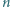 istnieje co najmniej
istnieje co najmniej 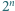 różnych wyborów znaków
różnych wyborów znaków 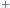 i
i  w wyrażeniu
w wyrażeniu 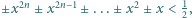 dla których ta nierówność jest spełniona.
dla których ta nierówność jest spełniona.
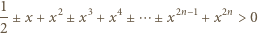
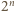 możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci
możliwych wyborów znaków. Rzeczywiście, lewą stronę powyższej nierówności można zapisać w postaci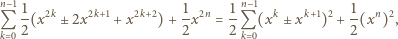
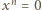 oraz
oraz 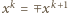 (dla
(dla 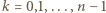 i pewnych wyborów znaków
i pewnych wyborów znaków 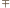 ) nie mogą wszystkie zachodzić jednocześnie.
) nie mogą wszystkie zachodzić jednocześnie.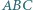 o kącie prostym przy wierzchołku
o kącie prostym przy wierzchołku 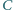 obrócono wokół prostej
obrócono wokół prostej 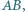 otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg
otrzymując dwa stożki obrotowe o wspólnej podstawie, której brzegiem jest okrąg  Sfera
Sfera 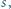 do której należy punkt
do której należy punkt 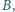 jest styczna do sfery
jest styczna do sfery 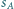 o środku
o środku 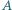 i promieniu
i promieniu 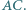 Sfery
Sfery 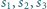 są styczne do sfery
są styczne do sfery  oraz do sfery
oraz do sfery 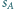 w pewnych punktach należących do okręgu
w pewnych punktach należących do okręgu 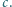 Udowodnić, że sfery
Udowodnić, że sfery 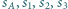 mają wspólną płaszczyznę styczną.
mają wspólną płaszczyznę styczną.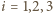 oznaczmy przez
oznaczmy przez 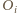 środek sfery
środek sfery 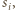 a przez
a przez 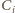 - punkt styczności sfery
- punkt styczności sfery 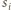 ze sferą
ze sferą 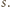 Ponieważ
Ponieważ 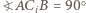 oraz punkty
oraz punkty 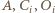 są współliniowe, więc również
są współliniowe, więc również 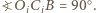
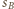 o środku
o środku 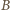 i promieniu
i promieniu 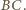 Dla
Dla 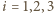 sfera
sfera 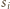 jest prostopadła do sfery
jest prostopadła do sfery 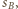 więc jest zachowywana przy rozważanej inwersji. Tę samą własność ma sfera
więc jest zachowywana przy rozważanej inwersji. Tę samą własność ma sfera 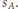 Wobec tego obrazem sfery
Wobec tego obrazem sfery  (przechodzącej przez środek inwersji) jest pewna płaszczyzna, która jest styczna do
(przechodzącej przez środek inwersji) jest pewna płaszczyzna, która jest styczna do 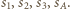
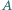 i
i 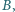 że
że
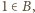 to dla dowolnego
to dla dowolnego 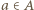 mamy
mamy 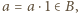 co jest sprzeczne z założeniem, że zbiory
co jest sprzeczne z założeniem, że zbiory 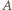 i
i 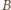 są rozłączne. Wobec tego
są rozłączne. Wobec tego 
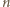 najmniejszy element zbioru
najmniejszy element zbioru 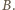 Korzystając z pierwszego z danych warunków, łatwo indukcyjnie udowodnić, że dla każdej dodatniej liczby całkowitej
Korzystając z pierwszego z danych warunków, łatwo indukcyjnie udowodnić, że dla każdej dodatniej liczby całkowitej 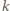 :
: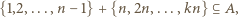
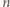 należą do zbioru
należą do zbioru 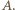 W szczególności z drugiego z danych warunków wynika, że każda liczba podzielna przez
W szczególności z drugiego z danych warunków wynika, że każda liczba podzielna przez 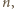 ale niepodzielna przez
ale niepodzielna przez 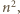 należy do zbioru
należy do zbioru 
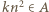 dla pewnej dodatniej liczby całkowitej
dla pewnej dodatniej liczby całkowitej 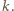 Wówczas, skoro
Wówczas, skoro 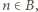 to
to 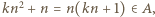 co jest sprzeczne z konkluzją poprzedniego akapitu. To oznacza, że wszystkie liczby podzielne przez
co jest sprzeczne z konkluzją poprzedniego akapitu. To oznacza, że wszystkie liczby podzielne przez 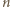 należą do zbioru
należą do zbioru 
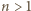 jeżeli
jeżeli 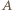 jest zbiorem liczb niepodzielnych przez
jest zbiorem liczb niepodzielnych przez 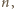 a
a 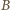 - zbiorem liczb podzielnych przez
- zbiorem liczb podzielnych przez 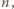 to warunki zadania są spełnione.
to warunki zadania są spełnione.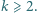 Czy istnieje rosnący ciąg liczb naturalnych
Czy istnieje rosnący ciąg liczb naturalnych 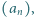 którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest
którego żaden wyraz ani żadna suma skończenie wielu jego wyrazów nie jest 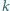 -tą potęgą liczby naturalnej, a przy tym ciąg
-tą potęgą liczby naturalnej, a przy tym ciąg 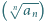 jest ograniczony?
jest ograniczony?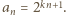
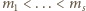 :
: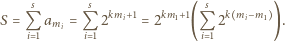
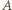 zachodziła równość
zachodziła równość 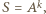 wówczas pisząc
wówczas pisząc 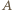 w postaci
w postaci 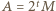 (
( 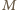 nieparzyste) i przyrównując potęgi dwójki w
nieparzyste) i przyrównując potęgi dwójki w 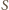 i w
i w 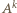 uzyskalibyśmy równość
uzyskalibyśmy równość 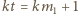 ; oczywista sprzeczność.
; oczywista sprzeczność.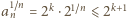 jest ograniczony.
jest ograniczony.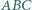 leżą cztery różne punkty
leżą cztery różne punkty 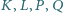 : punkty
: punkty 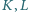 na boku
na boku 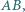 punkty
punkty 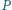 i
i 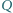 odpowiednio na bokach
odpowiednio na bokach 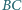 i
i 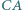 ; przy tym odcinki
; przy tym odcinki 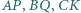 i
i 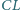 mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.
mają jednakową długość. Udowodnić, że środki tych czterech odcinków leżą na jednym okręgu.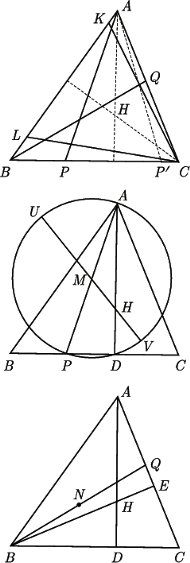
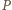 przez
przez 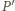 - drugi punkt prostej
- drugi punkt prostej 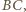 leżący w tej samej odległości od
leżący w tej samej odległości od 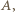 co punkt
co punkt 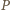 ; zaś środek szukanego okręgu powinien leżeć na osiach symetrii trójkątów równoramiennych
; zaś środek szukanego okręgu powinien leżeć na osiach symetrii trójkątów równoramiennych 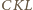 i
i 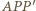 - czyli na wysokościach trójkąta
- czyli na wysokościach trójkąta 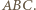 Stąd domysł uściślenia tezy zadania: wykazać, że środki odcinków
Stąd domysł uściślenia tezy zadania: wykazać, że środki odcinków 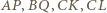 (o jednakowej długości
(o jednakowej długości 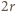 ) leżą na okręgu o środku
) leżą na okręgu o środku 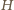 (ortocentrum trójkąta
(ortocentrum trójkąta 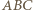 ).
).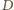 będzie spodkiem wysokości opuszczonej z wierzchołka
będzie spodkiem wysokości opuszczonej z wierzchołka 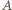 i niech
i niech 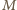 będzie środkiem odcinka
będzie środkiem odcinka 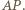 Weźmy pod uwagę okrąg o środku
Weźmy pod uwagę okrąg o środku 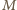 i promieniu
i promieniu  (czyli o średnicy
(czyli o średnicy 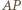 ). Prosta
). Prosta 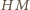 przecina ów okrąg w punktach
przecina ów okrąg w punktach 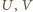 (gdy punkty
(gdy punkty 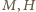 pokrywają się, przyjmijmy
pokrywają się, przyjmijmy 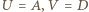 ). Cięciwa
). Cięciwa 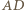 tego okręgu oraz jego średnica
tego okręgu oraz jego średnica 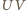 przecinają się w punkcie
przecinają się w punkcie  Zatem
Zatem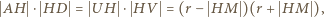
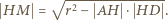
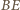 jest drugą wysokością trójkąta
jest drugą wysokością trójkąta 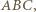 a
a 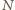 jest środkiem odcinka
jest środkiem odcinka 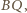 to analogicznie uzyskujemy równość
to analogicznie uzyskujemy równość
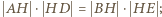 wynika to z podobieństwa trójkątów
wynika to z podobieństwa trójkątów 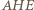 i
i 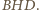 Tak więc
Tak więc 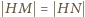 ; środki odcinków
; środki odcinków 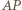 i
i 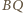 leżą w jednakowej odległości od punktu
leżą w jednakowej odległości od punktu 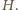 Analogicznie, w tej samej odległości od
Analogicznie, w tej samej odległości od 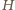 leżą też środki odcinków
leżą też środki odcinków 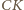 i
i 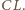 To właśnie nasza teza.
To właśnie nasza teza.
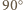 ).
).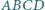 krawędź
krawędź 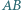 jest prostopadła do krawędzi
jest prostopadła do krawędzi 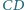 i
i 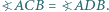 Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź
Rozstrzygnij, czy oznacza to, że płaszczyzna wyznaczona przez krawędź 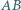 i środek krawędzi
i środek krawędzi 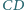 jest prostopadła do krawędzi
jest prostopadła do krawędzi 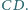
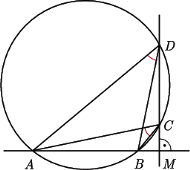
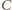 i
i 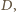 a więc też trójkąty
a więc też trójkąty 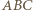 i
i 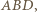 są symetryczne względem opisanej płaszczyzny, zatem przystające. Wykażemy, że tak być nie musi.
są symetryczne względem opisanej płaszczyzny, zatem przystające. Wykażemy, że tak być nie musi.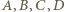 leżą na jednym okręgu w tej właśnie kolejności, przy czym
leżą na jednym okręgu w tej właśnie kolejności, przy czym 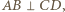 a
a 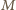 to punkt przecięcia tych prostych. Wówczas trójkąty
to punkt przecięcia tych prostych. Wówczas trójkąty 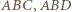 nie są przystające (mają różne wysokości na
nie są przystające (mają różne wysokości na 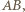 więc też różne pola). Jednocześnie
więc też różne pola). Jednocześnie 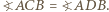
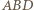 wokół prostej
wokół prostej 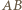 o pewien dodatni kąt mniejszy od
o pewien dodatni kąt mniejszy od 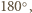 otrzymamy czworościan
otrzymamy czworościan 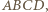 w którym
w którym 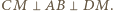 Wobec tego prosta
Wobec tego prosta 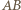 jest prostopadła do płaszczyzny
jest prostopadła do płaszczyzny 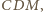 a więc także do każdej prostej zawartej w tej płaszczyźnie. Stąd
a więc także do każdej prostej zawartej w tej płaszczyźnie. Stąd 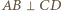 także po opisanym obrocie. Uzyskaliśmy więc czworościan
także po opisanym obrocie. Uzyskaliśmy więc czworościan 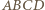 spełniający warunki zadania, w którym trójkąty
spełniający warunki zadania, w którym trójkąty 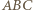 i
i 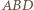 nie są przystające.
nie są przystające.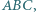 mając dane punkty
mając dane punkty 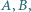 kąt przy wierzchołku
kąt przy wierzchołku 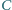 oraz długość środkowej
oraz długość środkowej 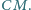 Ile rozwiązań może mieć to zadanie?
Ile rozwiązań może mieć to zadanie?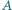 i
i 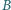 należą do wnętrza kąta ostrego
należą do wnętrza kąta ostrego 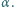 Skonstruuj taki trójkąt równoramienny, aby punkty
Skonstruuj taki trójkąt równoramienny, aby punkty 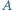 i
i 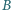 należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta
należały do różnych jego ramion, aby podstawa tego trójkąta była zawarta w jednym z ramion kąta 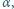 a wierzchołek należał do drugiego z ramion.
a wierzchołek należał do drugiego z ramion.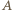 symetrycznie w jednym z ramion kąta, otrzymując
symetrycznie w jednym z ramion kąta, otrzymując 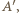 narysuj łuk Talesa dla odcinka
narysuj łuk Talesa dla odcinka 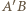 i kąta
i kąta 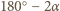 i rozważ odpowiedni jego punkt przecięcia z wybranym wcześniej ramieniem kąta.
i rozważ odpowiedni jego punkt przecięcia z wybranym wcześniej ramieniem kąta.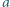 i
i 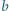 jest równy
jest równy 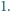 Dowieść, że największy wspólny dzielnik liczb
Dowieść, że największy wspólny dzielnik liczb 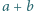 i
i 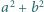 nie przekracza
nie przekracza 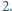
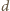 największy wspólny dzielnik liczb
największy wspólny dzielnik liczb 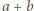 i
i 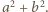 Ponieważ liczby
Ponieważ liczby 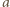 i
i 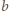 są względnie pierwsze, a ich suma jest podzielna przez
są względnie pierwsze, a ich suma jest podzielna przez 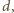 więc liczba
więc liczba 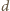 jest względnie pierwsza z liczbami
jest względnie pierwsza z liczbami 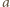 i
i 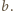 Ponadto liczba
Ponadto liczba 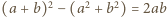 jest podzielna przez
jest podzielna przez 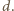 Stąd wynika, że
Stąd wynika, że 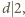 czyli
czyli 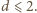
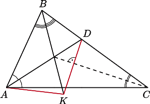
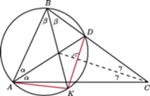
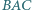 trójkąta
trójkąta 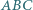 przecina bok
przecina bok 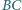 w punkcie
w punkcie 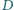 (rys.). Prosta przechodząca przez punkt
(rys.). Prosta przechodząca przez punkt 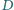 i prostopadła do dwusiecznej kąta
i prostopadła do dwusiecznej kąta 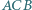 przecina dwusieczną kąta
przecina dwusieczną kąta 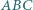 w punkcie
w punkcie 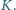 Udowodnić, że
Udowodnić, że 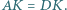
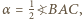
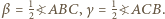 Wówczas
Wówczas 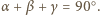 Mamy
Mamy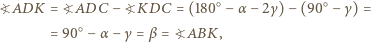
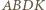 można opisać okrąg. Z rowności
można opisać okrąg. Z rowności 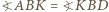 wynika zatem, że
wynika zatem, że 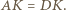
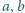 spełniają warunek
spełniają warunek 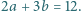 Wykazać, że dla każdej liczby naturalnej
Wykazać, że dla każdej liczby naturalnej 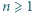 zachodzi nierówność
zachodzi nierówność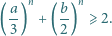
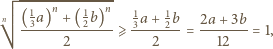
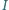 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 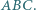 Prosta
Prosta 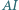 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 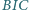 w punktach
w punktach 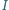 i
i 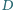 ; prosta
; prosta 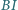 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 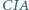 w punktach
w punktach 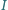 i
i 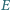 ; prosta
; prosta 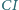 przecina okrąg opisany na trójkącie
przecina okrąg opisany na trójkącie 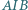 w punktach
w punktach 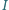 i
i 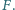 Wyznaczyć największą możliwą wartość iloczynu
Wyznaczyć największą możliwą wartość iloczynu 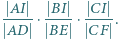
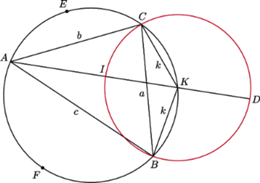
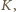 w którym prosta
w którym prosta 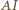 przecina ponownie okrąg opisany na trójkącie
przecina ponownie okrąg opisany na trójkącie 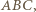 jest środkiem łuku
jest środkiem łuku 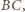 więc cięciwy
więc cięciwy 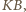
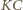 mają równą długość
mają równą długość 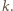 Tę samą długość ma też odcinek
Tę samą długość ma też odcinek 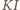 (fakt znany lub łatwy do udowodnienia). Zatem okrąg opisany na trójkącie
(fakt znany lub łatwy do udowodnienia). Zatem okrąg opisany na trójkącie 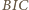 ma środek w punkcie
ma środek w punkcie 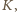 a odcinek
a odcinek 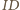 jest jego średnicą.
jest jego średnicą.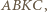 daje równość
daje równość 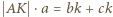 (gdzie jak zwykle
(gdzie jak zwykle 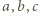 to długości boków trójkąta
to długości boków trójkąta 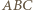 ). Stąd
). Stąd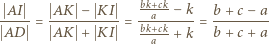
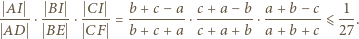
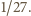
 dla pewnych liczb naturalnych
dla pewnych liczb naturalnych 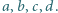
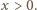
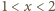 ; tak więc
; tak więc 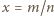
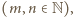
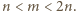 W tym przypadku wystarczy przyjąć
W tym przypadku wystarczy przyjąć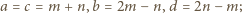
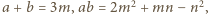
![a3 + b3 = (a +b)[(a + b)2− 3ab] = 3m(3m2](/math/temat/matematyka/algebra/zadania/2017/08/22/zm-k44-495/7x-65a3a08157267fadfd427493aa9c892345a613f2-dm-66,57,43-FF,FF,FF.gif)
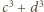 i otrzymujemy
i otrzymujemy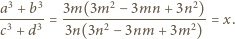
 jest dowolną liczbą wymierną dodatnią, znajdujemy liczbę wymierną
jest dowolną liczbą wymierną dodatnią, znajdujemy liczbę wymierną 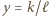 taką, że
taką, że 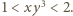 W myśl konkluzji poprzedniego przypadku liczba
W myśl konkluzji poprzedniego przypadku liczba 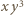 daje się zapisać jako ułamek
daje się zapisać jako ułamek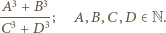
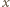 :
: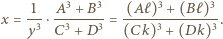
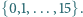 Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.
Mamy prawo zadać 7 pytań, oczekując odpowiedzi Tak lub Nie. Przeciwnik na wszystkie pytania odpowiada; wolno mu przy tym skłamać, ale co najwyżej jeden raz. Podać taktykę gwarantującą prawidłowe rozpoznanie wybranej liczby.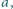 dla której zachodzi implikacja:
dla której zachodzi implikacja: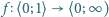 spełnia warunki
spełnia warunki 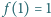 oraz
oraz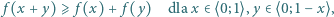
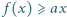 dla
dla 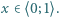
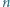 będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać
będzie liczbą naturalną większą od 4. Udowodnić, że w elipsę o półosiach różnej długości nie można wpisać 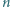 -kąta foremnego.
-kąta foremnego.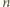 -kącie foremnym przecinałby elipsę przynajmniej w pięciu punktach, a to nie jest możliwe.
-kącie foremnym przecinałby elipsę przynajmniej w pięciu punktach, a to nie jest możliwe.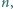 dla której
dla której 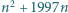 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.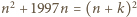 dla pewnego naturalnego
dla pewnego naturalnego 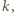 to
to 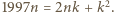 Stąd
Stąd 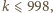 a wtedy
a wtedy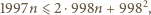
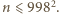 Z drugiej strony
Z drugiej strony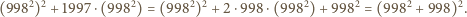
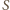 oznacza pole trójkąta,
oznacza pole trójkąta, 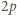 - jego obwód,
- jego obwód,  - promień okręgu wpisanego, zaś
- promień okręgu wpisanego, zaś 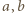 i
i  - długości boków, to wówczas
- długości boków, to wówczas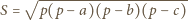
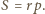 Z tych wzorów wynika, że
Z tych wzorów wynika, że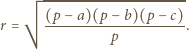
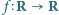 spełnia wraz z pewną funkcją
spełnia wraz z pewną funkcją 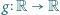 równanie
równanie 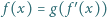 dla
dla 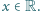 Dowieść, że funkcja
Dowieść, że funkcja 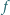 jest wypukła lub wklęsła.
jest wypukła lub wklęsła.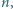 dla której istnieją czteroelementowe zbiory
dla której istnieją czteroelementowe zbiory 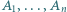 o następującej własności: każdy zbiór
o następującej własności: każdy zbiór 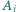 ma z każdym innym zbiorem
ma z każdym innym zbiorem 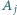 dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów
dokładnie jeden element wspólny, ale nie istnieje wspólny element wszystkich zbiorów 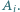
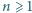 oraz pewien zbiór
oraz pewien zbiór 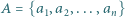 dodatnich liczb całkowitych. Na okręgu wyróżniono
dodatnich liczb całkowitych. Na okręgu wyróżniono 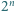 punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru
punktów i każdemu z nich przyporządkowano jedną z liczb ze zbioru 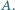 Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.
Udowodnić, że iloczyn liczb znajdujących się na pewnym łuku tego okręgu jest kwadratem liczby całkowitej.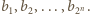 Dla każdej liczby
Dla każdej liczby 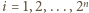 zdefiniujmy
zdefiniujmy 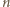 -wyrazowy ciąg binarny
-wyrazowy ciąg binarny 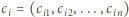 następująco:
następująco: 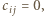 jeżeli pośród liczb
jeżeli pośród liczb 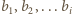 wartość
wartość 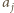 występuje parzystą liczbę razy oraz
występuje parzystą liczbę razy oraz 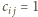 w przeciwnym przypadku.
w przeciwnym przypadku.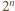 binarnych ciągów długości
binarnych ciągów długości 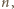 więc albo ciągi
więc albo ciągi 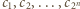 są parami różne i
są parami różne i 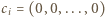 dla pewnego
dla pewnego 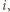 albo
albo 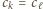 dla pewnych
dla pewnych 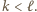 W pierwszym przypadku iloczyn liczb
W pierwszym przypadku iloczyn liczb 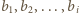 jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb
jest kwadratem liczby całkowitej, w drugim zaś - iloczyn liczb 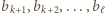 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej.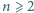 będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby
będzie liczbą całkowitą. Znaleźć liczbę przedstawień liczby 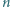 w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.
w postaci sumy pewnej liczby dodatnich całkowitych składników, pośród których jest parzysta liczba liczb parzystych.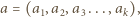
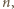 nazwiemy kompozycją liczby
nazwiemy kompozycją liczby 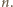
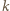 -elementowe kompozycje liczby
-elementowe kompozycje liczby 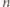 pozostają we wzajemnie jednoznacznej odpowiedniości z
pozostają we wzajemnie jednoznacznej odpowiedniości z 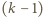 -elementowymi podzbiorami zbioru
-elementowymi podzbiorami zbioru 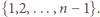 Każdej takiej kompozycji
Każdej takiej kompozycji 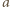 możemy przypisać zbiór
możemy przypisać zbiór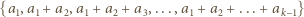
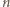 jest równa liczbie podzbiorów zbioru
jest równa liczbie podzbiorów zbioru 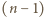 -elementowego, czyli
-elementowego, czyli 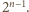
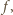 która przyporządkowuje każdej kompozycji
która przyporządkowuje każdej kompozycji  liczby
liczby 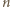 pewną kompozycję następująco: jeżeli
pewną kompozycję następująco: jeżeli 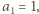 to
to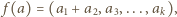
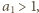 to
to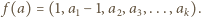
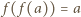 dla każdej kompozycji
dla każdej kompozycji 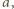 więc
więc 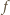 zadaje podział zbioru wszystkich kompozycji liczby
zadaje podział zbioru wszystkich kompozycji liczby 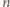 na pary. Wprost z definicji
na pary. Wprost z definicji 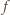 wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli
wynika, że kompozycje w obrębie każdej pary różnią się parzystością liczby parzystych wyrazów. To oznacza, że liczba kompozycji zawierających parzystą liczbę liczb parzystych jest równa połowie liczby wszystkich kompozycji, czyli 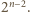
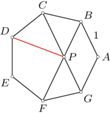
 o boku długości
o boku długości 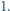 Przekątne
Przekątne 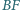 i
i 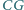 przecinają się w punkcie
przecinają się w punkcie 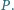 Znaleźć długość odcinka
Znaleźć długość odcinka 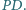
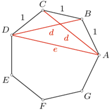
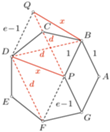
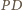 przez
przez 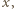 a krótszej i dłuższej przekątnej danego siedmiokąta foremnego odpowiednio przez
a krótszej i dłuższej przekątnej danego siedmiokąta foremnego odpowiednio przez 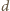 i
i 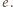 Wówczas na mocy twierdzenia Ptolemeusza, zastosowanego do trapezu równoramiennego
Wówczas na mocy twierdzenia Ptolemeusza, zastosowanego do trapezu równoramiennego 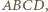 uzyskujemy
uzyskujemy 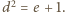
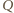 będzie takim punktem, że czworokąt
będzie takim punktem, że czworokąt 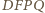 jest równoległobokiem. Wówczas
jest równoległobokiem. Wówczas 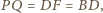 więc trapez
więc trapez 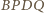 jest równoramienny. Stosując do niego twierdzenie Ptolemeusza, otrzymujemy
jest równoramienny. Stosując do niego twierdzenie Ptolemeusza, otrzymujemy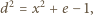
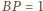 oraz
oraz 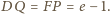 Łącząc uzyskane równości, mamy
Łącząc uzyskane równości, mamy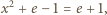
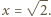
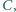 są styczne do prostej
są styczne do prostej 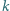 w punktach
w punktach 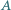 i
i 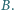 Wykaż, że trójkąt
Wykaż, że trójkąt 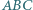 jest prostokątny.
jest prostokątny.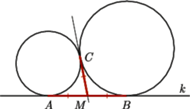
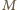 będzie punktem przecięcia prostej
będzie punktem przecięcia prostej 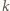 z prostą styczną do obu okręgów, przechodzącą przez
z prostą styczną do obu okręgów, przechodzącą przez 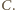 Wówczas
Wówczas 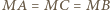 jako odcinki stycznych. Teza wynika z faktu
jako odcinki stycznych. Teza wynika z faktu 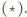
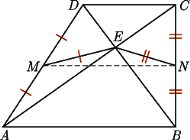
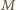 i
i 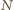 środki ramion
środki ramion 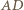 i
i 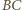 trapezu, a przez
trapezu, a przez 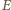 punkt przecięcia jego przekątnych. Wówczas na mocy nierówności trójkąta
punkt przecięcia jego przekątnych. Wówczas na mocy nierówności trójkąta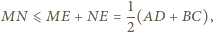
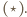 Jednocześnie w trapezie
Jednocześnie w trapezie 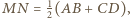 co kończy dowód.
co kończy dowód.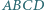 wybrano taki punkt
wybrano taki punkt 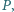 że
że 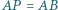 oraz
oraz 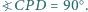 Wykaż, że
Wykaż, że 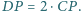
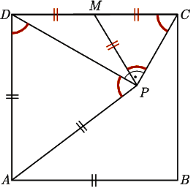
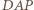 jest równoramienny, gdyż
jest równoramienny, gdyż 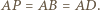 Ponadto
Ponadto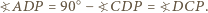
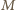 będzie środkiem boku
będzie środkiem boku 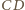 trójkąta prostokątnego
trójkąta prostokątnego 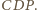 Wówczas trójkąt
Wówczas trójkąt 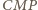 jest równoramienny i na mocy powyższej równości kątów podobny do trójkąta
jest równoramienny i na mocy powyższej równości kątów podobny do trójkąta 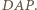 Stąd
Stąd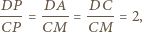
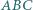 środkowe poprowadzone z wierzchołków
środkowe poprowadzone z wierzchołków 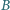 i
i 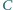 są prostopadłe oraz
są prostopadłe oraz 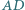 jest wysokością. Wykaż, że
jest wysokością. Wykaż, że 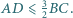
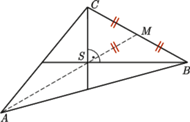
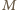 będzie środkiem boku
będzie środkiem boku 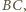 a
a 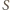 - środkiem ciężkości trójkąta
- środkiem ciężkości trójkąta  Wówczas
Wówczas