Zadania z matematyki - VIII 2020»Zadanie 1647
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - VIII 2020
- Publikacja w Delcie: sierpień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Niech 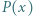 będzie wielomianem
będzie wielomianem 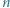 -tego stopnia
-tego stopnia 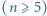 o współczynnikach całkowitych, mającym
o współczynnikach całkowitych, mającym 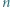 różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian
różnych pierwiastków całkowitych. Załóżmy, że 0 jest jednym z jego pierwiastków. Udowodnić, że wielomian 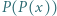 również ma dokładnie
również ma dokładnie  różnych pierwiastków całkowitych.
różnych pierwiastków całkowitych.

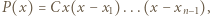 gdzie
gdzie 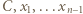 są liczbami całkowitymi. Oczywiście
są liczbami całkowitymi. Oczywiście 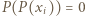 dla
dla 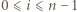 (przyjmujemy
(przyjmujemy 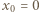 ). Załóżmy, że
). Załóżmy, że 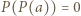 dla pewnego
dla pewnego 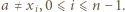 Wówczas
Wówczas 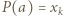 dla pewnego
dla pewnego 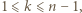 czyli
czyli 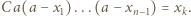 W tej sytuacji
W tej sytuacji 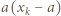 dzieli
dzieli 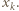 Załóżmy, że
Załóżmy, że 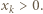 Z podzielności
Z podzielności 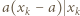 wnioskujemy kolejno
wnioskujemy kolejno 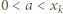 oraz
oraz 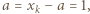 czyli
czyli 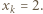 Jednak
Jednak 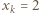 ma tylko 4 różne dzielniki całkowite, co przeczy równości
ma tylko 4 różne dzielniki całkowite, co przeczy równości 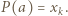 Przypadek
Przypadek 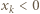 rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu
rozpatrujemy podobnie i w ten sposób kończymy dowód, że tylko pierwiastki wielomianu 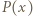 są całkowitymi pierwiastkami wielomianu
są całkowitymi pierwiastkami wielomianu 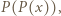 co dopełnia rozwiązanie.
co dopełnia rozwiązanie.