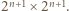W poszukiwaniu trójkąta równobocznego»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu W poszukiwaniu trójkąta równobocznego
- Publikacja w Delcie: wrzesień 2019
- Publikacja elektroniczna: 1 września 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (350 KB)
Na bokach trójkąta 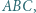 na zewnątrz niego, zbudowano trójkąty równoboczne
na zewnątrz niego, zbudowano trójkąty równoboczne 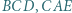 i
i 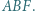 Środkami tych trójkątów są odpowiednio punkty
Środkami tych trójkątów są odpowiednio punkty 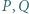 i
i 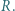 Dowieść, że trójkąt
Dowieść, że trójkąt 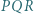 jest równoboczny (twierdzenie Napoleona).
jest równoboczny (twierdzenie Napoleona).
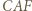 jest podobny do trójkąta
jest podobny do trójkąta 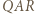 w skali
w skali 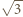 (bkb), analogicznie trójkąt
(bkb), analogicznie trójkąt 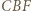 do
do 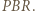 Stąd
Stąd 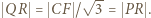 Tą samą metodą dowodzimy, że
Tą samą metodą dowodzimy, że 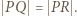
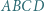 o podstawach
o podstawach 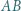 i
i 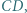 w którym
w którym 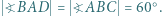 Na boku
Na boku 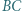 tego trapezu leży taki punkt
tego trapezu leży taki punkt 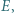 że
że 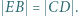 Wykazać, że
Wykazać, że 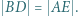
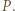 Wówczas trójkąty
Wówczas trójkąty 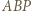 i
i 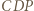 są równoboczne, dalej dowodzimy, że trójkąty
są równoboczne, dalej dowodzimy, że trójkąty 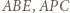 i
i 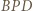 są przystające (bkb).
są przystające (bkb).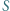 leży wewnątrz sześciokąta foremnego
leży wewnątrz sześciokąta foremnego 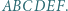 Udowodnić, że suma pól trójkątów
Udowodnić, że suma pól trójkątów 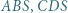 i
i 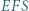 jest równa sumie pól trójkątów
jest równa sumie pól trójkątów 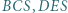 i
i 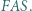
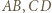 i
i 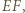 otrzymując trójkąt równoboczny. Suma pól trójkątów
otrzymując trójkąt równoboczny. Suma pól trójkątów 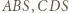 i
i 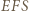 stanowi
stanowi 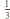 pola tego trójkąta.
pola tego trójkąta.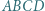 mamy
mamy 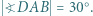 Wykazać, że
Wykazać, że 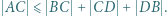
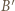 będzie punktem symetrycznym do
będzie punktem symetrycznym do 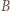 względem prostej
względem prostej 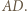 Wówczas trójkąt
Wówczas trójkąt 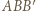 jest równoboczny oraz
jest równoboczny oraz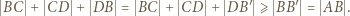
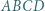 wszystkie kąty płaskie przy wierzchołku
wszystkie kąty płaskie przy wierzchołku 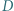 mają miarę
mają miarę 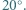 Wykazać, że
Wykazać, że 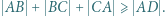
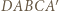 będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi
będzie siatką tego czworościanu po rozcięciu wzdłuż krawędzi 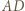 i usunięciu ściany
i usunięciu ściany 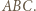 Wówczas trójkąt
Wówczas trójkąt 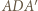 jest równoboczny.
jest równoboczny.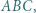 w którym
w którym 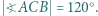 Punkt
Punkt 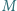 jest środkiem boku
jest środkiem boku 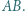 Na odcinkach
Na odcinkach 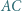 i
i 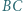 wybrano odpowiednio takie punkty
wybrano odpowiednio takie punkty 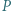 i
i 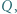 że
że 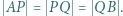 Wykazać, że
Wykazać, że 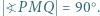
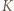 będzie symetryczny do
będzie symetryczny do 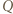 względem
względem 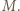 Wówczas trójkąt
Wówczas trójkąt 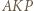 jest równoboczny.
jest równoboczny.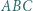 mamy
mamy 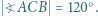 Punkty
Punkty 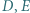 i
i 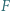 leżą na bokach odpowiednio
leżą na bokach odpowiednio 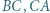 i
i 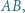 przy czym proste
przy czym proste 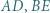 i
i 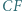 są dwusiecznymi kątów trójkąta
są dwusiecznymi kątów trójkąta 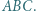 Udowodnić, że
Udowodnić, że 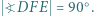
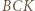 na zewnątrz trójkąta
na zewnątrz trójkąta 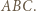 Wtedy
Wtedy 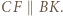 Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów
Korzystając z twierdzenia o dwusiecznej oraz podobieństwa trójkątów 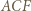 i
i 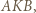 wykażemy, że
wykażemy, że 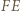 jest dwusieczną kąta
jest dwusieczną kąta 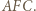 Analogicznie
Analogicznie 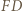 jest dwusieczną kąta
jest dwusieczną kąta 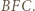
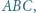 w którym
w którym 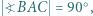 jest podstawą ostrosłupa
jest podstawą ostrosłupa 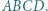 Ponadto zachodzą równości
Ponadto zachodzą równości 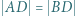 oraz
oraz 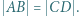 Udowodnić, że
Udowodnić, że 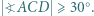
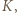 by czworokąt
by czworokąt 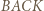 był prostokątem. Wtedy trójkąt
był prostokątem. Wtedy trójkąt 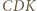 jest równoboczny. Z nierówności kąta trójściennego mamy
jest równoboczny. Z nierówności kąta trójściennego mamy 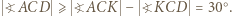
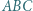 wybrano taki punkt
wybrano taki punkt 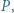 dla którego wartość wyrażenia
dla którego wartość wyrażenia 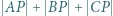 jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że
jest najmniejsza (punkt Fermata-Torricellego). Wykazać, że 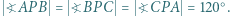
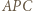 o
o 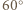 wokół punktu
wokół punktu 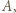 w kierunku zgodnym z orientacją trójkąta
w kierunku zgodnym z orientacją trójkąta 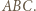 Otrzymamy trójkąt
Otrzymamy trójkąt 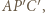 przystający do
przystający do 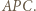 Trójkąt
Trójkąt 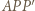 jest równoboczny, więc
jest równoboczny, więc 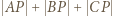 jest równe długości łamanej
jest równe długości łamanej 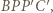 która jest najkrótsza, gdy jej wierzchołki są współliniowe.
która jest najkrótsza, gdy jej wierzchołki są współliniowe.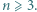 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 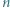 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 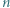 -kąta. Wykazać, że
-kąta. Wykazać, że 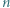 jest liczbą nieparzystą.
jest liczbą nieparzystą.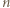 -kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.
-kąta czadowym i zauważmy, że liczba czadowych trójkątów jest równa liczbie trójek kolorów. To oznacza, że jeśli warunki zadania są spełnione, to każda trójka kolorów pojawia się jako zbiór kolorów boków czadowego trójkąta dokładnie raz. W szczególności żaden czadowy trójkąt nie może mieć dwóch boków tego samego koloru.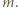 Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa
Z jednej strony liczba czadowych trójkątów o czerwonym boku jest równa 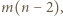 gdyż każdy czerwony odcinek jest bokiem dokładnie
gdyż każdy czerwony odcinek jest bokiem dokładnie 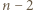 czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród
czadowych trójkątów. Z drugiej strony liczba ta jest równa liczbie sposobów doboru dwóch innych spośród  dostępnych kolorów do czerwonego, czyli
dostępnych kolorów do czerwonego, czyli 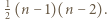 Stąd
Stąd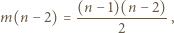
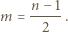
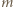 jest liczbą całkowitą, to
jest liczbą całkowitą, to 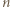 jest liczbą nieparzystą.
jest liczbą nieparzystą.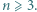 Każdy bok i każdą przekątną
Każdy bok i każdą przekątną 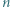 -kąta foremnego pomalowano przy użyciu jednego z
-kąta foremnego pomalowano przy użyciu jednego z  kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego
kolorów w taki sposób, że dwa odcinki mają ten sam kolor dokładnie wtedy, gdy są równoległe. Wykazać, że dla każdej trójki kolorów istnieje trójkąt o bokach w tych właśnie kolorach wyznaczony przez trzy spośród wierzchołków danego 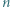 -kąta.
-kąta.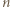 -kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.
-kąta czadowym. Zauważmy, że skoro każde dwa jednokolorowe odcinki są równoległe, to każdy czadowy trójkąt ma różnokolorowe boki. Liczba trójek kolorów jest równa liczbie czadowych trójkątów, więc do rozwiązania zadania wystarczy wykazać, że każde dwa różne czadowe trójkąty mają różne zbiory kolorów boków.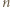 -kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego
-kącie foremnym), to są przystające, a rozważana jednokładność jest symetrią względem środka tego okręgu. To jednak oznacza, że pewne dwa wierzchołki danego 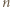 -kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że
-kąta wyznaczają średnicę tego okręgu, co z kolei przeczy założeniu, że 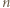 jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.
jest liczbą nieparzystą. Uzyskana sprzeczność kończy rozwiązanie zadania.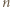 -kąta kolejnymi resztami z dzielenia przez
-kąta kolejnymi resztami z dzielenia przez 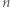 i zauważmy, że odcinki
i zauważmy, że odcinki 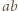 oraz
oraz 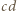 mają ten sam kolor wtedy i tylko wtedy, gdy
mają ten sam kolor wtedy i tylko wtedy, gdy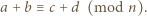
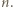
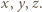 Trójkąt
Trójkąt 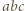 ma boki
ma boki 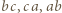 odpowiednio w tych kolorach wtedy i tylko wtedy, gdy
odpowiednio w tych kolorach wtedy i tylko wtedy, gdy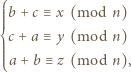
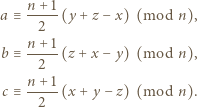
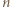 jest liczbą nieparzystą, więc trójka
jest liczbą nieparzystą, więc trójka 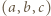 jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez
jest wyznaczona jednoznacznie z dokładnością do reszty z dzielenia przez 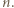
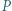 o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite
o współczynnikach całkowitych oraz względnie pierwsze dodatnie liczby całkowite 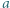 i
i 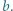 Udowodnić, że jeśli
Udowodnić, że jeśli 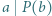 oraz
oraz 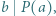 to
to 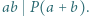
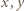 ma miejsce podzielność
ma miejsce podzielność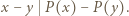
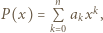 mamy
mamy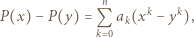
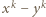 jest podzielna przez
jest podzielna przez 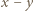 (w razie potrzeby przyjmujemy
(w razie potrzeby przyjmujemy 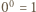 ).
).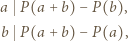
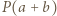 jest liczbą podzielną zarówno przez
jest liczbą podzielną zarówno przez 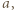 jak i przez
jak i przez 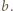 Pozostaje skorzystać z założenia, że liczby
Pozostaje skorzystać z założenia, że liczby 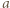 i
i 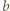 są względnie pierwsze.
są względnie pierwsze.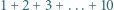 można zamienić niektóre znaki "
można zamienić niektóre znaki " 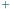 " na "
" na "  " w ten sposób, by wynik był równy
" w ten sposób, by wynik był równy 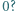
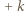 " na "
" na " 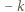 ", to wartość całego wyrażenia zmaleje o
", to wartość całego wyrażenia zmaleje o 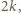 więc nie zmieni się jego parzystość. Początkowa suma jest nieparzysta, więc niemożliwe jest osiągnięcie wartości parzystej.
więc nie zmieni się jego parzystość. Początkowa suma jest nieparzysta, więc niemożliwe jest osiągnięcie wartości parzystej.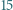 trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być
trzycyfrowych liczb pierwszych. Możemy zmazać dwie zapisane na tablicy liczby i zamiast nich zapisać wartość bezwzględną ich różnicy. Postępujemy tak aż do momentu, gdy na tablicy pozostanie jedna liczba. Czy tą liczbą może być 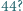
 i
i 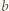 zastępujemy liczbą
zastępujemy liczbą 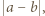 więc suma liczb na tablicy zmniejsza się o
więc suma liczb na tablicy zmniejsza się o 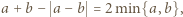 czyli nie zmienia się jej parzystość.
czyli nie zmienia się jej parzystość.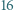 drzew, na każdym siedzi jeden wróbel. Wróble przelatują czasem na inne drzewa, ale zgodnie z regułą: dwa wróble lecą jednocześnie, każdy na drzewo sąsiadujące z tym, na którym siedział, jeden zgodnie, a drugi przeciwnie do ruchu wskazówek zegara. Czy jest możliwe, aby w pewnej chwili wszystkie wróble siedziały na tym samym drzewie?
drzew, na każdym siedzi jeden wróbel. Wróble przelatują czasem na inne drzewa, ale zgodnie z regułą: dwa wróble lecą jednocześnie, każdy na drzewo sąsiadujące z tym, na którym siedział, jeden zgodnie, a drugi przeciwnie do ruchu wskazówek zegara. Czy jest możliwe, aby w pewnej chwili wszystkie wróble siedziały na tym samym drzewie?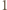 do
do 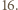 Każdemu wróblowi przypisujemy jego pozycję, czyli numer drzewa, na którym siedzi. Należy zauważyć, że suma pozycji wszystkich wróbli może się zmienić jedynie o wielokrotność
Każdemu wróblowi przypisujemy jego pozycję, czyli numer drzewa, na którym siedzi. Należy zauważyć, że suma pozycji wszystkich wróbli może się zmienić jedynie o wielokrotność 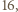 więc nie zmienia się jej reszta z dzielenia przez
więc nie zmienia się jej reszta z dzielenia przez 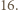
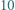 cukierków, drugie
cukierków, drugie 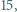 a trzecie
a trzecie 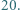 Każde z nich może w dowolnej chwili dać po jednym swoim cukierku pozostałej dwójce. Czy dzieląc się w ten sposób, dzieci mogą doprowadzić do tego, by każde z nich miało
Każde z nich może w dowolnej chwili dać po jednym swoim cukierku pozostałej dwójce. Czy dzieląc się w ten sposób, dzieci mogą doprowadzić do tego, by każde z nich miało 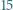 cukierków?
cukierków?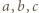 oznaczają liczby cukierków dzieci. Należy zauważyć, że wartość wyrażenia
oznaczają liczby cukierków dzieci. Należy zauważyć, że wartość wyrażenia 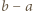 może się zmienić jedynie o wielokrotność
może się zmienić jedynie o wielokrotność 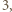 więc ma ono stałą resztę z dzielenia przez
więc ma ono stałą resztę z dzielenia przez 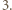
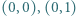 i
i 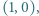 reguły postępowania takie jak w poprzednim zadaniu. Rozstrzygnąć, czy możliwe jest ustawienie pionków w wierzchołkach trójkąta, we wnętrzu którego znajduje się punkt o obu współrzędnych całkowitych.
reguły postępowania takie jak w poprzednim zadaniu. Rozstrzygnąć, czy możliwe jest ustawienie pionków w wierzchołkach trójkąta, we wnętrzu którego znajduje się punkt o obu współrzędnych całkowitych.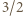 (dlaczego?).
(dlaczego?).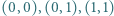 i
i 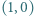 stoją pionki. Dozwolony ruch polega na wyborze dwóch pionków, a następnie przestawieniu jednego z nich na punkt płaszczyzny symetryczny względem punktu zajmowanego przez drugi pionek. Czy jest możliwe, aby po pewnej liczbie ruchów dwa pionki stanęły w tym samym miejscu?
stoją pionki. Dozwolony ruch polega na wyborze dwóch pionków, a następnie przestawieniu jednego z nich na punkt płaszczyzny symetryczny względem punktu zajmowanego przez drugi pionek. Czy jest możliwe, aby po pewnej liczbie ruchów dwa pionki stanęły w tym samym miejscu?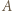 symetrycznie względem punktu
symetrycznie względem punktu 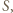 otrzymamy taki punkt
otrzymamy taki punkt 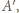 którego obie współrzędne są tej samej parzystości, co odpowiednie współrzędne punktu
którego obie współrzędne są tej samej parzystości, co odpowiednie współrzędne punktu 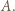
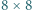 stoi pionek. Jeżeli na pierwszym i trzecim z trzech kolejnych pól leżących w jednym wierszu, kolumnie lub diagonali stoi co najmniej jeden pionek, to możemy wziąć z nich po jednym pionku i przełożyć na drugie z tych pól. Rozstrzygnąć, czy można, wykonując takie ruchy, przełożyć wszystkie pionki na jedno pole.
stoi pionek. Jeżeli na pierwszym i trzecim z trzech kolejnych pól leżących w jednym wierszu, kolumnie lub diagonali stoi co najmniej jeden pionek, to możemy wziąć z nich po jednym pionku i przełożyć na drugie z tych pól. Rozstrzygnąć, czy można, wykonując takie ruchy, przełożyć wszystkie pionki na jedno pole.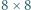 napisano liczbę 1, na A8 napisano -1, a na pozostałych polach 0. Możemy wielokrotnie wykonywać następującą operację: wybieramy dowolne pole i zmniejszamy napisaną na nim liczbę o liczbę pól sąsiednich (mających wspólny bok), zaś każdą z liczb napisanych na polach sąsiednich zwiększamy o 1. Rozstrzygnąć, czy można doprowadzić do stanu, w którym na wszystkich polach szachownicy napisana jest liczba 0.
napisano liczbę 1, na A8 napisano -1, a na pozostałych polach 0. Możemy wielokrotnie wykonywać następującą operację: wybieramy dowolne pole i zmniejszamy napisaną na nim liczbę o liczbę pól sąsiednich (mających wspólny bok), zaś każdą z liczb napisanych na polach sąsiednich zwiększamy o 1. Rozstrzygnąć, czy można doprowadzić do stanu, w którym na wszystkich polach szachownicy napisana jest liczba 0.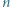 -kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor.
-kąta. Wykazać, że jego wierzchołki można tak pokolorować trzema kolorami, aby każde dwa punkty połączone bokiem lub jedną z narysowanych przekątnych miały różny kolor. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 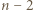 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce). -kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że
-kąta o tej własności, że w każdym wierzchołku tego trójkąta schodzi się nieparzysta liczba trójkątów tej triangulacji. Wykazać, że  jest liczbą podzielną przez 3.
jest liczbą podzielną przez 3. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 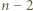 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).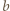 i
i 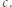
 -kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa
-kąta należą do trójkątów triangulacji tego samego koloru; bez straty ogólności przypuśćmy, że jest to kolor czarny. Tymczasem każda przekątna triangulacji jest bokiem dokładnie jednego trójkąta czarnego i jednego trójkąta białego. Stąd wniosek, że łączna liczba narysowanych przekątnych jest równa 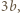 a łączna liczba boków
a łączna liczba boków  -kąta i narysowanych przekątnych jest równa
-kąta i narysowanych przekątnych jest równa 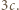 W konsekwencji
W konsekwencji 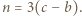
 -kąta, przy czym
-kąta, przy czym 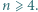 Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego
Na czarno malujemy wszystkie trójkąty tej triangulacji, których dokładnie jeden bok jest przekątną danego  -kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego
-kąta, a na biało - wszystkie trójkąty tej triangulacji, których wszystkie trzy boki są przekątnymi danego  -kąta. Wykazać, że liczba czarnych trójkątów jest o
-kąta. Wykazać, że liczba czarnych trójkątów jest o 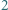 większa od liczby białych trójkątów.
większa od liczby białych trójkątów. -kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na
-kąta (niekoniecznie wypukłego) nazywamy podział tego wielokąta na 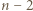 trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).
trójkąty przy użyciu pewnej liczby nieprzecinających się przekątnych (które mogą mieć wspólne końce).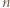 -kąta i oznaczmy przez
-kąta i oznaczmy przez 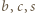 odpowiednio liczby białych, czarnych i szarych trójkątów.
odpowiednio liczby białych, czarnych i szarych trójkątów.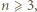 to nie istnieje trójkąt, którego wszystkie boki są także bokami danego
to nie istnieje trójkąt, którego wszystkie boki są także bokami danego  -kąta, więc każdy z
-kąta, więc każdy z 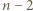 trójkątów został pomalowany dokładnie jednym kolorem, czyli
trójkątów został pomalowany dokładnie jednym kolorem, czyli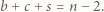
 -kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd
-kąta, a każdy szary trójkąt ma dokładnie jeden taki bok. Stąd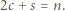
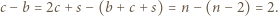
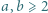 są liczbami naturalnymi, to liczby
są liczbami naturalnymi, to liczby 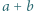 i
i 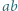 mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od
mają ten sam kolor. Dowieść, że wszystkie liczby naturalne większe od 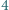 mają ten sam kolor.
mają ten sam kolor.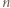 parzystych ten sam kolor mają liczby
parzystych ten sam kolor mają liczby  i
i 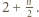 Dla
Dla 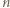 nieparzystych - liczby
nieparzystych - liczby 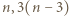 i
i 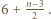
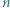 będzie liczbą naturalną. Udowodnić przez indukcję, że:
będzie liczbą naturalną. Udowodnić przez indukcję, że: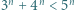 dla
dla 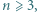 (b)
(b) 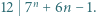
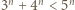 należy obustronnie pomnożyć przez 5. Otrzymamy wtedy nierówność, z której łatwo wydedukować tezę indukcyjną:
należy obustronnie pomnożyć przez 5. Otrzymamy wtedy nierówność, z której łatwo wydedukować tezę indukcyjną: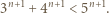
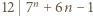 wynika, że
wynika, że 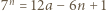 dla pewnego
dla pewnego 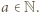 Mamy udowodnić, że
Mamy udowodnić, że 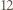 jest dzielnikiem liczby
jest dzielnikiem liczby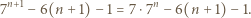
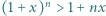 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych 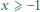 i liczb naturalnych
i liczb naturalnych 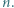
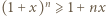 przez liczbę dodatnią
przez liczbę dodatnią 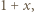 następnie wystarczy udowodnić, że
następnie wystarczy udowodnić, że 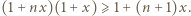
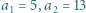 oraz
oraz 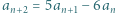 dla
dla 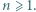 Wykazać, że
Wykazać, że 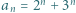 dla wszystkich naturalnych
dla wszystkich naturalnych 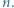
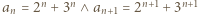 należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej
należy wykorzystać we wzorze rekurencyjnym z treści zadania w celu otrzymania tezy indukcyjnej 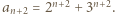
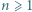 różnych okręgów dzieli płaszczyznę na co najwyżej
różnych okręgów dzieli płaszczyznę na co najwyżej 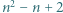 obszarów.
obszarów.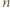 okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej
okręgów na płaszczyźnie, to po dorysowaniu jeszcze jednego liczba obszarów wzrośnie o co najwyżej 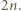
 będzie liczbą naturalną. Udowodnić, że szachownicę o wymiarach
będzie liczbą naturalną. Udowodnić, że szachownicę o wymiarach 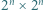 z jednym usuniętym polem można rozciąć na L-ki.
z jednym usuniętym polem można rozciąć na L-ki.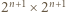 z usuniętym polem na
z usuniętym polem na 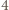 szachownice
szachownice 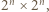 z których jedna ma usunięte pole. Aby móc zastosować założenie indukcyjne, potrzebujemy by wszystkie cztery je miały. W tym celu pierwszą L-kę należy wyciąć w odpowiedni sposób ze środka szachownicy
z których jedna ma usunięte pole. Aby móc zastosować założenie indukcyjne, potrzebujemy by wszystkie cztery je miały. W tym celu pierwszą L-kę należy wyciąć w odpowiedni sposób ze środka szachownicy