Zadanie ZM-1312
o zadaniu...
- Publikacja w Delcie: maj 2011
- Publikacja elektroniczna: 04-05-2011
Każdy punkt płaszczyzny pokolorowano na biało lub czarno. Udowodnić, że istnieje prostokąt o wierzchołkach pokolorowanych na ten sam kolor
Każdy punkt płaszczyzny pokolorowano na biało lub czarno. Udowodnić, że istnieje prostokąt o wierzchołkach pokolorowanych na ten sam kolor
Kot Bonifacy siedzi na pierwszym, najniższym szczeblu drabiny, kot Filemon na jedenastym. Grają w grę: na przemian przemieszczają się o jeden lub dwa szczeble, Bonifacy do góry, Filemon do dołu. Przegra ten, który nie będzie mógł wykonać ruchu (nie wolno przeskakiwać przeciwnika ani stawać na zajmowanym przez niego szczeblu). Zaczyna Bonifacy. Czy któryś kot może grać tak, by zapewnić sobie zwycięstwo?
Dwaj gracze ustawiają na przemian na szachownicy
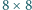 wieże,
tak by żadne dwie z nich się nie biły (wieża atakuje wszystkie pola
w swoim wierszu i w swojej kolumnie, gracze mają duży zapas wież).
Przegra ten z graczy, który jako pierwszy nie będzie mógł postawić
kolejnej wieży. Który gracz (rozpoczynający czy drugi) może zawsze
wygrać?
wieże,
tak by żadne dwie z nich się nie biły (wieża atakuje wszystkie pola
w swoim wierszu i w swojej kolumnie, gracze mają duży zapas wież).
Przegra ten z graczy, który jako pierwszy nie będzie mógł postawić
kolejnej wieży. Który gracz (rozpoczynający czy drugi) może zawsze
wygrać?
Na balu spotkało się
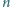 pań i
pań i
 panów, niektórzy są
zaznajomieni. Jakie warunki muszą być spełnione, by mogli dobrać się
do tańca w pary, w których się znają?
panów, niektórzy są
zaznajomieni. Jakie warunki muszą być spełnione, by mogli dobrać się
do tańca w pary, w których się znają?
Czy kasjer może wydać 20 zł siedmioma monetami o wartości 1 zł i 5 zł?
Czy istnieją różne liczby pierwsze
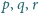 takie, że liczba
takie, że liczba

jest naturalna?
Zadanie zaproponował pan Tomasz Tkocz z Warszawy.
Udowodnić nierówność
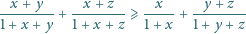
dla liczb
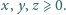
W nierównoramiennym trójkącie
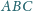 punkt
punkt
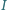 jest środkiem okręgu
wpisanego, stycznego do boków
jest środkiem okręgu
wpisanego, stycznego do boków
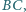
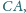
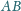 odpowiednio
w punktach
odpowiednio
w punktach
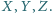 Proste
Proste
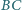 i
i
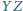 przecinają się
w punkcie
przecinają się
w punkcie
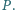 Dowieść, że proste
Dowieść, że proste
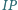 i
i
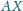 są
prostopadłe.
są
prostopadłe.
Kwadraty
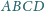 i
i
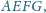 tak samo zorientowane, mają wspólny
tylko punkt
tak samo zorientowane, mają wspólny
tylko punkt
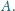 Wykaż, że
Wykaż, że
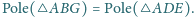
Na bokach
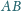 i
i
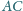 trójkąta
trójkąta
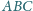 zbudowano, po jego
zewnętrznej stronie, kwadraty
zbudowano, po jego
zewnętrznej stronie, kwadraty
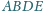 i
i
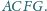 Punkty
Punkty
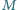 i
i
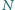 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
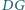 i
i
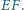 Wyznacz możliwe wartości wyrażenia
Wyznacz możliwe wartości wyrażenia
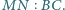
W trójkącie
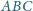 zachodzi równość
zachodzi równość
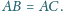 Punkt
Punkt
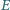 jest środkiem wysokości
jest środkiem wysokości
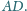 Punkt
Punkt
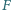 jest rzutem
prostokątnym punktu
jest rzutem
prostokątnym punktu
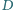 na prostą
na prostą
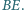 Udowodnij, że
Udowodnij, że
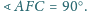
Punkt
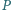 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
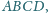 przy czym
przy czym
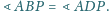 Wykaż, że
Wykaż, że
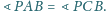
W sześciokącie wypukłym
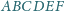 o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
o polu 1 przeciwległe boki są
równe i równoległe. Wyznacz pole trójkąta
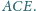
W trapezie
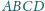 punkty
punkty
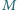 i
i
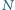 są środkami odpowiednio
ramion
są środkami odpowiednio
ramion
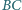 i
i
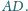 Wykaż, że
Wykaż, że
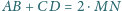 i że
i że

Dany jest trójkąt
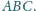 Wykaż, że z jego środkowych można
zbudować trójkąt.
Wykaż, że z jego środkowych można
zbudować trójkąt.
Dany jest trójkąt równoboczny
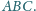 Punkty
Punkty
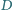 i
i
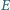 należą odpowiednio do boków
należą odpowiednio do boków
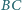 i
i
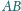 tego
trójkąta i
tego
trójkąta i
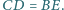 Punkt
Punkt
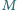 jest środkiem odcinka
jest środkiem odcinka
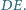 Udowodnij, że
Udowodnij, że
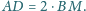
Trójkąt
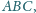 w którym
w którym
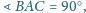 jest podstawą
ostrosłupa
jest podstawą
ostrosłupa
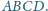 Ponadto zachodzą równości
Ponadto zachodzą równości
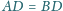 oraz
oraz
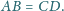 Wykaż, że
Wykaż, że
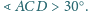
Dane jest słowo złożone z liter
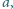
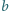 (np.
(np.
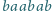 ). Na takim
słowie możemy wykonać następujące operacje:
). Na takim
słowie możemy wykonać następujące operacje:
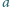 (np.
(np.
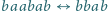 ),
),
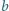 (np.
(np.
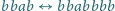 ),
),
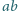 na
na
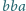 lub na odwrót
(np.
lub na odwrót
(np.
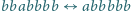 ).
).Rozstrzygnąć, czy za pomocą wielokrotnego wykonywania tych operacji można ze
słowa
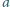 otrzymać słowo
otrzymać słowo
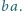
Na bokach
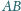 i
i
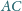 trójkąta
trójkąta
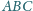 zbudowano po
zewnętrznej stronie podobne trójkąty prostokątne
zbudowano po
zewnętrznej stronie podobne trójkąty prostokątne
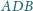 i
i
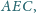 w
których kąty przy wierzchołkach
w
których kąty przy wierzchołkach
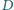 i
i
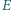 są proste. Punkt
są proste. Punkt
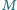 jest środkiem odcinka
jest środkiem odcinka
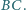 Udowodnić, że
Udowodnić, że
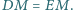
Znaleźć wszystkie liczby naturalne, których nie da się zapisać jako sumy co najmniej dwóch kolejnych liczb całkowitych dodatnich.
Zadanie zaproponował pan Witold Bednarek z Łodzi.
Niech
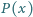 będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
będzie wielomianem stopnia dodatniego o współczynnikach
całkowitych. Wykazać, że dla każdej liczby naturalnej
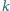 istnieje taka
liczba całkowita
istnieje taka
liczba całkowita
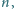 że liczba
że liczba
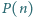 ma co najmniej
ma co najmniej
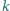 różnych dzielników pierwszych.
różnych dzielników pierwszych.
Szachownica o rozmiarach
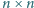 została pokryta płytkami
została pokryta płytkami
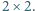 Każda płytka pokrywa dokładnie cztery pola. Płytki zachodzą na siebie, ale nie
wystają poza brzeg szachownicy. Liczba płytek przekracza
Każda płytka pokrywa dokładnie cztery pola. Płytki zachodzą na siebie, ale nie
wystają poza brzeg szachownicy. Liczba płytek przekracza
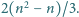 Dowieść, że można usunąć jedną płytkę tak, by pozostałe płytki nadal
pokrywały całą szachownicę.
Dowieść, że można usunąć jedną płytkę tak, by pozostałe płytki nadal
pokrywały całą szachownicę.
Funkcja
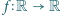 jest dana wzorem
jest dana wzorem
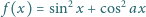
(dla pewnej stałej rzeczywistej
 ). Dowieść, że jeżeli
). Dowieść, że jeżeli
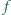 jest
funkcją okresową, to
jest
funkcją okresową, to
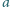 jest liczbą wymierną.
jest liczbą wymierną.
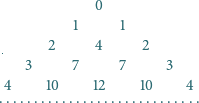
Diagram przedstawia początkowe wiersze nieskończonej tabeli trójkątnej.
Skrajnymi elementami kolejnych wierszy są kolejne liczby naturalne. Ponadto
obowiązuje reguła: jeśli liczby
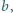
 są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
są sąsiednimi elementami
dowolnego wiersza, nad nimi znajduje się liczba
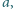 zaś pod nimi liczba
zaś pod nimi liczba
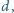 to
to
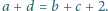 Udowodnić, że dla każdej liczby
całkowitej
Udowodnić, że dla każdej liczby
całkowitej
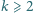 istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
istnieje nieskończenie wiele liczb, z których każda
występuje w tej tabeli dokładnie
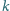 razy.
razy.
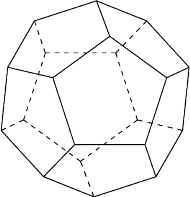
Dwunastościan foremny: 12 ścian, 30 krawędzi i 20 wierzchołków.
Krawędzie dwunastościanu foremnego (rys. 1) chcemy ponumerować
liczbami
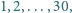 używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
używając każdej z nich dokładnie raz.
Rozstrzygnij, czy można to uczynić, tak aby suma numerów krawędzi
wychodzących z dowolnego wierzchołka była:
(a) parzysta;
(b) podzielna przez
4.
W wierzchołkach sześcianu napisano siedem zer i jedną jedynkę. Do każdej
z liczb na końcach dowolnej krawędzi można dodać 1. Czy wykonując szereg
takich operacji, można sprawić, by wszystkie liczby w wierzchołkach były
(a)
równe
(b) podzielne przez 3?
Zadanie pochodzi z broszury Przed konkursem matematycznym Stowarzyszenia na rzecz Edukacji Matematycznej (Wyd. Szkolne Omega, Kraków 2010).
Zadanie pochodzi z broszury Przed konkursem matematycznym Stowarzyszenia na rzecz Edukacji Matematycznej (Wyd. Szkolne Omega, Kraków 2010).
Na każdej ścianie sześcianu zapisano dodatnią liczbę całkowitą, a w każdym wierzchołku iloczyn liczb występujących na trzech ścianach z danym wierzchołkiem. Suma wszystkich liczb zapisanych w wierzchołkach tego sześcianu jest równa 2009. Jaka jest suma liczb zapisanych na jego ścianach?
Każdemu wierzchołkowi sześcianu przyporządkowano liczbę 1 lub
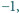 a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
a każdej ścianie – iloczyn liczb przyporządkowanych wierzchołkom tej
ściany. Wyznacz zbiór wartości, które może przyjąć suma 14 liczb
przyporządkowanych ścianom i wierzchołkom.
Dany jest czworościan foremny opisany na sferze o promieniu
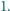 Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
Udowodnij, że w tym czworościanie można umieścić 6 kul o promieniu
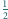 w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.
w taki sposób, aby każde dwie kule miały co najwyżej jeden punkt
wspólny.