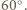Potęga punktu względem okręgu»Zadanie 6
o zadaniu...
- Zadanie pochodzi z artykułu Potęga punktu względem okręgu
- Publikacja w Delcie: listopad 2019
- Publikacja elektroniczna: 31 października 2019
- Artykuł źródłowy w wersji do druku [application/pdf]: (417 KB)
Punkt 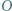 jest środkiem okręgu opisanego, a punkt
jest środkiem okręgu opisanego, a punkt 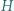 ortocentrum trójkąta ostrokątnego i różnobocznego
ortocentrum trójkąta ostrokątnego i różnobocznego 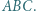 Punkty
Punkty 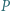 i
i 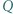 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach  i
i 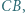 przy czym czworokąt
przy czym czworokąt 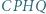 jest równoległobokiem. Wykazać, że
jest równoległobokiem. Wykazać, że 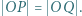
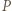 i
i 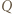 mają równą potęgę względem okręgu opisanego na trójkącie
mają równą potęgę względem okręgu opisanego na trójkącie  Do tego celu wystarczy podobieństwo odpowiednich trójkątów.
Do tego celu wystarczy podobieństwo odpowiednich trójkątów.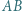 i prostopadła do niej cięciwa
i prostopadła do niej cięciwa 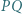 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 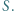 Okrąg
Okrąg 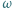 jest styczny (wewnętrznie) do okręgu
jest styczny (wewnętrznie) do okręgu  i do odcinków
i do odcinków 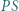 oraz
oraz 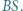 Niech
Niech 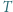 będzie punktem styczności okręgu
będzie punktem styczności okręgu 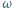 do odcinka
do odcinka 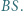 Wykazać, że
Wykazać, że 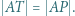
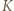 i
i 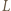 będą punktami styczności okręgu
będą punktami styczności okręgu 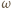 do, odpowiednio, okręgu
do, odpowiednio, okręgu  i odcinka
i odcinka  Wówczas punkty
Wówczas punkty 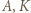 i
i 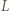 są współliniowe, gdyż punkt
są współliniowe, gdyż punkt 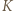 jest obrazem punktu
jest obrazem punktu 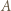 w jednokładności względem punktu
w jednokładności względem punktu 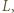 która przekształca okrąg
która przekształca okrąg  na
na 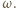 Mamy też
Mamy też 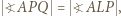 bo są to kąty wpisane, oparte na równej długości łukach okręgu
bo są to kąty wpisane, oparte na równej długości łukach okręgu  Resztę załatwia podobieństwo trójkątów i potęga punktu
Resztę załatwia podobieństwo trójkątów i potęga punktu 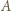 względem okręgu
względem okręgu 
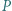 będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień
będzie wielomianem o współczynnikach wymiernych, który przyjmuje wartości niewymierne dla niewymiernych argumentów. Wykazać, że stopień 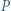 wynosi 1.
wynosi 1.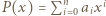 spełnia warunki zadania. Zauważmy, że możemy wybrać
spełnia warunki zadania. Zauważmy, że możemy wybrać 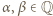 takie, że wielomian
takie, że wielomian 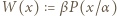 ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech
ma współczynniki całkowite oraz współczynnik przy najwyższej potędze wynosi 1. Niech 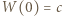 i niech
i niech 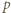 będzie liczbą pierwszą. Jeśli
będzie liczbą pierwszą. Jeśli 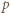 jest dostatecznie duże, to równanie
jest dostatecznie duże, to równanie 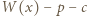 ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie
ma dokładnie jedno dodatnie rozwiązanie, które zgodnie z założeniem o wielomianie 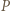 jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko
jest wymierne. Korzystając z twierdzenia o pierwiastkach wymiernych wielomianu o współczynnikach całkowitych dostajemy, że rozwiązaniem tym może być tylko 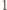 lub
lub  zatem dla dostatecznie dużych
zatem dla dostatecznie dużych 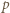 musi to być
musi to być  Wynika stąd, że
Wynika stąd, że 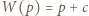 dla dostatecznie dużych liczb pierwszych
dla dostatecznie dużych liczb pierwszych  zatem
zatem 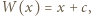 co oznacza, że
co oznacza, że 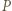 jest stopnia 1.
jest stopnia 1.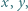 że
że 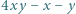 jest kwadratem liczby całkowitej.
jest kwadratem liczby całkowitej. dla pewnych liczb całkowitych
dla pewnych liczb całkowitych 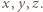 Równość tę możemy przepisać do postaci
Równość tę możemy przepisać do postaci 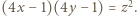 Niech
Niech  będzie dzielnikiem pierwszym
będzie dzielnikiem pierwszym 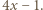 Wówczas
Wówczas 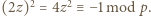 Z Małego Twierdzenia Fermata wiemy, że
Z Małego Twierdzenia Fermata wiemy, że 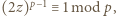 a zatem
a zatem 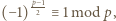 co oznacza że
co oznacza że 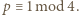 Ponieważ
Ponieważ 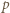 było dowolnym dzielnikiem pierwszym
było dowolnym dzielnikiem pierwszym 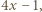 więc
więc 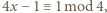 a to jest sprzeczność.
a to jest sprzeczność.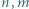 liczba rozwiązań nierówności
liczba rozwiązań nierówności 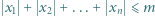 w liczbach całkowitych jest równa liczbie rozwiązań nierówności
w liczbach całkowitych jest równa liczbie rozwiązań nierówności 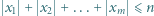 w liczbach całkowitych.
w liczbach całkowitych.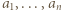 spełniają
spełniają 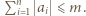 Możemy na dwa sposoby wskazać
Możemy na dwa sposoby wskazać 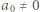 takie, że
takie, że  Każdy ciąg
Każdy ciąg 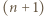 liczb spełniający tę równość (oraz
liczb spełniający tę równość (oraz  ) możemy podzielić na bloki, czyli fragmenty postaci
) możemy podzielić na bloki, czyli fragmenty postaci 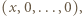 gdzie
gdzie 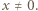 Jeśli długość takiego bloku to
Jeśli długość takiego bloku to 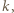 to przyporządkujemy mu blok
to przyporządkujemy mu blok 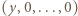 długości
długości 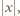 gdzie
gdzie 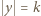 oraz
oraz 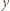 jest tego samego znaku, co
jest tego samego znaku, co 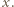 Wykonując tę operację na wszystkich blokach, dostaniemy ciąg
Wykonując tę operację na wszystkich blokach, dostaniemy ciąg 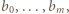 gdzie
gdzie 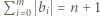 i
i  co daje nam ciąg liczb całkowitych
co daje nam ciąg liczb całkowitych 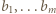 spełniający
spełniający  Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.
Nietrudno przekonać się, że przedstawione przekształcenie jest wzajemnie jednoznaczne, co kończy rozwiązanie.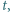 dla której nierówność
dla której nierówność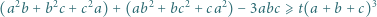
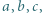 będących długościami boków trójkąta.
będących długościami boków trójkąta.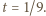 Wykażemy, że wartość
Wykażemy, że wartość 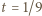 gwarantuje spełnienie nierówności dla każdego trójkąta.
gwarantuje spełnienie nierówności dla każdego trójkąta.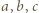 dowolnego trójkąta można wyrazić przez trójkę liczb
dowolnego trójkąta można wyrazić przez trójkę liczb  pisząc:
pisząc: 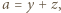
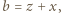
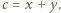 Oznaczmy przez
Oznaczmy przez 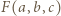 różnicę między lewą oraz prawą stroną zadanej nierówności (z parametrem
różnicę między lewą oraz prawą stroną zadanej nierówności (z parametrem 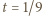 ); mamy uzasadnić, że
); mamy uzasadnić, że 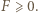 Do dowodu użyjemy tożsamości
Do dowodu użyjemy tożsamości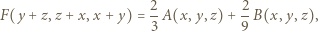
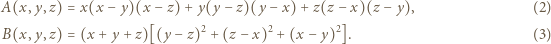
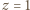 oraz czterech różnych wartości
oraz czterech różnych wartości 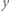 (można też użyć programu komputerowego). Wyrażenia (2) i (3) mają dla
(można też użyć programu komputerowego). Wyrażenia (2) i (3) mają dla 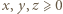 wartości nieujemne: nierówność
wartości nieujemne: nierówność 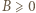 jest oczywista; zaś
jest oczywista; zaś 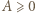 to znana nierówność Schura. Stąd
to znana nierówność Schura. Stąd 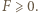 Wniosek: szukana maksymalna wartość
Wniosek: szukana maksymalna wartość  wynosi
wynosi 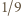 .
.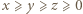 ; wówczas
; wówczas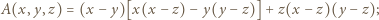
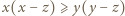 .
. będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru
będzie dowolnym niepustym skończonym zbiorem liczb całkowitych. Dowieść, że można ustawić elementy zbioru 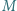 w ciąg
w ciąg 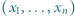 tak, by dla każdej trójki wskaźników
tak, by dla każdej trójki wskaźników 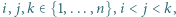 spełniony był warunek:
spełniony był warunek: 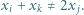
 o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru
o dowolną liczbę całkowitą. Można więc zakładać, że jego elementami są liczby nieujemne. Zauważmy też, że jeśli elementy pewnego zbioru  da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru
da się uporządkować w wymagany sposób, wówczas to samo uporządkowanie jest dobre dla każdego podzbioru zbioru 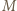 (po wykreśleniu zbędnych elementów).
(po wykreśleniu zbędnych elementów).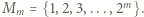 Dla
Dla 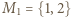 każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego
każde z dwóch uporządkowań jest dobre (warunek spełniony "w próżni"). Dalej indukcja: przyjmijmy, że dla pewnego 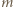 zbiór
zbiór 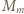 daje się ustawić w ciąg
daje się ustawić w ciąg 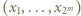 tak, że
tak, że 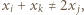 gdy
gdy 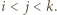 Wówczas ciąg
Wówczas ciąg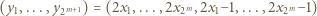
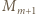 (jednym z możliwych); bo gdy
(jednym z możliwych); bo gdy 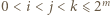 lub
lub 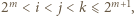 nierówność
nierówność 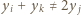 wynika z założenia indukcyjnego; gdy zaś
wynika z założenia indukcyjnego; gdy zaś  liczba
liczba 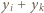 jest nieparzysta, więc
jest nieparzysta, więc 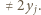 To kończy krok indukcyjny.
To kończy krok indukcyjny. i
i 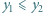 spełniają równości
spełniają równości  oraz
oraz 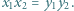 Udowodnić, że
Udowodnić, że 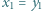 i
i 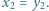
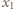 i
i  są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby
są, na mocy wzorów Viete'a, pierwiastkami tego samego trójmianu kwadratowego, co liczby 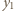 oraz
oraz 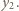
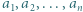 będą ustalonymi liczbami rzeczywistymi. Dla jakiego
będą ustalonymi liczbami rzeczywistymi. Dla jakiego 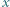 wartość funkcji
wartość funkcji
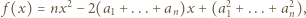
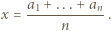
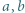 i
i  spełniają nierówność
spełniają nierówność 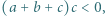 przy czym
przy czym 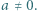 Wykazać, że
Wykazać, że 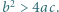
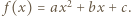 Wówczas mamy
Wówczas mamy  więc funkcja
więc funkcja 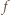 przyjmuje zarówno dodatnie i ujemne wartości, skąd
przyjmuje zarówno dodatnie i ujemne wartości, skąd 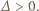
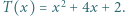

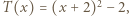

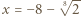
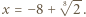
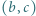
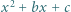
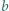
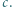
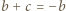
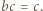
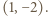


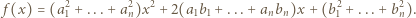
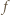 przyjmuje wyłącznie wartości nieujemne, więc
przyjmuje wyłącznie wartości nieujemne, więc 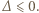 Jest to nierówność równoważna dowodzonej.
Jest to nierówność równoważna dowodzonej.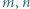 oraz
oraz 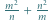 są całkowite. Udowodnić, że liczba
są całkowite. Udowodnić, że liczba 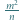 również jest całkowita.
również jest całkowita.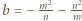 oraz
oraz  Liczby
Liczby 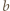 i
i  są całkowite, zaś liczby wymierne
są całkowite, zaś liczby wymierne  i
i  są pierwiastkami trójmianu (unormowanego)
są pierwiastkami trójmianu (unormowanego) 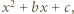 więc są całkowite.
więc są całkowite.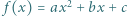 spełnia dla każdego
spełnia dla każdego ![|x∈ [−1,1]](/math/temat/matematyka/analiza/zadania/2019/09/30/zm-19_10-kpo-8/2x-74a6438c69d0f6ea8ca78cf3a770b01ff3c09138-im-2C,6B,73-FF,FF,FF.gif) nierówność
nierówność 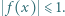 Wyznaczyć największą możliwą wartość wyrażenia
Wyznaczyć największą możliwą wartość wyrażenia 
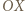 i
i  można założyć bez utraty ogólności, że
można założyć bez utraty ogólności, że 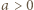 i
i 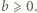 Jeśli
Jeśli  to
to 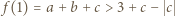 oraz
oraz 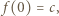 więc
więc 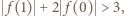 czyli
czyli 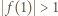 lub
lub 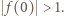 Wartość
Wartość  jest osiągalna, na przykład dla funkcji
jest osiągalna, na przykład dla funkcji 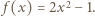
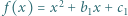 i
i  których współczynniki są rzeczywiste i spełniają warunek
których współczynniki są rzeczywiste i spełniają warunek
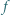 i
i 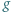 mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.
mają obydwa pierwiastki rzeczywiste, a każdy z nich ma jeden pierwiastek leżący na osi liczbowej pomiędzy pierwiastkami drugiego.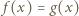 ma dokładnie jedno rozwiązanie
ma dokładnie jedno rozwiązanie 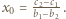 Wówczas
Wówczas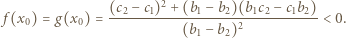
 i
i  przecinają się tylko w jednym punkcie, leżącym poniżej osi
przecinają się tylko w jednym punkcie, leżącym poniżej osi  Resztę załatwia własność Darboux.
Resztę załatwia własność Darboux. jest cyfrą setek,
jest cyfrą setek,  - cyfrą dziesiątek, a
- cyfrą dziesiątek, a  - cyfrą jedności, jest pierwsza. Dowieść, że
- cyfrą jedności, jest pierwsza. Dowieść, że 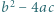 nie jest kwadratem liczby naturalnej.
nie jest kwadratem liczby naturalnej.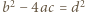 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 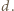 Niech
Niech 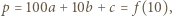 gdzie
gdzie 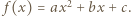 Korzystając z postaci iloczynowej, otrzymamy po przekształceniach
Korzystając z postaci iloczynowej, otrzymamy po przekształceniach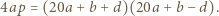
 jest pierwsza, więc dzieli co najmniej jedną z liczb:
jest pierwsza, więc dzieli co najmniej jedną z liczb: 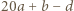 lub
lub 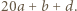 Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od
Tu mamy sprzeczność, bo są to liczby dodatnie mniejsze od 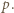
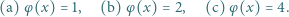
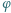 oznacza funkcję Eulera.
oznacza funkcję Eulera.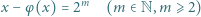
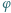 oznacza funkcję Eulera.
oznacza funkcję Eulera.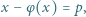
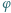 jest funkcją Eulera, a
jest funkcją Eulera, a 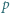 jest daną liczbą pierwszą. Wykazać, że równanie (*):
jest daną liczbą pierwszą. Wykazać, że równanie (*): ).
). kart oznaczonych liczbami
kart oznaczonych liczbami  ułożonych w losowej kolejności. Wielokrotnie wykonujemy następującą operację: Jeśli karta na górze stosu ma numer
ułożonych w losowej kolejności. Wielokrotnie wykonujemy następującą operację: Jeśli karta na górze stosu ma numer 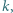 to odwracamy kolejność wierzchnich
to odwracamy kolejność wierzchnich 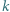 kart. Wykazać, że w końcu na górze pojawi się karta o numerze
kart. Wykazać, że w końcu na górze pojawi się karta o numerze 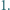
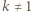 raz pojawi się na górze stosu, to aby pojawiła się tam ponownie, wcześniej musi się tam znaleźć liczba większa od
raz pojawi się na górze stosu, to aby pojawiła się tam ponownie, wcześniej musi się tam znaleźć liczba większa od 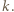 W szczególności
W szczególności 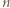 pojawi się na górze co najwyżej raz. Jeśli to nastąpi, to
pojawi się na górze co najwyżej raz. Jeśli to nastąpi, to 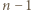 pojawi się później co najwyżej raz, jeżeli nie, to
pojawi się później co najwyżej raz, jeżeli nie, to  również pojawi się w ogóle co najwyżej raz. Po ewentualnym wystąpieniu
również pojawi się w ogóle co najwyżej raz. Po ewentualnym wystąpieniu 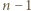 liczba
liczba 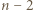 pojawi się co najwyżej raz itd. To oznacza, że w pewnym momencie na górze musi pojawić się liczba
pojawi się co najwyżej raz itd. To oznacza, że w pewnym momencie na górze musi pojawić się liczba 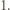
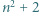 oraz
oraz  dla pewnej liczby naturalnej
dla pewnej liczby naturalnej 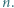
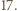
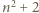 oraz
oraz 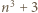 dzieli również liczbę
dzieli również liczbę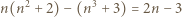
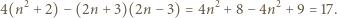
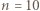 mamy
mamy 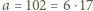 oraz
oraz 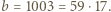
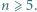 Wykazać, że elementy zbioru
Wykazać, że elementy zbioru 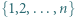 można tak pokolorować na czerwono i niebiesko, że suma czerwonych liczb jest równa iloczynowi niebieskich liczb.
można tak pokolorować na czerwono i niebiesko, że suma czerwonych liczb jest równa iloczynowi niebieskich liczb. jest liczbą nieparzystą, czyli
jest liczbą nieparzystą, czyli  dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 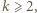 to na niebiesko malujemy liczby
to na niebiesko malujemy liczby 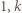 oraz
oraz  a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa
a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa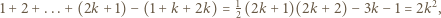
 jest liczbą parzystą, czyli
jest liczbą parzystą, czyli 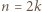 dla pewnej liczby całkowitej
dla pewnej liczby całkowitej 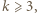 to na niebiesko malujemy liczby
to na niebiesko malujemy liczby 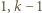 oraz
oraz 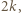 a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa
a na czerwono - wszystkie pozostałe. Wówczas suma czerwonych liczb jest równa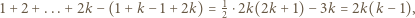
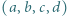 o tej własności, że każdy z iloczynów
o tej własności, że każdy z iloczynów 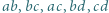 jest o 1 większy od kwadratu pewnej liczby naturalnej.
jest o 1 większy od kwadratu pewnej liczby naturalnej.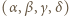 jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka
jest dowolną czwórką kolejnych liczb naturalnych nieparzystych, wówczas czwórka 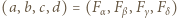 jest dobra; jak zwykle,
jest dobra; jak zwykle, 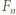 oznacza
oznacza  -tą liczbę Fibonacciego (
-tą liczbę Fibonacciego ( 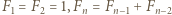 dla
dla  ).
). do pełnego bloku siedmiu kolejnych liczb naturalnych
do pełnego bloku siedmiu kolejnych liczb naturalnych  i korzystamy ze znanych tożsamości
i korzystamy ze znanych tożsamości
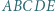 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 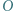 ; przy tym
; przy tym 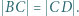 Przekątne
Przekątne 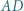 i
i  są prostopadłe, zaś przekątne
są prostopadłe, zaś przekątne 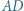 i
i  przecinają się w takim punkcie
przecinają się w takim punkcie 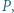 że
że 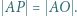 Wykazać, że trójkąt
Wykazać, że trójkąt  jest równoboczny.
jest równoboczny.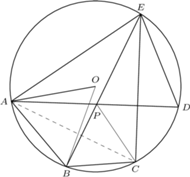
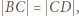 punkt
punkt  jest środkiem łuku
jest środkiem łuku  ; zatem prosta
; zatem prosta 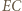 jest dwusieczną kąta wpisanego
jest dwusieczną kąta wpisanego 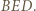 Przy tym jest prostopadła do prostej
Przy tym jest prostopadła do prostej 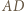 ; jest więc symetralną odcinka
; jest więc symetralną odcinka 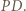 Stąd wynika, że
Stąd wynika, że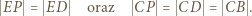
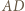 i
i 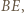 przecinające się w punkcie
przecinające się w punkcie 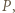 wyznaczają trójkąty podobne:
wyznaczają trójkąty podobne:  ; a ponieważ
; a ponieważ 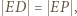 zatem
zatem 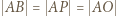 (ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt
(ostatnia równość jest dana w założeniach). To pokazuje, że trójkąt 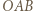 jest równoboczny, wobec czego
jest równoboczny, wobec czego  W takim razie
W takim razie 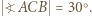
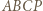 to deltoid
to deltoid 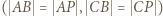 ; stąd
; stąd 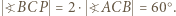 Wobec wcześniejszego spostrzeżenia, że
Wobec wcześniejszego spostrzeżenia, że 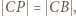 dostajemy tezę zadania: trójkąt
dostajemy tezę zadania: trójkąt  jest równoboczny.
jest równoboczny.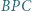 i
i 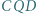 są równoboczne i leżą na zewnątrz równoległoboku
są równoboczne i leżą na zewnątrz równoległoboku 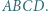 Udowodnić, że trójkąt
Udowodnić, że trójkąt 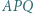 też jest równoboczny.
też jest równoboczny.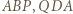 i
i 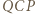 są przystające (bkb).
są przystające (bkb).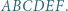 Punkty
Punkty 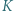 i
i 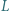 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 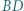 i
i 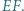 Dowieść, że trójkąt
Dowieść, że trójkąt 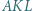 jest równoboczny.
jest równoboczny.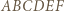 na
na  przystające trójkąty równoboczne można zauważyć, że odcinki
przystające trójkąty równoboczne można zauważyć, że odcinki  są dłuższymi przekątnymi przystających równoległoboków
są dłuższymi przekątnymi przystających równoległoboków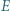 i
i 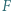 leżą odpowiednio na bokach
leżą odpowiednio na bokach 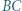 i
i 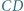 prostokąta
prostokąta 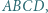 przy czym trójkąt
przy czym trójkąt 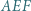 jest równoboczny. Punkt
jest równoboczny. Punkt 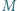 jest środkiem odcinka
jest środkiem odcinka 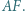 Wykazać, że trójkąt
Wykazać, że trójkąt 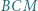 jest równoboczny.
jest równoboczny. i
i 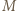 leżą na okręgu o średnicy
leżą na okręgu o średnicy 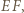 więc
więc 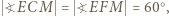 analogicznie
analogicznie 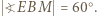
 i
i 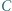 leżą kolejno na prostej
leżą kolejno na prostej  Punkty
Punkty 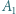 i
i 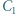 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 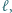 przy czym trójkąty
przy czym trójkąty  i
i 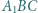 są równoboczne. Punkty
są równoboczne. Punkty 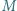 i
i 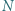 są środkami odcinków odpowiednio
są środkami odcinków odpowiednio 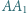 i
i 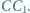 Udowodnić, że trójkąt
Udowodnić, że trójkąt 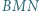 jest równoboczny.
jest równoboczny.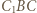 wokół punktu
wokół punktu 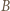 o
o 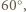 otrzymamy trójkąt
otrzymamy trójkąt 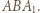 Obrazem punktu
Obrazem punktu 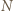 w tym obrocie jest punkt
w tym obrocie jest punkt  więc
więc  i
i 
 i punkt
i punkt 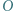 wewnątrz niego, przy czym zachodzą równości:
wewnątrz niego, przy czym zachodzą równości: 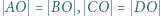 i
i  Dowieść, że środki odcinków
Dowieść, że środki odcinków 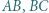 i
i 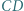 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.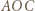 o
o 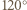 wokół punktu
wokół punktu 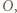 otrzymamy trójkąt
otrzymamy trójkąt 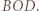 Zatem te trójkąty są przystające oraz proste
Zatem te trójkąty są przystające oraz proste 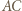 i
i 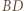 przecinają się pod kątem
przecinają się pod kątem