Zadanie ZM-1579
o zadaniu...
- Publikacja w Delcie: październik 2018
- Publikacja elektroniczna: 1 października 2018
Zadanie 768 zaproponował pan Witold Bednarek z Łodzi.
Znaleźć wszystkie trójki liczb naturalnych 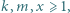 spełniające równanie
spełniające równanie
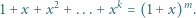 |
Kwadrat o boku długości 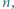 będącej liczbą naturalną, został podzielony prostymi poziomymi i pionowymi na
będącej liczbą naturalną, został podzielony prostymi poziomymi i pionowymi na 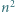 kwadracików jednostkowych. Powstała siatka, utworzona z
kwadracików jednostkowych. Powstała siatka, utworzona z 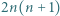 odcinków jednostkowych (boków tych kwadracików). Używając czterech barw, należy te odcinki pokolorować (każdy odcinek jednym kolorem) tak, żeby każdy kwadracik jednostkowy miał boki różnych kolorów oraz by każdy bok dużego kwadratu uzyskał jednolity kolor - ale każdy inny. Dla jakich liczb naturalnych
odcinków jednostkowych (boków tych kwadracików). Używając czterech barw, należy te odcinki pokolorować (każdy odcinek jednym kolorem) tak, żeby każdy kwadracik jednostkowy miał boki różnych kolorów oraz by każdy bok dużego kwadratu uzyskał jednolity kolor - ale każdy inny. Dla jakich liczb naturalnych 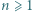 jest to wykonalne?
jest to wykonalne?
Jak wygrać (lub zremisować) w szachy z arcymistrzem, nawet nie umiejąc grać?
Znajdź dowolną trójkę dodatnich liczb całkowitych 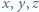 spełniających równanie
spełniających równanie
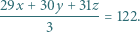
Czy istnieją takie liczby niewymierne 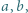 dla których liczba
dla których liczba 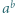 jest wymierna?
jest wymierna?
Jeśli szerokość pewnego prostokąta powiększyć o 50%, to jego szerokość powiększy się o 25%. O ile procent zmniejszy się długość tego prostokąta, jeśli jego długość zmniejszymy o 50%?
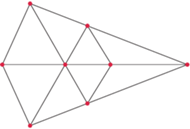
Za pojedynczą drogę uważamy całą prostą, np. droga pozioma łączy cztery miasta.
Planszą do gry w Jam jest mapa pewnego kraju, w którym jest 8 miast i 9 prostych dróg przez nie. Dwaj gracze na przemian malują, każdy swoim kolorem, po jednej całej drodze. Wygrywa ten, kto pierwszy pomaluje swoim kolorem wszystkie drogi przez któreś miasto. Jak grać, żeby wygrać?
Rozważamy trójkąt równoboczny 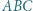 o boku
o boku 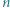 podzielony na
podzielony na 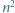 trójkątów równobocznych o boku
trójkątów równobocznych o boku 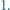 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 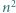 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę równoległoboków o wierzchołkach w węzłach, których dwa boki są równoległe do 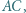 a dwa do
a dwa do 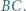
Rozważamy trójkąt równoboczny 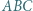 o boku
o boku 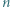 podzielony na
podzielony na 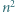 trójkątów równobocznych o boku
trójkątów równobocznych o boku 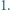 Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych
Każdy punkt, który jest wierzchołkiem co najmniej jednego z tych 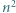 trójkątów, nazwijmy węzłem.
trójkątów, nazwijmy węzłem.
Wyznaczyć liczbę trójkątów równobocznych o wierzchołkach w węzłach (ale bokach niekoniecznie równoległych do boków 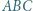 ).
).
Mając daną siatkę czworościanu, skonstruować punkty styczności sfery wpisanej w ten czworościan do jego ścian.
Zadanie 766 zaproponował pan Piotr Kumor z Olsztyna.
Znaleźć liczbę rzeczywistą 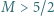 taką, że dla dowolnych liczb dodatnich
taką, że dla dowolnych liczb dodatnich 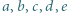 zachodzi nierówność
zachodzi nierówność
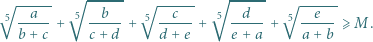 |
Im większa liczba 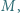 tym lepsze rozwiązanie.
tym lepsze rozwiązanie.
Czworokąt 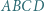 jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek
jest wpisany w okrąg. Jego najmniejszy kąt wewnętrzny ma wierzchołek 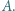 Zakładamy, że proste
Zakładamy, że proste 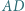 i
i 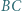 przecinają się w punkcie
przecinają się w punkcie 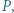 zaś proste
zaś proste 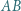 i
i 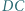 przecinają się w punkcie
przecinają się w punkcie 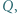 przy czym
przy czym 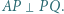 Niech
Niech 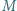 będzie środkiem przekątnej
będzie środkiem przekątnej 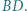 Wykazać, że
Wykazać, że 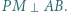
Na okręgu umieszczono 101 dodatnich liczb całkowitych o sumie równej 300. Wykaż, że istnieje taki łuk okręgu, na którym suma liczb równa jest 200.
Wykaż, że wśród dowolnych 1111 parami różnych podzbiorów zbioru 11-elementowego zawsze znajdą się dwa rozłączne.
Udowodnij, że w dowolnym ciągu 2018 liczb całkowitych zawsze można wskazać pewną liczbę kolejnych wyrazów, których suma jest podzielna przez 2018.
Podczas defilady żołnierze mają być ustawieni w prostokąt, przy czym w każdej kolumnie i w każdym rzędzie mają stać od najwyższego do najniższego (żadni dwaj z nich nie są równego wzrostu). Dowódca ustawia ich w prostokącie jakkolwiek, po czym porządkuje według wzrostu w każdej kolumnie osobno, następnie zaś w każdym rzędzie (psując być może porządek w kolumnach), potem, jeśli trzeba, znów w kolumnach, znowu w rzędach etc. Czy ten sposób działania ma sens, tzn. czy niezależnie od początkowego ustawienia żołnierzy ta procedura zawsze po skończenie wielu takich przestawieniach da żądany efekt? A jeśli tak, to po ilu?
W szeregu stoi, w przypadkowej kolejności, 50 żołnierzy. Żadnych dwóch nie jest tego samego wzrostu. Wykaż, że można wybrać ośmiu z nich tak, aby, gdy wystąpią oni krok naprzód, byli ustawieni według wzrostu (rosnąco lub malejąco).
Wykaż, że dla każdej liczby całkowitej 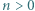 istnieje taka liczba całkowita
istnieje taka liczba całkowita 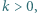 że liczbę
że liczbę 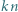 można zapisać w systemie dziesiętnym używając wyłącznie cyfr 0 i 1.
można zapisać w systemie dziesiętnym używając wyłącznie cyfr 0 i 1.
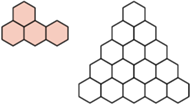
Płytką nazwiemy pokazaną na rysunku figurę złożoną z czterech sześciokątów foremnych o boku 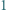 oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei
oraz dowolną figurę otrzymaną z niej przez obrót lub symetrię. Z kolei 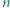 -trójkątem nazwiemy trójkątny układ tworzony przez
-trójkątem nazwiemy trójkątny układ tworzony przez 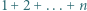 sześciokątów foremnych o boku
sześciokątów foremnych o boku 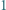 (na rysunku pokazano
(na rysunku pokazano 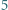 -trójkąt). Znaleźć wszystkie dodatnie liczby całkowite
-trójkąt). Znaleźć wszystkie dodatnie liczby całkowite 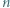 o tej własności, że z pewnej liczby płytek można ułożyć
o tej własności, że z pewnej liczby płytek można ułożyć 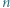 -trójkąt.
-trójkąt.
Dodatnią liczbę całkowitą  nazwiemy podkwadratową, jeżeli
nazwiemy podkwadratową, jeżeli 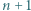 jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.
jest kwadratem liczby całkowitej. Wykazać, że istnieje nieskończenie wiele par liczb podkwadratowych o tej własności, że ich suma oraz iloczyn także są podkwadratowe.
Wewnątrz kwadratu jednostkowego 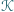 znajduje się wielokąt wypukły
znajduje się wielokąt wypukły 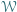 o polu większym od
o polu większym od 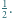 Wykazać, że wewnątrz wielokąta
Wykazać, że wewnątrz wielokąta 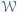 można wskazać odcinek o długości
można wskazać odcinek o długości  równoległy do boku kwadratu
równoległy do boku kwadratu 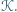
Wykaż, że środkowa dzieli trójkąt na dwa trójkąty o równych polach.
Wykaż, że środkowe dzielą trójkąt na sześć trójkątów o równych polach.
Punkt 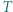 należy do wnętrza trójkąta
należy do wnętrza trójkąta 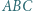 oraz
oraz 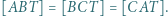 Wykaż, że
Wykaż, że 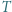 jest środkiem ciężkości trójkąta
jest środkiem ciężkości trójkąta 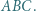
Dany jest równoległobok 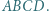 Punkty
Punkty 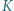 i
i 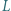 są środkami boków
są środkami boków 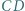 i
i 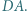 Proste
Proste 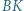 i
i 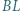 przecinają przekątną
przecinają przekątną 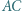 odpowiednio w punktach
odpowiednio w punktach 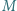 i
i 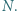 Wykaż, że
Wykaż, że ![1 ]+[BMN]+[CKM]=3[ABCD] |[ALN](/math/temat/matematyka/geometria/planimetria/zadania/2018/07/24/zm-18_08-deltoid-6/11x-a985b0af3fbf2b8f27676b5a2afc831fe04a782f-im-2C,6B,73-FF,FF,FF.gif) oraz że
oraz że 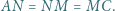
Wykaż, że ze środkowych dowolnego trójkąta można zbudować trójkąt.