Zadanie ZM-1469
o zadaniu...
- Publikacja w Delcie: wrzesień 2015
- Publikacja elektroniczna: 31-08-2015
Udowodnić, że dla dodatnich liczb 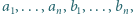 spełniających
spełniających 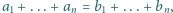 prawdziwa jest nierówność
prawdziwa jest nierówność
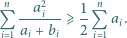
Udowodnić, że dla dodatnich liczb 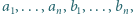 spełniających
spełniających 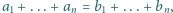 prawdziwa jest nierówność
prawdziwa jest nierówność
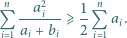
Zadanie 706 zaproponował pan Witold Bednarek z Łodzi.
Wyznaczyć wszystkie liczby naturalne 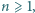 dla których istnieje wielomian
dla których istnieje wielomian 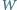 stopnia
stopnia 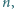 o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie
o współczynnikach całkowitych, ze współczynnikiem wiodącym równym 1, i taki, że równanie 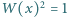 ma
ma 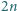 pierwiastków całkowitych (niekoniecznie różnych).
pierwiastków całkowitych (niekoniecznie różnych).
Niech 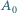 będzie ustalonym wierzchołkiem
będzie ustalonym wierzchołkiem 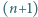 -kąta foremnego. Numerujemy pozostałe wierzchołki
-kąta foremnego. Numerujemy pozostałe wierzchołki 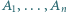 w dowolnej kolejności. Każdemu bokowi
w dowolnej kolejności. Każdemu bokowi 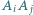 przyporządkowujemy liczbę
przyporządkowujemy liczbę 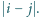 Niech
Niech 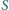 będzie sumą
będzie sumą 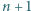 liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej
liczb, przyporządkowanych wszystkim bokom. Dla zadanej liczby naturalnej  :
:
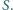
 wierzchołków (poza
wierzchołków (poza 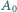 ), przy których
), przy których 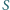 osiąga ową minimalną wartość.
osiąga ową minimalną wartość.Niech 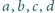 będą takimi liczbami rzeczywistymi, że
będą takimi liczbami rzeczywistymi, że

Wykazać, że 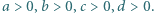
Udowodnić, że liczba

jest niewymierna.
Rozważmy zbiór

złożony z 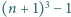 punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór
punktów w przestrzeni. Wyznaczyć minimalną liczbę płaszczyzn, których suma mnogościowa zawiera zbiór 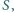 ale nie zawiera punktu
ale nie zawiera punktu 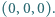
Niech 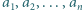 oraz
oraz 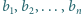 będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci
będą dwoma różnymi (czyli różniącymi się nie tylko porządkiem) zestawami liczb całkowitych dodatnich. Udowodnić, że jeżeli zestaw liczb postaci 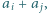 gdzie
gdzie 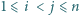 pokrywa się z zestawem
pokrywa się z zestawem 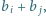 dla
dla 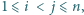 to
to 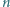 jest potęgą liczby 2.
jest potęgą liczby 2.
Liczby rzeczywiste 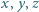 spełniają warunki
spełniają warunki

Udowodnić, że 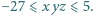
Dane jest 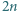 parami różnych liczb rzeczywistych
parami różnych liczb rzeczywistych 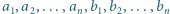 oraz tablica
oraz tablica 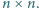 W pole leżące w
W pole leżące w 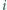 -tym wierszu i w
-tym wierszu i w 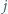 -tej kolumnie wpisano liczbę
-tej kolumnie wpisano liczbę 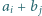 dla
dla 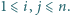 Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Udowodnić, że jeżeli iloczyny liczb we wszystkich kolumnach są równe, to również iloczyny liczb we wszystkich wierszach są równe.
Okrąg wpisany w trójkąt 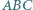 jest styczny do boków
jest styczny do boków 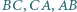 odpowiednio w punktach
odpowiednio w punktach 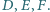 Prosta równoległa do
Prosta równoległa do 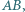 przechodząca przez punkt
przechodząca przez punkt 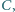 przecina proste
przecina proste 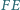 i
i 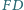 odpowiednio w punktach
odpowiednio w punktach 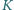 i
i 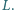 Udowodnij, że na czworokącie
Udowodnij, że na czworokącie 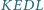 można opisać okrąg.
można opisać okrąg.
Czworokąt 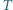 jest wpisany w okrąg
jest wpisany w okrąg 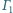 oraz opisany na okręgu
oraz opisany na okręgu 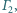 przy czym
przy czym 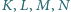 są kolejnymi punktami styczności
są kolejnymi punktami styczności 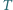 z
z 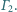 Wykaż, że
Wykaż, że 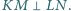
Dany jest kwadrat 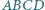 i taki punkt
i taki punkt 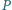 w jego wnętrzu, dla którego
w jego wnętrzu, dla którego 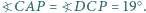 Wyznacz
Wyznacz 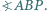
Okrąg 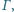 wpisany w trójkąt
wpisany w trójkąt 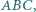 jest styczny do boków
jest styczny do boków 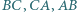 odpowiednio w punktach
odpowiednio w punktach 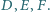 Wykaż, że środki
Wykaż, że środki 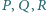 okręgów wpisanych w trójkąty
okręgów wpisanych w trójkąty 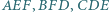 leżą na okręgu
leżą na okręgu 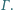
Udowodnij twierdzenie o stycznej i cięciwie oraz twierdzenie odwrotne.
Dwa okręgi przecinają się w punktach 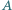 i
i 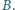 Proste styczne do tych okręgów w punkcie
Proste styczne do tych okręgów w punkcie 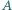 przecinają je w drugich punktach
przecinają je w drugich punktach 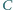 i
i 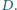 Wykaż, że
Wykaż, że 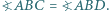
Z punktu 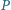 poprowadzono prostą przecinającą dany okrąg
poprowadzono prostą przecinającą dany okrąg 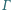 w punktach
w punktach 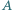 i
i 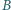 oraz prostą styczną do
oraz prostą styczną do 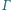 w punkcie
w punkcie 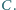 Wykaż, że
Wykaż, że 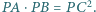
Okrąg 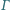 jest styczny do prostej
jest styczny do prostej 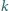 w punkcie
w punkcie 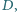 cięciwa
cięciwa 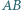 tego okręgu jest równoległa do
tego okręgu jest równoległa do 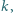 punkt
punkt 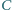 należy do prostej
należy do prostej 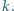 Proste
Proste 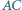 i
i 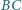 przecinają okrąg
przecinają okrąg 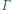 w drugich punktach
w drugich punktach 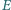 i
i 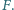 Wykaż, że prosta
Wykaż, że prosta 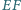 przechodzi przez środek odcinka
przechodzi przez środek odcinka 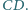
W sytuacji z zadania 4 wykaż, że proste 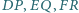 przecinają się w jednym punkcie
przecinają się w jednym punkcie 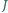 oraz że punkty
oraz że punkty 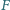 i
i 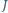 są symetryczne względem prostej
są symetryczne względem prostej 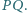
Przez dany punkt leżący we wnętrzu kąta poprowadzić prostą o najkrótszym odcinku między jego ramionami.
Przez dany punkt 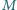 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 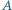 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 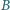 i
i 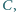 wyznacza trójkąt
wyznacza trójkąt 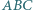 o najmniejszym polu.
o najmniejszym polu.
Wykazać, że maksymalne pole trójkąta zawartego w kwadracie jednostkowym jest równe 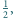 a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.
a minimalne pole trójkąta zawierającego kwadrat jednostkowy jest równe 2.
Przez dany punkt 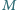 leżący we wnętrzu kąta o wierzchołku
leżący we wnętrzu kąta o wierzchołku 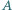 poprowadzić prostą, która, przecinając ramiona kąta w punktach
poprowadzić prostą, która, przecinając ramiona kąta w punktach 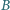 i
i 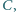 wyznacza trójkąt
wyznacza trójkąt 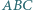 o najmniejszym obwodzie.
o najmniejszym obwodzie.
Czy istnieje co najmniej 5-elementowy zbiór okręgów na płaszczyźnie, taki, że każde trzy okręgi ze zbioru mają punkt wspólny, ale nie istnieje punkt wspólny wszystkich okręgów ze zbioru?
Czy istnieje przekrój dwudziestościanu foremnego płaszczyzną przechodzącą przez jego środek, będący jedenastokątem?
Każda spośród  osób zna dokładnie jedną wiadomość i każda z tych
osób zna dokładnie jedną wiadomość i każda z tych 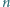 wiadomości jest inna. Co jakiś czas pewna osoba dzwoni do innej i przekazuje jej wszystko, co wie (nie poznając żadnej informacji w zamian). Ile co najmniej rozmów telefonicznych musi się odbyć, zanim wszystkie osoby będą znać wszystkie informacje?
wiadomości jest inna. Co jakiś czas pewna osoba dzwoni do innej i przekazuje jej wszystko, co wie (nie poznając żadnej informacji w zamian). Ile co najmniej rozmów telefonicznych musi się odbyć, zanim wszystkie osoby będą znać wszystkie informacje?
Udowodnić, że dla liczby całkowitej dodatniej 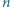 oraz liczb rzeczywistych
oraz liczb rzeczywistych  spełniających
spełniających 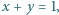 prawdziwa jest tożsamość
prawdziwa jest tożsamość
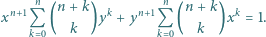
Na płaszczyźnie dany jest zbiór punktów 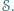 Mówimy, że punkt
Mówimy, że punkt 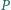 jest widoczny z punktu
jest widoczny z punktu 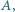 jeśli odcinek
jeśli odcinek 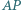 jest zawarty w
jest zawarty w 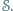 Zbiór
Zbiór 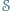 jest widoczny z punktu
jest widoczny z punktu 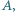 jeśli każdy jego punkt jest widoczny z
jeśli każdy jego punkt jest widoczny z 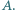
Wykazać, że zbiór 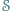 jest widoczny z każdego punktu trójkąta
jest widoczny z każdego punktu trójkąta 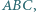 jeśli jest widoczny z każdego wierzchołka tego trójkąta.
jeśli jest widoczny z każdego wierzchołka tego trójkąta.
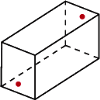
Rys. 1a
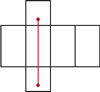
Rys. 1a
Proszę ocenić poprawność poniższego stwierdzenia.
Pokój ma kształt prostopadłościanu o wymiarach 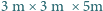 (Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości
(Rys. 1a). Nad środkiem jednej z krótszych krawędzi podłogi, na wysokości 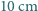 , siedzi pająk. Chce on dotrzeć do punktu położonego
, siedzi pająk. Chce on dotrzeć do punktu położonego 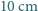 pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.
pod przeciwległą krawędzią sufitu. Najkrótszą drogę, o długości 8 m, oznaczono kolorowym odcinkiem na siatce przedstawionej na rysunku 1b.