Zadania z matematyki - IX 2020»Zadanie 1650
o zadaniu...
- Zadanie pochodzi z artykułu Zadania z matematyki - IX 2020
- Publikacja w Delcie: wrzesień 2020
- Publikacja elektroniczna: 31 sierpnia 2020
Na tablicy zapisanych jest 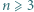 różnych liczb rzeczywistych, przy czym
różnych liczb rzeczywistych, przy czym  jest liczbą nieparzystą. Dla każdej pary
jest liczbą nieparzystą. Dla każdej pary 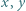 liczb z tablicy na osobnej karteczce zapisano liczbę
liczb z tablicy na osobnej karteczce zapisano liczbę 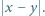 Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.
Wykazać, że wszystkie karteczki można podzielić na dwa stosy o równych sumach zapisanych liczb.

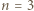 niech
niech 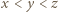 będą elementami zbioru
będą elementami zbioru 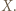 Wówczas na jednym stosie kładziemy karteczkę z liczbą
Wówczas na jednym stosie kładziemy karteczkę z liczbą 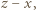 a na drugim - karteczki z liczbami
a na drugim - karteczki z liczbami 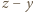 oraz
oraz 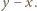
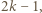 i rozważmy dowolny zbiór
i rozważmy dowolny zbiór 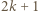 liczb
liczb 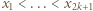 oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb
oraz związane z nimi karteczki. Z założenia indukcyjnego wszystkie karteczki pochodzące wyłącznie od liczb 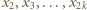 można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące
można podzielić na stosy o równych sumach. Pozostałe karteczki najpierw podzielmy na następujące 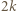 grup:
grup: 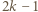 grup po dwie karteczki, z liczbami
grup po dwie karteczki, z liczbami 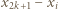 oraz
oraz 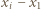 dla
dla 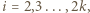 oraz jedna grupa składająca się z pozostałej karteczki z liczbą
oraz jedna grupa składająca się z pozostałej karteczki z liczbą 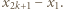 Zauważmy, że w każdej grupie suma liczb z karteczek jest równa
Zauważmy, że w każdej grupie suma liczb z karteczek jest równa 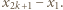 Wobec tego wystarczy karteczki z dowolnych
Wobec tego wystarczy karteczki z dowolnych 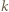 grup dołączyć do jednego stosu, a karteczki z pozostałych
grup dołączyć do jednego stosu, a karteczki z pozostałych 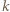 grup - do drugiego stosu. To kończy dowód indukcyjny.
grup - do drugiego stosu. To kończy dowód indukcyjny.