Zadanie ZM-1308
o zadaniu...
- Publikacja w Delcie: marzec 2011
- Publikacja elektroniczna: 02-03-2011
Dany jest wielomian
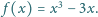 Definiujemy indukcyjnie
Definiujemy indukcyjnie
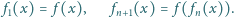
Dowieść, że wielomian
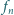 ma
ma
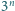 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
Dany jest wielomian
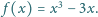 Definiujemy indukcyjnie
Definiujemy indukcyjnie
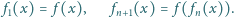
Dowieść, że wielomian
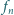 ma
ma
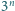 pierwiastków rzeczywistych.
pierwiastków rzeczywistych.
Udowodnić, że spośród dowolnych
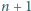 liczb ze zbioru
liczb ze zbioru
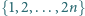 można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
można wybrać dwie, tak żeby jedna była
dzielnikiem drugiej.
Na boku
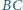 trójkąta
trójkąta
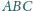 wybrano punkt
wybrano punkt
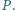 Punkty
Punkty
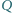 i
i
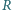 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty
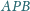 i
i
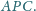 Punkt
Punkt
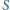 jest punktem styczności okręgu wpisanego w trójkąt
jest punktem styczności okręgu wpisanego w trójkąt
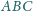 do boku
do boku
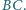 Wykazać, że punkty
Wykazać, że punkty
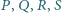 leżą na
jednym okręgu.
leżą na
jednym okręgu.
Sfera wpisana w czworościan
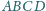 jest styczna do ścian
jest styczna do ścian
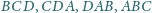 odpowiednio w punktach
odpowiednio w punktach
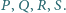 Odcinek
Odcinek
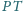 jest średnicą tej sfery, zaś punkty
jest średnicą tej sfery, zaś punkty
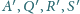 są
punktami przecięcia prostych
są
punktami przecięcia prostych
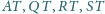 z płaszczyzną
z płaszczyzną
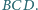 Dowieść , że punkt
Dowieść , że punkt
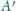 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
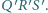
Dowieść, że suma odległości dowolnego punktu leżącego wewnątrz
czworościanu foremnego o krawędzi
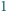 od jego wierzchołków jest
nie większa niż
od jego wierzchołków jest
nie większa niż
Dowieść, że suma odległości dowolnego punktu
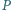 leżącego
wewnątrz trójkąta równobocznego
leżącego
wewnątrz trójkąta równobocznego
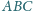 o boku
o boku
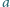 od jego
wierzchołków jest nie większa niż
od jego
wierzchołków jest nie większa niż
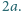
Okrąg wpisany w trójkąt
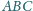 jest styczny do boków
jest styczny do boków
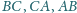 odpowiednio w punktach
odpowiednio w punktach
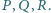 Odcinek
Odcinek
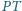 jest średnicą tego
okręgu. Proste
jest średnicą tego
okręgu. Proste
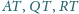 przecinają prostą
przecinają prostą
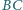 odpowiednio
w punktach
odpowiednio
w punktach
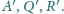 Wykazać, że
Wykazać, że
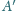 jest środkiem odcinka
jest środkiem odcinka
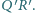
Punkty
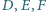 należą odpowiednio do boków
należą odpowiednio do boków
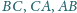 trójkąta
trójkąta
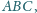 proste
proste
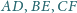 przecinają się w punkcie
przecinają się w punkcie
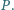 Wykaż, że
Wykaż, że

W trójkącie
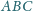 punkty
punkty
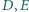 są spodkami dwusiecznych
odpowiednio
są spodkami dwusiecznych
odpowiednio
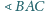 i
i
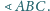 Punkt
Punkt
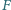 jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
jest spodkiem
dwusiecznej kąta zewnętrznego przy wierzchołku
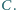 Udowodnij, że
punkty
Udowodnij, że
punkty
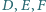 leżą na jednej prostej.
leżą na jednej prostej.
Sfera
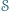 jest styczna do krawędzi
jest styczna do krawędzi
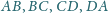 czworościanu
czworościanu
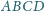 dpowiednio w punktach
dpowiednio w punktach
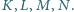 Wykaż, że leżą one
na jednej płaszczyźnie.
Wykaż, że leżą one
na jednej płaszczyźnie.
Punkty
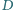 i
i
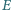 leżą odpowiednio na bokach
leżą odpowiednio na bokach
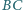 i
i
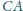 trójkąta
trójkąta
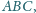 a punkt
a punkt
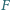 na przedłużeniu boku
na przedłużeniu boku
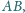 przy czym punkty
przy czym punkty
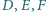 są współliniowe. Punkty
są współliniowe. Punkty
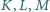 są odpowiednio środkami boków
są odpowiednio środkami boków
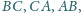 zaś punkty
zaś punkty
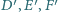 – obrazami symetrycznymi punktów
– obrazami symetrycznymi punktów
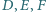 w symetriach względem
w symetriach względem
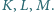 Wykaż, że punkty
Wykaż, że punkty
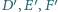 są
współliniowe.
są
współliniowe.
Udowodnij twierdzenie
Twierdzenie (Cevy). Punkty
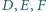 należą odpowiednio do boków
należą odpowiednio do boków
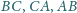 trójkąta
trójkąta
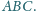 Wówczas proste
Wówczas proste
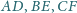 przecinają się w jednym punkcie wtedy
i tylko wtedy, gdy
przecinają się w jednym punkcie wtedy
i tylko wtedy, gdy

Wykaż, że złożenie jednokładności o środku
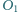 i skali
i skali
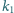 z jednokładnością o środku
z jednokładnością o środku
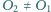 i skali
i skali
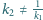 jest
jednokładnością o środku na prostej
jest
jednokładnością o środku na prostej
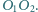
Zadanie 618 zaproponował pan Michał Kieza z Warszawy.
Punkt
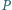 leży wewnątrz równoległoboku
leży wewnątrz równoległoboku
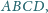 przy czym
środek odcinka
przy czym
środek odcinka
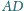 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
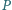 i
i
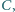 a środek odcinka
a środek odcinka
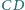 jest jednakowo odległy od punktów
jest jednakowo odległy od punktów
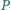 i
i
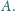 Punkt
Punkt
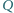 jest środkiem odcinka
jest środkiem odcinka
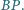 Wykazać, że
Wykazać, że
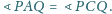
Znaleźć wszystkie funkcje
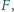 określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
określone na zbiorze wszystkich
liczb całkowitych dodatnich, o wartościach rzeczywistych, spełniające
równanie
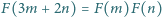 dla każdej pary liczb
całkowitych
dla każdej pary liczb
całkowitych
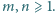
Punkt
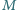 jest środkiem boku
jest środkiem boku
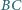 trójkąta ostrokątnego
trójkąta ostrokątnego
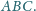 Punkt
Punkt
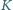 leży na boku
leży na boku
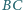 i spełnia warunek
i spełnia warunek
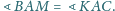 Na odcinku
Na odcinku
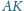 wybrano taki punkt
wybrano taki punkt
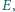 że
że
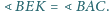 Dowieść, że
Dowieść, że
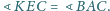
Wewnątrz trójkąta równobocznego
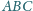 obrano punkt
obrano punkt
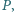 taki że
taki że
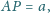

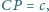 gdzie
gdzie
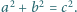 Wyznaczyć długość boku trójkąta
Wyznaczyć długość boku trójkąta
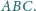
Na płaszczyźnie dane są dwa trójkąty równoboczne
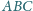 i
i
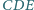 (mające wspólny wierzchołek
(mające wspólny wierzchołek
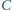 ) oraz punkty
) oraz punkty
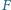 i
i
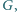 takie
że
takie
że
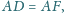
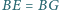 i
i
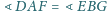 (jako kąty
skierowane). Wykazać, że trójkąt
(jako kąty
skierowane). Wykazać, że trójkąt
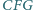 jest równoboczny.
jest równoboczny.
Dany jest trójkąt ostrokątny
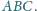 Rozważamy wszystkie takie
trójkąty równoboczne
Rozważamy wszystkie takie
trójkąty równoboczne
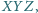 że punkty
że punkty
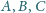 są punktami
wewnętrznymi odcinków
są punktami
wewnętrznymi odcinków
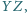
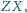
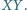 Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
Dowieść, że
środki ciężkości wszystkich rozważanych trójkątów leżą na jednym
okręgu.
Boki
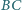 i
i
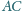 trójkąta
trójkąta
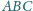 są jednocześnie bokami
kwadratów
są jednocześnie bokami
kwadratów
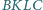 i
i
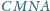 (leżących na zewnątrz trójkąta
(leżących na zewnątrz trójkąta
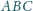 ). Punkty
). Punkty
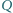 i
i
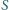 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków
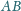 i
i
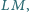 a
a
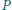 i
i
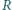 środkami kwadratów
środkami kwadratów
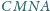 i
i
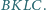 Wykazać, że czworokąt
Wykazać, że czworokąt
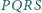 jest
kwadratem.
jest
kwadratem.
Punkty
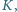
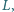
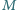 są środkami kwadratów zbudowanych
zewnętrznie na bokach
są środkami kwadratów zbudowanych
zewnętrznie na bokach
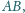
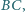
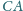 trójkąta
trójkąta
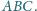 Wykazać, że
Wykazać, że
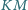 i
i
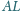 są prostopadłe,
są prostopadłe,
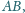
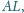
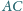 i
i
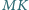 są
wierzchołkami kwadratu.
są
wierzchołkami kwadratu.Losujemy jedną rodzinę spośród rodzin z dwojgiem dzieci. Wiemy, że w rodzinie jest chłopiec, który ma na imię Antoni. Jaka jest szansa, że w rodzinie jest dwóch chłopców.
Losujemy jedną rodzinę spośród rodzin z dwojgiem dzieci. Jaka jest szansa, że wybierzemy rodzinę z dwoma chłopcami, jeśli wiemy, że w tej rodzinie jest co najmniej jeden chłopiec?
Dane są liczby całkowite dodatnie
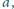
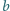 o następującej własności:
o następującej własności:
dla każdej liczby całkowitej dodatniej
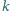 liczby
liczby
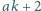 oraz
oraz
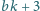 nie są względnie pierwsze. Udowodnić, że
nie są względnie pierwsze. Udowodnić, że
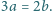
Rozstrzygnąć, czy kwadrat o wymiarach
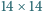 można rozciąć na
prostokąty o wymiarach
można rozciąć na
prostokąty o wymiarach
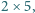
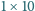 oraz
oraz
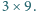
Znaleźć wszystkie liczby rzeczywiste
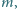 dla których nierówność
dla których nierówność
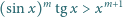
jest spełniona dla
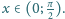
Na wolnych polach kwadratowej planszy o rozmiarach
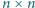 dwaj gracze
na przemian stawiają pionki (nierozróżnialne). Wygrywa gracz, po którego
ruchu znajdą się cztery pionki na dowolnych czterech polach, będących
narożnikami prostokąta o bokach równoległych do krawędzi planszy.
Rozstrzygnąć (w zależności od
dwaj gracze
na przemian stawiają pionki (nierozróżnialne). Wygrywa gracz, po którego
ruchu znajdą się cztery pionki na dowolnych czterech polach, będących
narożnikami prostokąta o bokach równoległych do krawędzi planszy.
Rozstrzygnąć (w zależności od
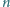 ), który z graczy ma strategię
zwycięską – rozpoczynający czy jego przeciwnik.
), który z graczy ma strategię
zwycięską – rozpoczynający czy jego przeciwnik.
Znaleźć wszystkie funkcje określone na zbiorze liczb rzeczywistych dodatnich, o wartościach w tym samym zbiorze, spełniające nierówność