Zadanie ZM-1491
o zadaniu...
- Publikacja w Delcie: kwiecień 2016
- Publikacja elektroniczna: 30 marca 2016
Sześciokąt 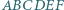 jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że
jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że 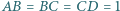 oraz
oraz 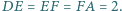
Sześciokąt 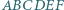 jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że
jest wpisany w okrąg. Oblicz promień tego okręgu, wiedząc, że 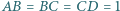 oraz
oraz 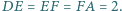
Udowodnić, że istnieje 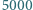 liczb
liczb 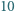 -cyfrowych podzielnych przez
-cyfrowych podzielnych przez 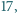 takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
takich że każdą z nich można otrzymać z dowolnej z pozostałych poprzez zmianę kolejności cyfr.
Znaleźć liczbę wielokrotności 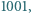 które można zapisać w postaci
które można zapisać w postaci 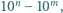 gdzie
gdzie  oraz
oraz 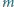 są liczbami całkowitymi spełniającymi
są liczbami całkowitymi spełniającymi 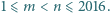
Zadanie 720 (inspirowane zadaniami 194 i 702) zaproponował pan Jerzy Cisło z Wrocławia.
Dla ustalonej liczby naturalnej 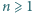 znaleźć najmniejszą liczbę rzeczywistą
znaleźć najmniejszą liczbę rzeczywistą  taką, że dla każdej liczby rzeczywistej
taką, że dla każdej liczby rzeczywistej 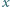 spełniona jest nierówność
spełniona jest nierówność
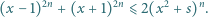
Czternaścioro ludzi prezentowało swoje umiejętności w serii występów; w pojedynczym występie mogła uczestniczyć dowolna liczba osób. Było to siedem par małżeńskich - ale małżonkowie nigdy nie wystąpili razem. Za to każda inna para osób (dowolnej płci) uczestniczyła jednocześnie w dokładnie jednym występie. Wiadomo ponadto, że pewna osoba uczestniczyła w dokładnie dwóch występach. Jaka jest minimalna liczba występów, przy której te warunki mogły być spełnione?
Dany jest czworokąt wypukły 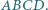 Proste zawierające dwusieczne kątów wewnętrznych
Proste zawierające dwusieczne kątów wewnętrznych 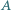 i
i 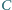 przecinają się w punkcie
przecinają się w punkcie 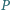 leżącym wewnątrz czworokąta
leżącym wewnątrz czworokąta 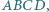 a proste zawierające dwusieczne kątów wewnętrznych
a proste zawierające dwusieczne kątów wewnętrznych 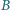 i
i 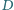 przecinają się w punkcie
przecinają się w punkcie 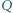 na zewnątrz czworokąta. Udowodnij, że jeżeli kąt
na zewnątrz czworokąta. Udowodnij, że jeżeli kąt 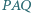 jest prosty, to również kąt
jest prosty, to również kąt 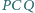 jest prosty.
jest prosty.
Odcinek 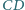 jest średnicą okręgu
jest średnicą okręgu 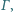 a cięciwa
a cięciwa 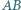 jest prostopadła do tej średnicy. Punkt
jest prostopadła do tej średnicy. Punkt 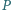 należy do krótszego łuku
należy do krótszego łuku 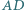 okręgu
okręgu 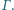 Proste
Proste 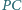 i
i 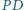 przecinają prostą
przecinają prostą 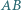 odpowiednio w punktach
odpowiednio w punktach 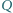 i
i 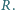 Wykaż, że
Wykaż, że 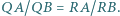
Dany jest trójkąt 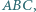 w którym kąt przy wierzchołku
w którym kąt przy wierzchołku 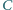 jest prosty. Punkt
jest prosty. Punkt 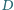 jest spodkiem wysokości opuszczonej z wierzchołka
jest spodkiem wysokości opuszczonej z wierzchołka 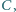 a okrąg wpisany w dany trójkąt jest styczny do boków
a okrąg wpisany w dany trójkąt jest styczny do boków 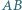 i
i 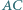 odpowiednio w punktach
odpowiednio w punktach 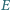 i
i 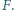 Wykaż, że ortocentrum trójkąta
Wykaż, że ortocentrum trójkąta 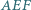 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 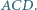
Udowodnij, że środek okręgu wpisanego w trójkąt jest ortocentrum trójkąta utworzonego przez środki okręgów dopisanych.
Wyznacz środek ciężkości obwodu trójkąta (czyli trójkątnej drucianej ramki).
W trójkącie 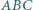 punkty
punkty 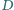 i
i 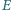 są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach
są spodkami dwusiecznych kątów wewnętrznych przy wierzchołkach 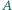 i
i 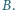 Punkt
Punkt 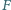 jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku
jest spodkiem dwusiecznej zewnętrznej kąta przy wierzchołku 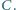 Wykaż, że punkty
Wykaż, że punkty 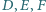 są współliniowe.
są współliniowe.
Rozstrzygnąć, czy istnieją liczby naturalne 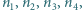 wszystkie większe od
wszystkie większe od 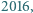 spełniające równanie
spełniające równanie

W trójkąt 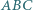 wpisany jest okrąg o promieniu
wpisany jest okrąg o promieniu 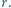 Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa
Proste styczne do okręgu i równoległe do boków trójkąta odcinają od niego trzy trójkąty. Wykaż, że suma promieni okręgów wpisanych w te trzy trójkąty jest równa 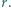
Dane są takie liczby całkowite dodatnie 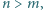 że liczby
że liczby 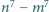 oraz
oraz 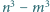 są względnie pierwsze. Wykaż, że liczby
są względnie pierwsze. Wykaż, że liczby 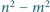 i
i 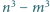 są również względnie pierwsze.
są również względnie pierwsze.
Zadanie 718 zaproponował pan Tomasz Ordowski.
Dowieść, że dla dowolnych dodatnich liczb całkowitych 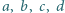 zachodzi równość
zachodzi równość
![[a, b,c,d] =-a⋅b-⋅c⋅d- ⋅--(a,-b,c)⋅(a,b,d)-⋅(a,c,d)-⋅(b,c,d)---. (a, b,c,d) (a,b) ⋅(a,c)⋅(a,d) ⋅(b,c) ⋅(b,d) ⋅(c,d)](/math/temat/matematyka/teoria_liczb/zadania/2016/02/29/zm-k44-718/2x-f64cd4667e200cae0b647d7a1c3170835ae3432d-dm-2C,6B,73-FF,FF,FF.gif)
Nawias kwadratowy oznacza najmniejszą wspólną wielokrotność, zaś nawias okrągły - największy wspólny dzielnik liczb ujętych w ów nawias.
Dany jest trójkąt 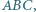 w którym
w którym 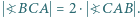 Odcinek
Odcinek 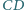 (o końcu
(o końcu 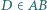 ) jest dwusieczną kąta
) jest dwusieczną kąta 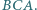 Punkt
Punkt 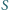 jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach
jest środkiem okręgu, stycznego zewnętrznie do okręgów opisanych na trójkątach 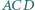 i
i 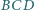 oraz stycznego do półprostej
oraz stycznego do półprostej 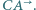 Udowodnić, że proste
Udowodnić, że proste 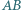 i
i 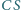 są prostopadłe.
są prostopadłe.
Czy istnieje wielościan o 333 ścianach, z których każda jest trójkątem?
Czy istnieje wielościan o 7 krawędziach?
Czy istnieje wielościan wypukły mający 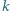 krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca
krawędzi oraz płaszczyzna nie przechodząca przez żaden z jego wierzchołków i przecinająca  krawędzi, przy czym
krawędzi, przy czym 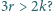
Czy istnieje wielościan wypukły, w którym 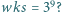
Udowodnij, że w każdym wielościanie wypukłym 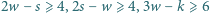 oraz
oraz 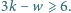
Zadanie 6 pochodzi z Ligi Zadaniowej Olimpiady Matematycznej Gimnazjalistów.
Pewien wielościan wypukły ma 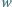 wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
wierzchołków. Oblicz sumę kątów płaskich wszystkich jego ścian.
Udowodnij, że każdy wielościan wypukły ma ścianę trójkątną lub naroże trójścienne.
Wykaż, że w każdym wielościanie wypukłym suma liczby ścian trójkątnych i liczby naroży trójściennych jest większa lub równa 8.
Krawiec ma worek płaskich pięciokątów foremnych o boku 1 oraz worek płaskich sześciokątów foremnych o boku 1. Jakie wielościany wypukłe może z nich uszyć?
Jakie istnieją wielościany foremne wypukłe?
Czy istnieje wielościan wypukły o czworokątnych ścianach i o 25 krawędziach?
Wykaż, że każdy wielościan wypukły ma wierzchołek o mniej niż 6 krawędziach oraz ścianę o mniej niż 6 bokach.
Dowieść, że jeżeli 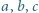 są długościami boków trójkąta, to
są długościami boków trójkąta, to

Czy współczynnik 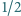 (po prawej stronie) może być zastąpiony przez liczbę większą?
(po prawej stronie) może być zastąpiony przez liczbę większą?
Dane są dwie różne liczby całkowite dodatnie 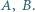 Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o
Wykazać, że zbiór wszystkich liczb całkowitych nieujemnych może być przedstawiony jako suma rozłącznych zbiorów trójelementowych, przy czym w każdym z tych zbiorów liczba środkowa (co do wielkości) różni się od jednej z dwóch pozostałych liczb o 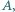 zaś od drugiej o
zaś od drugiej o