Zadanie ZM-1321
o zadaniu...
- Publikacja w Delcie: sierpień 2011
- Publikacja elektroniczna: 31-07-2011
Dane są: jeden klocek
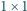 i dwadzieścia jeden klocków
i dwadzieścia jeden klocków
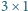 .
Udowodnić, że tymi klockami można pokryć szachownicę
.
Udowodnić, że tymi klockami można pokryć szachownicę
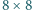 (klocki
(klocki
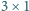 można kłaść poziomo lub pionowo) wtedy i tylko
wtedy, gdy klocek
można kłaść poziomo lub pionowo) wtedy i tylko
wtedy, gdy klocek
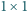 położony jest na jednym z pól c3, f3, c6
lub f6.
położony jest na jednym z pól c3, f3, c6
lub f6.

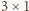 przykrywa dokładnie jedno zamalowane pole. Tych
klocków jest 21, więc klocek
przykrywa dokładnie jedno zamalowane pole. Tych
klocków jest 21, więc klocek
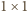 musi leżeć na zamalowanym
polu. Wykonujemy symetryczne kolorowanie, ale innym kolorem niż
poprzednio, względem prostej zawierającej wspólny bok pól a4 i a5.
Widać już, że klocek
musi leżeć na zamalowanym
polu. Wykonujemy symetryczne kolorowanie, ale innym kolorem niż
poprzednio, względem prostej zawierającej wspólny bok pól a4 i a5.
Widać już, że klocek
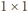 musi leżeć na jednym z czterech pól
zamalowanych obydwoma kolorami, a to właśnie pola wymienione
w tezie zadania. Z drugiej strony łatwo sprawdzić, że jeśli leży on
na jednym z tych pól, to można skonstruować odpowiednie pokrycie
szachownicy.
musi leżeć na jednym z czterech pól
zamalowanych obydwoma kolorami, a to właśnie pola wymienione
w tezie zadania. Z drugiej strony łatwo sprawdzić, że jeśli leży on
na jednym z tych pól, to można skonstruować odpowiednie pokrycie
szachownicy.
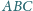 jest styczny do boków
jest styczny do boków
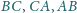 odpowiednio w punktach
odpowiednio w punktach
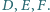 Prowadzimy trzy
proste: przez środki odcinków
Prowadzimy trzy
proste: przez środki odcinków
 i
i
 przez środki
odcinków
przez środki
odcinków
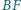 i
i
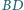 oraz przez środki odcinków
oraz przez środki odcinków
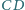 i
i
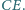 Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
Wykazać, że środek okręgu opisanego na trójkącie wyznaczonym
przez te trzy proste pokrywa się ze środkiem okręgu opisanego na trójkącie
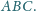
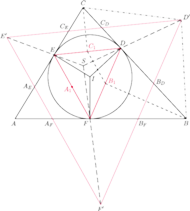
 będą środkami odcinków
będą środkami odcinków
 Z twierdzenia Talesa wynika, że
Z twierdzenia Talesa wynika, że

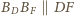 i
i
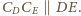 Przez
Przez
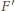 oznaczamy punkt wspólny prostych
oznaczamy punkt wspólny prostych
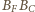 i
i
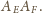 Analogicznie definiujemy punkty
Analogicznie definiujemy punkty
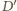 i
i
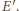 Boki
trójkątów
Boki
trójkątów
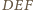 i
i
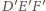 są odpowiednio równoległe, więc
punkt
są odpowiednio równoległe, więc
punkt
 w którym przecinają się proste
w którym przecinają się proste
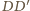 i
i
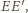 jest
środkiem jednokładności w skali
jest
środkiem jednokładności w skali
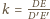 przekształcającej trójkąt
przekształcającej trójkąt
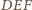 na trójkąt
na trójkąt
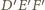 (
(
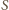 leży też na prostej
leży też na prostej
 ).
).
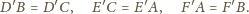
 w skali
w skali
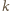 przekształca okrąg
przekształca okrąg
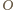 opisany na trójkącie
opisany na trójkącie
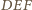 na okrąg
na okrąg
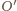 opisany na trójkącie
opisany na trójkącie
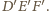 Środek okręgu
Środek okręgu
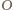 leży na prostopadłych do prostych
leży na prostopadłych do prostych
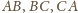 przechodzących
przez wierzchołki
przechodzących
przez wierzchołki
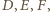 więc środek okręgu
więc środek okręgu
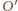 leży na
prostopadłych do prostych
leży na
prostopadłych do prostych
 przechodzących przez wierzchołki
przechodzących przez wierzchołki
 Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
Na mocy lematu (dowód w artykule) te prostopadłe są
symetralnymi boków trójkąta
 więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
więc ich punkt wspólny to
środek okręgu opisanego na trójkącie
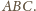
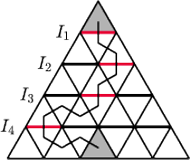
 podzielono na
jednostkowe trójkąty równoboczne, analogicznie do rysunku 2. Ile jest
ścieżek prowadzących od trójkąta w górnym rzędzie do środkowego
trójkąta w dolnym rzędzie, takich że kolejne trójkąty na ścieżce mają
wspólny bok, a ścieżka nigdy nie wraca do góry (z rzędu niższego do
wyższego) ani nie przechodzi dwa razy przez żaden trójkąt?
podzielono na
jednostkowe trójkąty równoboczne, analogicznie do rysunku 2. Ile jest
ścieżek prowadzących od trójkąta w górnym rzędzie do środkowego
trójkąta w dolnym rzędzie, takich że kolejne trójkąty na ścieżce mają
wspólny bok, a ścieżka nigdy nie wraca do góry (z rzędu niższego do
wyższego) ani nie przechodzi dwa razy przez żaden trójkąt?
 na jeden sposób,
na jeden sposób,
 na
2 sposoby,
na
2 sposoby,
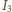 na 3 itd., wreszcie
na 3 itd., wreszcie
 na 2010 sposobów. Zatem
ścieżek jest co najwyżej
na 2010 sposobów. Zatem
ścieżek jest co najwyżej
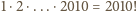 – nietrudno
zobaczyć, że jest ich dokładnie tyle, gdyż każdy wybór jednego z
– nietrudno
zobaczyć, że jest ich dokładnie tyle, gdyż każdy wybór jednego z
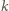 pododcinków odcinka
pododcinków odcinka
 który ma przeciąć ścieżka,
definiuje poprawną ścieżkę.
który ma przeciąć ścieżka,
definiuje poprawną ścieżkę.
 o kącie prostym przy
wierzchołku
o kącie prostym przy
wierzchołku
 i boku
i boku
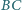 długości
długości
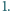 Punkty
Punkty
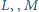 i
i
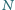 to odpowiednio środki boków
to odpowiednio środki boków
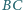 ,
,
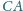 i
i
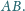 . Wiedząc, że proste
. Wiedząc, że proste
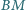 i
i
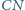 są prostopadłe,
obliczyć długość odcinka
są prostopadłe,
obliczyć długość odcinka
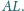

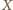 środek ciężkości trójkąta
środek ciężkości trójkąta
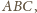 czyli
punkt przecięcia odcinków
czyli
punkt przecięcia odcinków
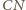 i
i
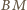 . Zauważmy, że
. Zauważmy, że
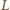 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie
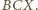 Zatem
Zatem
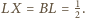 Ponieważ
Ponieważ
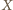 jest środkiem ciężkości, więc
jest środkiem ciężkości, więc
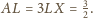
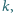 że liczba
że liczba
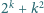 jest
pierwsza.
jest
pierwsza.
 jest pierwsza. Jest ona większa od 2, więc
nieparzysta. Zatem liczba
jest pierwsza. Jest ona większa od 2, więc
nieparzysta. Zatem liczba
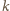 musi być nieparzysta. Ale wówczas
musi być nieparzysta. Ale wówczas
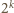 daje resztę
daje resztę
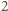 z dzielenia przez
z dzielenia przez
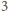 . Skoro kwadrat liczby
całkowitej daje resztę
. Skoro kwadrat liczby
całkowitej daje resztę
 lub
lub
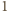 przy dzieleniu przez
przy dzieleniu przez
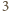 , to aby
, to aby
 nie było podzielne przez
nie było podzielne przez
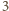 , potrzeba, aby
, potrzeba, aby
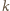 było
podzielne przez
było
podzielne przez
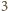 . Ponieważ
. Ponieważ
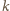 jest liczbą pierwszą, jedyna
możliwość to
jest liczbą pierwszą, jedyna
możliwość to
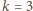 i wówczas
i wówczas
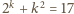 jest liczbą
pierwszą.
jest liczbą
pierwszą.
 znajdują się punkty
znajdują się punkty
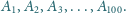 Udowodnij, że na brzegu tego koła istnieje taki
punkt
Udowodnij, że na brzegu tego koła istnieje taki
punkt
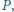 dla którego
dla którego

 i
i
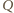 będą końcami dowolnej średnicy rozważanego
koła. Wtedy dla dowolnego punktu
będą końcami dowolnej średnicy rozważanego
koła. Wtedy dla dowolnego punktu
 płaszczyzny mamy
płaszczyzny mamy
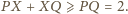 Nierówność ta jest tzw. nierównością
trójkąta dla trójki punktów
Nierówność ta jest tzw. nierównością
trójkąta dla trójki punktów
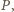
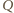 i
i
 Więc dla
Więc dla
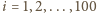 otrzymujemy
otrzymujemy
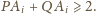
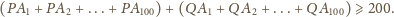
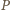 lub
lub
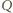 spełnia warunki zadania.
spełnia warunki zadania.
 będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
będzie liczbą naturalną większą od 1. Dla jakich dodatnich liczb
rzeczywistych
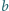 można znaleźć funkcję
można znaleźć funkcję
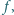 ciągłą na przedziale
ciągłą na przedziale
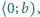 różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:
różniczkowalną wewnątrz tego przedziału oraz spełniającą
warunki:

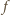 będzie funkcją, spełniającą podane warunki. Zauważmy, że
będzie funkcją, spełniającą podane warunki. Zauważmy, że
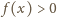 w przedziale
w przedziale
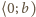 (w przeciwnym razie, oznaczając przez
(w przeciwnym razie, oznaczając przez
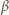 najmniejsze miejsce zerowe funkcji
najmniejsze miejsce zerowe funkcji
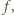 mielibyśmy w przedziale
mielibyśmy w przedziale
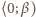 nierówności
nierówności

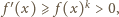 skąd
skąd
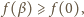 czyli
czyli
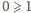 ).
).
 z pochodną
z pochodną
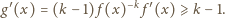
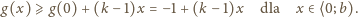
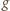 w przedziale
w przedziale
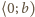 są ujemne. Tak więc
są ujemne. Tak więc
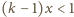 dla wszystkich
dla wszystkich
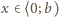 ; to znaczy, że liczba
; to znaczy, że liczba
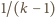 nie należy do tego przedziału – czyli zachodzi nierówność
nie należy do tego przedziału – czyli zachodzi nierówność
 Na odwrót, jeżeli
Na odwrót, jeżeli
 to określamy
funkcję
to określamy
funkcję
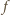 wzorem
wzorem
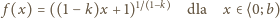
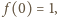
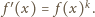 Stąd
odpowiedź: liczby
Stąd
odpowiedź: liczby
 o które pyta zadanie, są scharakteryzowane
nierównością
o które pyta zadanie, są scharakteryzowane
nierównością
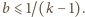
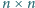 liczby
liczby
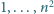 tak, by w każdym wierszu suma liczb była całkowitą
potęgą dwójki?
tak, by w każdym wierszu suma liczb była całkowitą
potęgą dwójki?
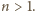 Przypuśćmy, że to się udało i niech
Przypuśćmy, że to się udało i niech
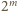 będzie minimalną sumą liczb w wierszu. Jest ona dzielnikiem sumy
liczb w każdym wierszu, więc i sumy liczb we wszystkich wierszach,
równej
będzie minimalną sumą liczb w wierszu. Jest ona dzielnikiem sumy
liczb w każdym wierszu, więc i sumy liczb we wszystkich wierszach,
równej
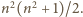 Jasne, że
Jasne, że
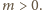 Zatem liczba
Zatem liczba
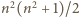 musi być parzysta, co oznacza, że
musi być parzysta, co oznacza, że
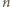 jest
liczbą parzystą. Liczba
jest
liczbą parzystą. Liczba
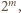 względnie pierwsza z czynnikiem
względnie pierwsza z czynnikiem
 musi dzielić
musi dzielić
 To już daje sprzeczność, bowiem
To już daje sprzeczność, bowiem
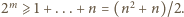
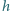 z wierzchołka
z wierzchołka
 na podstawę
na podstawę
 w trójkącie
w trójkącie
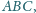 mając dane
mając dane
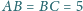 i
i
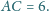
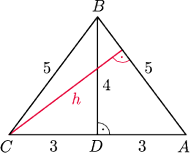
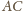 było podstawą, i niech
było podstawą, i niech
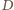 będzie
spodkiem wysokości z wierzchołka
będzie
spodkiem wysokości z wierzchołka
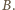 Wtedy
Wtedy
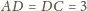 oraz
oraz
 zatem
zatem
 Ponieważ jednocześnie
Ponieważ jednocześnie
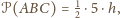 to
to
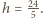
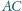 i
i
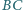 trójkąta równoramiennego
trójkąta równoramiennego
 mają
długość 1. Dla jakiej podstawy
mają
długość 1. Dla jakiej podstawy
 pole tego trójkąta jest
maksymalne?
pole tego trójkąta jest
maksymalne?
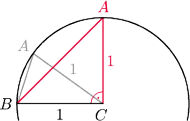
 było podstawą. Wtedy wierzchołek
było podstawą. Wtedy wierzchołek
 leży na okręgu o środku
leży na okręgu o środku
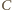 i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
i promieniu 1. Pole trójkąta jest
maksymalne, gdy wysokość z
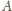 jest maksymalna (bo podstawa
jest maksymalna (bo podstawa
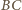 ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
ma ustaloną długość 1), czyli gdy wysokość ta jest równa 1.
Zachodzi to dla
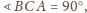 czyli dla
czyli dla
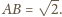
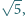
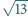 i
i
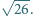
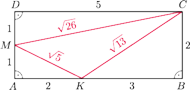
 o bokach
o bokach
 i
i
 Niech
punkt
Niech
punkt
 będzie środkiem boku
będzie środkiem boku
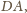 a punkt
a punkt
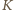 niech należy
do boku
niech należy
do boku
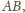 przy czym
przy czym
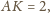
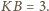 Wtedy z twierdzenia
Pitagorasa
Wtedy z twierdzenia
Pitagorasa
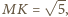
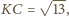
 Należy
obliczyć pole trójkąta
Należy
obliczyć pole trójkąta
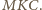 Jest ono równe
Jest ono równe
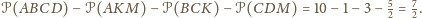
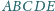 kąty przy wierzchołkach
kąty przy wierzchołkach
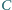 i
i
 są proste. Oblicz
są proste. Oblicz
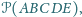 jeśli
jeśli
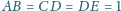 oraz
oraz
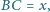
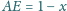 dla
dla
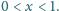
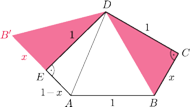
 obok trójkąta
obok trójkąta
 jak na rysunku
(
jak na rysunku
(
 oznacza odpowiednik wierzchołka
oznacza odpowiednik wierzchołka
 ). Wtedy w trójkącie
). Wtedy w trójkącie
 podstawa
podstawa
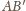 ma długość
ma długość
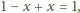 wysokość
wysokość
 jest równa 1, więc pole jest równe
jest równa 1, więc pole jest równe
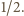 Pozostałą
częścią pięciokąta jest trójkąt
Pozostałą
częścią pięciokąta jest trójkąt
 Przystaje on do trójkąta
Przystaje on do trójkąta
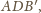 ponieważ
ponieważ

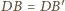 oraz bok
oraz bok
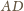 jest wspólny. Stąd
jest wspólny. Stąd
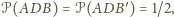 więc pole
pięciokąta równe jest 1.
więc pole
pięciokąta równe jest 1.
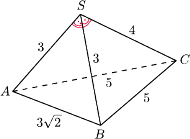
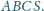 Krawędzie podstawy mają
długości
Krawędzie podstawy mają
długości
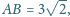
 Krawędzie boczne mają
długości
Krawędzie boczne mają
długości

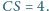 Oblicz objętość tego
ostrosłupa.
Oblicz objętość tego
ostrosłupa.
 jest trójkątem o bokach długości
jest trójkątem o bokach długości
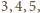 ma zatem
kąt prosty przy wierzchołku
ma zatem
kąt prosty przy wierzchołku
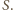 Analogicznie
Analogicznie
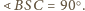 Ściana
Ściana
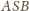 ma boki długości
ma boki długości
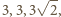 czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
czyli jest połówką kwadratu
o boku 3, więc też ma kąt prosty przy wierzchołku
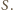 Ustawmy dany
ostrosłup inaczej: niech
Ustawmy dany
ostrosłup inaczej: niech
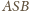 będzie podstawą. Wobec powyższych
obserwacji
będzie podstawą. Wobec powyższych
obserwacji
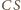 jest wtedy wysokością i
jest wtedy wysokością i
 Stąd
objętość ostrosłupa to
Stąd
objętość ostrosłupa to
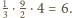

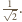 Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
Środki przeciwległych krawędzi
czworościanu są środkami przeciwległych ścian sześcianu, więc ich
odległość równa jest długości krawędzi sześcianu.
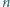 zawodników (
zawodników (
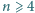 ).
Każdy zawodnik rozegrał dokładnie jeden mecz z każdym innym zawodnikiem,
żaden mecz nie zakończył się remisem. Po turnieju wszyscy zawodnicy usiedli
przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą
siedzącą obok niego z jego lewej strony. Wykaż, że istnieją tacy trzej
zawodnicy
).
Każdy zawodnik rozegrał dokładnie jeden mecz z każdym innym zawodnikiem,
żaden mecz nie zakończył się remisem. Po turnieju wszyscy zawodnicy usiedli
przy okrągłym stole w taki sposób, że każdy zawodnik wygrał z osobą
siedzącą obok niego z jego lewej strony. Wykaż, że istnieją tacy trzej
zawodnicy
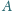 ,
,
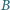 i
i
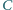 , że
, że
 wygrał z
wygrał z
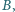
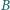 wygrał z
wygrał z
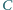 oraz
oraz
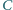 wygrał z
wygrał z
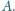

 sprawa jest jasna. Załóżmy więc, że twierdzenie jest
prawdziwe dla pewnego
sprawa jest jasna. Załóżmy więc, że twierdzenie jest
prawdziwe dla pewnego
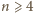 i spróbujmy je udowodnić dla
i spróbujmy je udowodnić dla
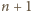 zawodników. Nazwijmy ich
zawodników. Nazwijmy ich
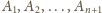 i przyjmijmy, że
w tej właśnie kolejności siedzą przy stole, czyli
i przyjmijmy, że
w tej właśnie kolejności siedzą przy stole, czyli
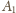 wygrał z
wygrał z
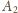 ,
który wygrał z
,
który wygrał z
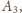 itd.
itd.
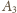 wygrał z
wygrał z
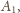 to mamy tezę. W przeciwnym
przypadku tezę otrzymujemy, stosując założenie indukcyjne do zawodników
to mamy tezę. W przeciwnym
przypadku tezę otrzymujemy, stosując założenie indukcyjne do zawodników

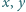 należących do przedziału
należących do przedziału
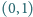 spełniona jest nierówność
spełniona jest nierówność
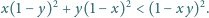
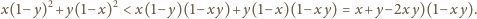
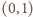 zachodzi nierówność
zachodzi nierówność
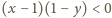 ,
równoważna
,
równoważna
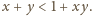 Zatem
Zatem
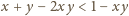 , co
daje tezę.
, co
daje tezę.
 , w którym pola trójkątów
, w którym pola trójkątów
 ,
,
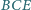 ,
,
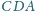 ,
,
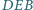 i
i
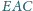 są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
są równe.
Wykaż, że każda przekątna tego pięciokąta jest równoległa do pewnego
jego boku.
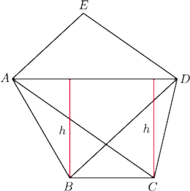
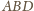 i
i
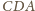 mają równe pola oraz wspólny
bok
mają równe pola oraz wspólny
bok
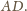 Wobec tego wysokości tych trójkątów poprowadzone do
boku
Wobec tego wysokości tych trójkątów poprowadzone do
boku
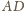 są równe. Ponadto punkty
są równe. Ponadto punkty
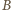 i
i
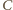 leżą po
tej samej stronie prostej
leżą po
tej samej stronie prostej
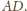 Stąd wniosek, że przekątna
Stąd wniosek, że przekątna
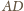 jest
równoległa do boku
jest
równoległa do boku
 Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
Analogicznie dowodzimy, że pozostałe cztery
przekątne pięciokąta
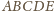 są równoległe do odpowiednich jego
boków
są równoległe do odpowiednich jego
boków
 leży wewnątrz czworościanu
leży wewnątrz czworościanu
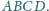 Dowieść,
że
Dowieść,
że

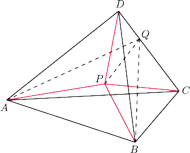
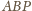 przecina krawędź
przecina krawędź
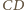 w punkcie
w punkcie
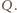 Stosując twierdzenie 1, otrzymujemy
Stosując twierdzenie 1, otrzymujemy
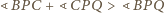
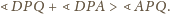
 więc dostajemy
więc dostajemy
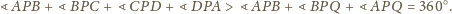
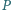 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
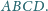 Dowieść, że
Dowieść, że

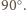 Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
Wtedy z twierdzenia 1 z artykułu wynika, że suma kątów
płaskich w każdym wierzchołku jest większa niż
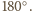 W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
W takim
razie suma wszystkich kątów płaskich w czworościanie jest większa od
 Sprzeczność, gdyż ta suma jest równa
Sprzeczność, gdyż ta suma jest równa

 kąty
kąty

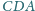 są
rozwarte, a krawędzie
są
rozwarte, a krawędzie
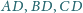 są równe. Dowieść, że trójkąt
są równe. Dowieść, że trójkąt
 jest ostrokątny.
jest ostrokątny.
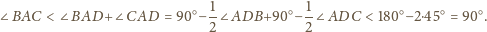
 są ostre.
są ostre.
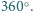
 jest figurą złożoną z odcinków
jest figurą złożoną z odcinków
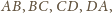 zaś suma jego kątów jest równa sumie kątów
płaskich utworzonych przez każde trzy kolejne jego wierzchołki
zaś suma jego kątów jest równa sumie kątów
płaskich utworzonych przez każde trzy kolejne jego wierzchołki
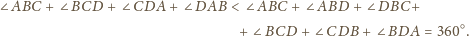
 będzie liczbą krawędzi czworościanu o długości
będzie liczbą krawędzi czworościanu o długości
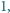 a
a
 liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
liczbą ścian rozwartokątnych. Wyznaczyć największą możliwą
wartość sumy
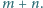
 w którym
w którym
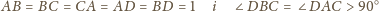
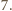 Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
Wykażemy, że więcej się nie
da. Przypuśćmy, że istnieje czworościan, dla którego dana suma jest
większa niż
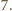 Wynika stąd w szczególności, że liczba krawędzi
długości
Wynika stąd w szczególności, że liczba krawędzi
długości
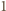 jest równa co najmniej
jest równa co najmniej
 Jeśli jest
Jeśli jest
 krawędzi
długości
krawędzi
długości
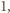 to nie ma kątów rozwartych. Jeśli jest
to nie ma kątów rozwartych. Jeśli jest
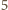 krawędzi
długości
krawędzi
długości
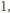 to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
to mogą być co najwyżej dwa kąty rozwarte. Zatem liczba
krawędzi długości
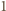 musi być równa
musi być równa
 Tym samym
liczba kątów rozwartych musi być równa
Tym samym
liczba kątów rozwartych musi być równa
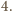 Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:
Zatem żadne
trzy krawędzie nie mogą więc tworzyć trójkąta równobocznego. To
wyzancza nam jedną (z dokładnością do permutacji wierzchołków)
konfigurację:

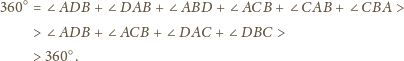
 będzie dowolnym punktem wewnątrz czworościanu
będzie dowolnym punktem wewnątrz czworościanu
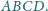 Dowieść, że
Dowieść, że


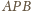 przecina krawędź
przecina krawędź
 w
punkcie
w
punkcie
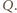 Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy
Wtedy korzystając dwukrotnie z twierdzenia 1 z artykułu
dostajemy

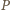 leży wewnątrz trójkąta
leży wewnątrz trójkąta
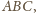 to
to
 –
wystarczy rozważyć sferę o środku
–
wystarczy rozważyć sferę o środku
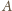 i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
i otrzymujemy sferyczną wersję
tej nierówności. Analogicznie dowodzimy, że
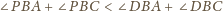
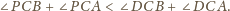

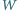 zawarta jest półprosta
zawarta jest półprosta
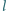 przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
przechodząca
przez jego wierzchołek. Dowieść, że suma kątów utworzonych przez prostą
 z krawędziami kąta
z krawędziami kąta
 nie przekracza sumy kątów płaskich kąta
nie przekracza sumy kątów płaskich kąta
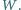
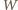 jest wierzchołkiem danego kąta trójściennego,
jest wierzchołkiem danego kąta trójściennego,
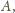
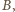
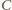 – dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
– dowolnymi punktami leżącymi na różnych
krawędziach tego kąta, zaś
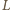 dowolnym punktem na półprostej
dowolnym punktem na półprostej
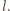 Mamy udowodnić, że
Mamy udowodnić, że
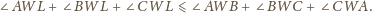
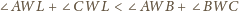
 pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.
pokryje się z jednym z ramion kąta, a ponadto
pozostałe dwa ramiona również się pokryją.
 jest wspólnym wierzchołkiem danych dwóch
kątów oraz przyjmijmy, że pewna płaszczyzna przecinająca wszystkie
ściany obywdu kątów tworzy w przekroju wewnętrznego kąta wielokąt
jest wspólnym wierzchołkiem danych dwóch
kątów oraz przyjmijmy, że pewna płaszczyzna przecinająca wszystkie
ściany obywdu kątów tworzy w przekroju wewnętrznego kąta wielokąt
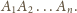 Niech ponadto półprosta
Niech ponadto półprosta
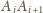 przecina zewnętrzny
kąt w punkcie
przecina zewnętrzny
kąt w punkcie
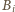 (jak zwykle idneksowanie modulo
(jak zwykle idneksowanie modulo
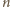 ). Dla
). Dla
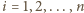 zachodzą nierówności
zachodzą nierówności
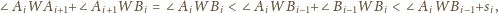
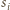 jest sumą kątów płaskich przy wierzchołku
jest sumą kątów płaskich przy wierzchołku
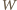 części
kąta zewnętrznego ograniczonej płaszczyznami
części
kąta zewnętrznego ograniczonej płaszczyznami
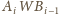 i
i
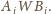 Dodając te wszystkie nierówności stronami dostajemy
tezę.
Dodając te wszystkie nierówności stronami dostajemy
tezę.
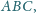 w którym
w którym
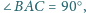 jest podstawą ostrosłupa
jest podstawą ostrosłupa
 Ponadto zachodzą równości
Ponadto zachodzą równości

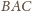 uzupełniamy do prostokąta
uzupełniamy do prostokąta
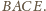 Wówczas z
równości
Wówczas z
równości
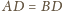 wynika, że
wynika, że
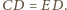 To w połączeniu z
To w połączeniu z
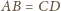 dowodzi, że trójkąt
dowodzi, że trójkąt
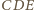 jest równoboczny.
Zatem
jest równoboczny.
Zatem
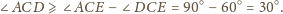

 o kącie prostym
przy wierzchołku
o kącie prostym
przy wierzchołku
 . Znaleźć zbiór takich punktów
. Znaleźć zbiór takich punktów
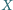 z wnętrza trójkąta
z wnętrza trójkąta
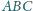 , że jeśli prosta
, że jeśli prosta
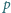 równoległa do
podstawy
równoległa do
podstawy
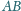 przechodząca przez punkt
przechodząca przez punkt
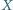 przecina ramiona
przecina ramiona
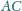 i
i
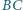 w punktach
w punktach
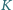 i
i
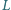 , zaś
, zaś
 jest prostą
prostopadłą do
jest prostą
prostopadłą do
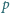 przechodzącą przez
przechodzącą przez
 , przecinającą podstawę
, przecinającą podstawę
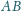 trójkąta w punkcie
trójkąta w punkcie
 , a ramię w punkcie
, a ramię w punkcie
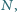 to
to
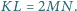
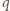 przecina ramię
przecina ramię
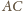 . Rozszerzmy nasz
trójkąt do kwadratu
. Rozszerzmy nasz
trójkąt do kwadratu
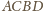 .
.
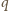 z nowo dorysowanym bokiem kwadratu
oznaczmy przez
z nowo dorysowanym bokiem kwadratu
oznaczmy przez
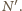 Szukamy takich punktów
Szukamy takich punktów
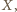 że
że
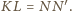 Równoważnie takich, że odcinki
Równoważnie takich, że odcinki
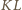 i
i
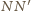 są symetryczne względem prostej
są symetryczne względem prostej
 prostopadłej do
prostopadłej do
 przechodzącej przez
przechodzącej przez
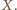 To zachodzi wtedy i tylko wtedy, gdy
trójkąty
To zachodzi wtedy i tylko wtedy, gdy
trójkąty
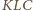 i
i
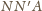 są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
są symetryczne względem tej prostej, co jest
z kolei równoważne temu, że punkty
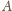 i
i
 są symetryczne
względem
są symetryczne
względem
 (bo punkty
(bo punkty
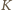 i
i
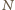 zostały skonstruowane tak,
że są symetryczne względem
zostały skonstruowane tak,
że są symetryczne względem
 ).
).
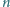 istnieje taka
liczba całkowita dodatnia
istnieje taka
liczba całkowita dodatnia
 , że
, że
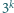 w zapisie dziesiętnym kończy
się cyframi
w zapisie dziesiętnym kończy
się cyframi

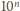 liczb
liczb
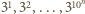 . Żadna z nich nie dzieli się
przez
. Żadna z nich nie dzieli się
przez
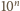 , więc możliwe reszty z dzielenia tych liczb przez
, więc możliwe reszty z dzielenia tych liczb przez
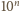 to
to
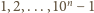 . Jest ich o jeden mniej niż liczb, więc istnieją dwie liczby,
powiedzmy
. Jest ich o jeden mniej niż liczb, więc istnieją dwie liczby,
powiedzmy
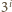 i
i
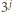 , dla
, dla
 , które dają tę
samą resztę z dzielenia przez
, które dają tę
samą resztę z dzielenia przez
 . Oznacza to, że
. Oznacza to, że
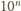 dzieli
dzieli
 . Ale
. Ale
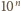 i
i
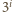 są względnie pierwsze, więc
są względnie pierwsze, więc
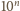 dzieli
dzieli
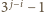 . Zatem
. Zatem
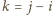 spełnia warunki
zadania.
spełnia warunki
zadania.