O własnościach prostej Simsona»Zadanie 5
o zadaniu...
- Zadanie pochodzi z artykułu O własnościach prostej Simsona
- Publikacja w Delcie: listopad 2016
- Publikacja elektroniczna: 1 listopada 2016
- Artykuł źródłowy w wersji do druku [application/pdf]: (2417 KB)
W trójkącie 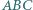 okrąg wpisany jest styczny do boków
okrąg wpisany jest styczny do boków 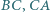 i
i 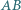 w punktach odpowiednio
w punktach odpowiednio 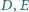 i
i 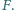 Punkt
Punkt 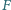 jest punktem Feuerbacha trójkąta
jest punktem Feuerbacha trójkąta 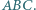 Wówczas prosta Simsona punktu
Wówczas prosta Simsona punktu 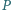 względem trójkąta
względem trójkąta 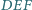 jest równoległa do prostej
jest równoległa do prostej 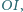 która łączy środki
która łączy środki 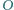 i
i 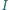 - okręgów opisanego i wpisanego trójkąta
- okręgów opisanego i wpisanego trójkąta 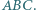
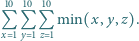
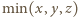 dla wszystkich trójek
dla wszystkich trójek 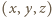 liczb naturalnych nie większych niż
liczb naturalnych nie większych niż 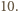
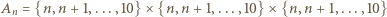
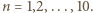 Wówczas
Wówczas 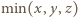 jest równe liczbie sześcianów, do których należy punkt
jest równe liczbie sześcianów, do których należy punkt 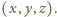 W takim razie
W takim razie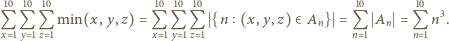
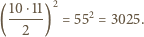
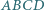 o obwodzie
o obwodzie 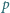 został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie
został podzielony przekątnymi na cztery trójkąty. Środki okręgów wpisanych w te trójkąty tworzą czworokąt o obwodzie 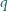 . Wykazać, że pole
. Wykazać, że pole 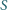 czworokąta
czworokąta 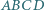 jest mniejsze niż
jest mniejsze niż 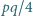 .
.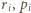 i
i 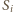 oznaczają dla
oznaczają dla 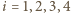 odpowiednio promienie okręgów wpisanych, obwody i pola powstałych czterech trójkątów. Wiemy, że wówczas dla każdego
odpowiednio promienie okręgów wpisanych, obwody i pola powstałych czterech trójkątów. Wiemy, że wówczas dla każdego 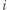 zachodzi równość
zachodzi równość 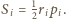 W takim razie
W takim razie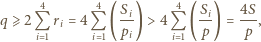
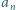 spełnia warunek
spełnia warunek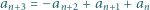
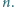 Znaleźć wartość
Znaleźć wartość 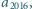 wiedząc, że
wiedząc, że 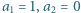 i
i 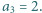
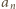 spełnia warunek
spełnia warunek 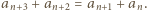 W takim razie
W takim razie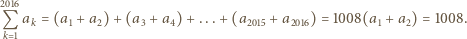
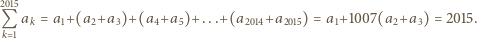
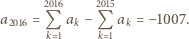
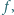 będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do
będąca różnowartościowym odwzorowaniem zbioru wszystkich liczb dodatnich na ten sam zbiór, i taka, że jej pochodna jest funkcją odwrotną do 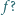
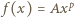 (motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe
(motywacja: zarówno pochodna, jak i funkcja odwrotna do takiej funkcji, też ma taką postać - próba ma szansę powodzenia). Gdy stałe 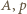 są dodatnie, funkcja
są dodatnie, funkcja 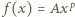 jest ściśle rosnąca i przekształca przedział
jest ściśle rosnąca i przekształca przedział 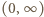 na ten sam przedział. Dla ustalonej wartości
na ten sam przedział. Dla ustalonej wartości 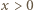 rozwiązujemy równanie
rozwiązujemy równanie 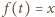 (z niewiadomą
(z niewiadomą 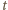 ), otrzymując
), otrzymując 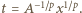 Tak więc
Tak więc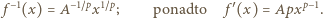
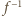 i
i 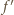 były identyczne, wystarczy, by parametry dodatnie
były identyczne, wystarczy, by parametry dodatnie 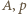 spełniały równania
spełniały równania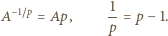
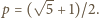 Dla tej stałej
Dla tej stałej 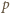 pierwsze równanie przybiera formę
pierwsze równanie przybiera formę 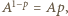 z rozwiązaniem
z rozwiązaniem 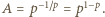 Funkcja
Funkcja 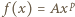 z tymi parametrami ma wymaganą własność.
z tymi parametrami ma wymaganą własność.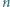 został podzielony (prostymi równoległymi do boków) na
został podzielony (prostymi równoległymi do boków) na 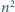 trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.
trójkącików o boku 1. Każdy wierzchołek powstałej siatki (tj. wierzchołek któregoś trójkącika) jest pomalowany na biało lub czarno. Wykonujemy ciąg ruchów. W jednym ruchu zmieniamy kolor wszystkich wierzchołków, leżących na jednej linii prostej, zawierającej bok któregoś trójkącika.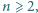 dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.
dla których - wychodząc od stanu: wszystkie wierzchołki białe - można dojść do stanu: dokładnie jeden wierzchołek czarny.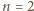 wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny.
wskazany cel da się osiągnąć. W trzech ruchach wybieramy proste zawierające boki dużego trójkąta. Jego wierzchołki pozostaną białe (każdy zmieni kolor dwukrotnie), zaś środki boków staną się czarne. Teraz w jednym ruchu zmieniamy kolor dwóch z tych środków z powrotem na biały. Pozostaje jeden punkt czarny.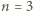 można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni.
można uzyskać wymagany stan. Jak poprzednio, w trzech ruchach bierzemy proste, zawierające boki dużego trójkąta. Jego wierzchołki i jego środek staną się białe, pozostałe punkty siatki staną się czarne. W kolejnych trzech ruchach bierzemy proste równoległe do boków dużego trójkąta i przechodzące przez jego środek. Czarne punkty wybielą się, a punkt w środku się zaczerni. nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym.
nie da się! W trójce punktów, będących wierzchołkami dużego trójkąta, po każdym ruchu jest parzysta liczba czarnych punktów (0 lub 2). Żaden z tej trójki nie może więc być owym punktem, który w pewnym momencie miałby stać się jedynym czarnym.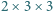 można ułożyć prostopadłościan o wymiarach
można ułożyć prostopadłościan o wymiarach 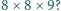
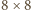 prostopadłościanu
prostopadłościanu 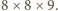 Gdyby dało się zbudować go z opisanych w zadaniu klocków, ściana ta byłaby zbudowana z prostokątów o wymiarach
Gdyby dało się zbudować go z opisanych w zadaniu klocków, ściana ta byłaby zbudowana z prostokątów o wymiarach 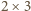 oraz
oraz 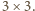 Jednak to jest niemożliwe, gdyż figura złożona z takich prostokątów ma pole podzielne przez 3, a tymczasem ściana
Jednak to jest niemożliwe, gdyż figura złożona z takich prostokątów ma pole podzielne przez 3, a tymczasem ściana 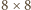 ma pole równe 64.
ma pole równe 64.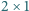 ułożono szachownicę
ułożono szachownicę 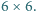 Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.
Wykaż, że istnieje taka prosta równoległa do jednego z boków szachownicy i przechodząca przez jej wnętrze, która nie rozcina żadnej z kostek domina.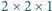 zbudowano sześcian
zbudowano sześcian 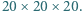 Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.
Wykaż, że istnieje taka prosta równoległa do jednej z krawędzi sześcianu i przechodząca przez jego wnętrze, która nie przecina wnętrza żadnego z klocków.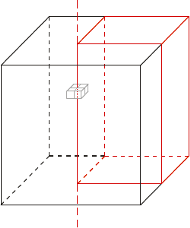
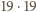 w każdym z trzech kierunków, a więc łącznie
w każdym z trzech kierunków, a więc łącznie 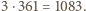
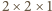 może być przebity przez najwyżej jedną z rozważanych prostych. Gdyby każda z nich przebijała co najmniej dwa klocki, to łącznie przebijałyby one co najmniej
może być przebity przez najwyżej jedną z rozważanych prostych. Gdyby każda z nich przebijała co najmniej dwa klocki, to łącznie przebijałyby one co najmniej 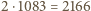 klocków. To także jest niemożliwe, gdyż klocków jest łącznie
klocków. To także jest niemożliwe, gdyż klocków jest łącznie 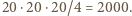 Wobec tego któraś z rozważanych prostych nie przechodzi przez żaden klocek.
Wobec tego któraś z rozważanych prostych nie przechodzi przez żaden klocek.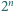 dowolnego spośród
dowolnego spośród 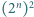 tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami
tworzących go kwadratów jednostkowych powstaje figura, którą daje się szczelnie wypełnić klockami 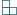 , zbudowanymi z trzech kwadratów jednostkowych.
, zbudowanymi z trzech kwadratów jednostkowych.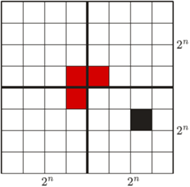
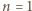 teza jest prawdziwa: rozważana figura jest pojedynczym klockiem. Załóżmy, że teza zachodzi dla pewnego
teza jest prawdziwa: rozważana figura jest pojedynczym klockiem. Załóżmy, że teza zachodzi dla pewnego 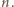 Niech
Niech 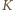 będzie kwadratem o krawędzi
będzie kwadratem o krawędzi 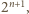 z którego usuwamy jedno pole. Podzielmy
z którego usuwamy jedno pole. Podzielmy 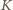 na cztery przystające mniejsze kwadraty o krawędzi
na cztery przystające mniejsze kwadraty o krawędzi 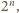 jeden z nich zawiera usunięte pole. Umieśćmy pojedynczy klocek na środku kwadratu
jeden z nich zawiera usunięte pole. Umieśćmy pojedynczy klocek na środku kwadratu 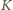 w sposób przedstawiony na rysunku Wówczas na mocy założenia indukcyjnego każdy z czterech mniejszych kwadratów bez jednego pola da się szczelnie wypełnić klockami, co kończy dowód.
w sposób przedstawiony na rysunku Wówczas na mocy założenia indukcyjnego każdy z czterech mniejszych kwadratów bez jednego pola da się szczelnie wypełnić klockami, co kończy dowód.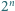 dowolnego spośród
dowolnego spośród 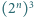 tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami.
tworzących go sześcianów jednostkowych powstaje bryła, którą daje się szczelnie wypełnić klockami. będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita
będzie ustaloną liczbą całkowitą dodatnią. Dowieść, że istnieje nieujemna liczba całkowita 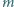 taka, że
taka, że 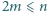 oraz różnica
oraz różnica 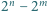 dzieli się przez
dzieli się przez 
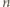 w postaci
w postaci 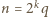 (
( 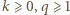 całkowite,
całkowite, 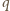 nieparzyste). Znajdujemy wykładnik
nieparzyste). Znajdujemy wykładnik 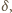 dla którego
dla którego
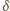 tak, by
tak, by
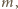 o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci
o jaką pyta zadanie, spróbujemy znaleźć wśród liczb postaci 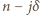 (
( 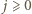 całkowite). Dla
całkowite). Dla 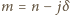 różnica
różnica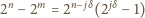
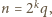 jeśli tylko
jeśli tylko 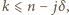 bowiem czynnik w nawiasie dzieli się przez
bowiem czynnik w nawiasie dzieli się przez 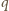 (por. (1)). Biorąc jeszcze pod uwagę wymaganie, by
(por. (1)). Biorąc jeszcze pod uwagę wymaganie, by 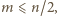 widzimy, że wystarczy znaleźć liczbę
widzimy, że wystarczy znaleźć liczbę 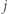 spełniającą nierówność
spełniającą nierówność
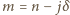 spełni wszystkie żądane warunki.
spełni wszystkie żądane warunki. jest liczbą nieparzystą, czyli gdy
jest liczbą nieparzystą, czyli gdy 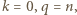 można wziąć
można wziąć 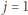 (por. (2)).
(por. (2)). jest liczbą parzystą (więc
jest liczbą parzystą (więc 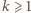 ), warunki (3) postulują istnienie wielokrotności liczby
), warunki (3) postulują istnienie wielokrotności liczby 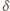 w przedziale
w przedziale ![[n/2,n− k].](/math/temat/matematyka/teoria_liczb/zadania/2016/09/01/zm-k44-726/4x-4209685659c448dfca3440cc75c1cd5715973512-im-66,57,43-FF,FF,FF.gif) Do tego wystarcza, by
Do tego wystarcza, by 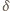 nie przekraczała wartości
nie przekraczała wartości 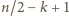 (bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność
(bo tyle jest liczb całkowitych w tym przedziale); a dzięki oszacowaniu (2) wystarczy, by zachodziła nierówność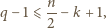
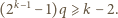

 kąty przy wierzchołkach
kąty przy wierzchołkach 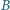 i
i 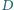 są proste. Przekątne przecinają się w punkcie
są proste. Przekątne przecinają się w punkcie 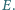 Prosta prostopadła do
Prosta prostopadła do 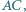 przechodząca przez punkt
przechodząca przez punkt 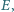 przecina proste
przecina proste 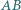 i
i 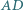 w punktach
w punktach 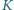 i
i 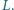 Wykazać, że punkty
Wykazać, że punkty 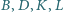 leżą na jednym okręgu.
leżą na jednym okręgu.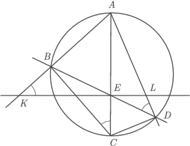
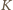 i
i 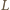 pokrywają się z
pokrywają się z 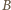 i
i 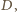 i nie ma czego dowodzić. Przyjmijmy dalej, nie tracąc ogólności, że kąt
i nie ma czego dowodzić. Przyjmijmy dalej, nie tracąc ogólności, że kąt 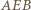 jest ostry (wtedy punkt
jest ostry (wtedy punkt 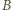 leży między
leży między 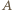 i
i 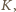 zaś
zaś 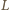 leży między
leży między 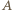 i
i 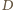 ). Czworokąt
). Czworokąt 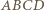 ma okrąg opisany (o średnicy
ma okrąg opisany (o średnicy 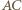 ). Stąd oraz z zależności w trójkątach prostokątnych
). Stąd oraz z zależności w trójkątach prostokątnych 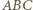 i
i 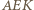 dostajemy ciąg równości
dostajemy ciąg równości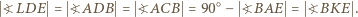
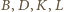 na wspólnym okręgu.
na wspólnym okręgu.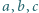 są rozwiązaniami równania
są rozwiązaniami równania 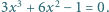 Obliczyć wartość
Obliczyć wartość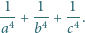
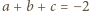 oraz
oraz 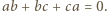 W takim razie mamy również
W takim razie mamy również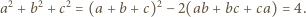
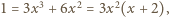 czyli
czyli 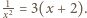 Stąd otrzymujemy
Stąd otrzymujemy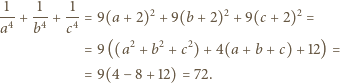
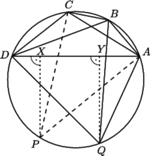
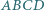 jest takim czworokątem wpisanym w okrąg
jest takim czworokątem wpisanym w okrąg 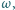 że kąty
że kąty 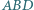 i
i 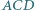 są rozwarte.
są rozwarte. 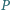 i
i 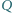 są takimi punktami na dłuższym łuku
są takimi punktami na dłuższym łuku 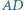 okręgu
okręgu 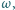 że
że 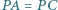 i
i 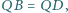 a punkty
a punkty 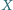 i
i 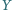 są odpowiednio rzutami prostokątnymi punktów
są odpowiednio rzutami prostokątnymi punktów 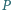 i
i 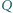 na prostą
na prostą 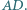 Wiedząc, że odcinki
Wiedząc, że odcinki 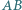 i
i 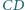 mają odpowiednio długości
mają odpowiednio długości 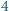 i
i 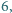 obliczyć długość odcinka
obliczyć długość odcinka 

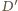 będzie takim punktem na prostej
będzie takim punktem na prostej 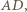 na zewnątrz okręgu
na zewnątrz okręgu 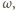 że
że 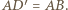 Zauważmy, że wówczas
Zauważmy, że wówczas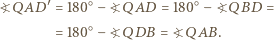
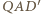 i
i 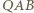 są przystające, w szczególności
są przystające, w szczególności 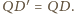 W takim razie trójkąt
W takim razie trójkąt 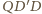 jest równoramienny i
jest równoramienny i 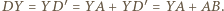
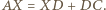 W takim razie mamy
W takim razie mamy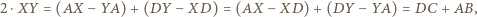
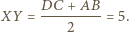
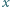 spełniająca równanie
spełniająca równanie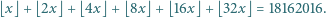
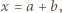 gdzie
gdzie 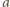 jest pewną liczbą całkowitą oraz
jest pewną liczbą całkowitą oraz 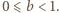 Lewa strona równania przyjmuje postać
Lewa strona równania przyjmuje postać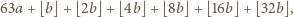
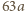 i nie większa niż
i nie większa niż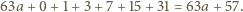
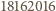 daje resztę
daje resztę 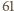 z dzielenia przez
z dzielenia przez 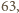 więc nie może być wartością lewej strony równania dla żadnego
więc nie może być wartością lewej strony równania dla żadnego 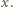
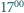 a
a 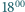 przychodzi na przystanek i wsiada w pierwszy tramwaj, który przyjedzie.
przychodzi na przystanek i wsiada w pierwszy tramwaj, który przyjedzie.
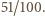
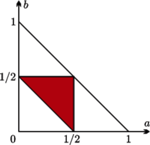
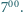 Maja przyjdzie jutro o przypadkowej porze pomiędzy
Maja przyjdzie jutro o przypadkowej porze pomiędzy 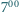 a
a 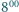 i wsiądzie w pierwszy tramwaj, który przyjedzie. Gucio postąpi tak samo. Z jakim prawdopodobieństwem spotkają się w tramwaju?
i wsiądzie w pierwszy tramwaj, który przyjedzie. Gucio postąpi tak samo. Z jakim prawdopodobieństwem spotkają się w tramwaju?
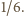
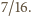
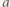 i
i 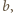 wówczas
wówczas 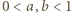 oraz
oraz 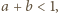 a trzeci fragment ma długość
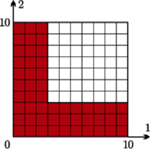
a trzeci fragment ma długość 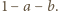 Trójkąt da się zbudować, gdy zachodzą nierówności:
Trójkąt da się zbudować, gdy zachodzą nierówności: 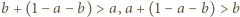 oraz
oraz 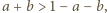 czyli
czyli 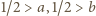 oraz
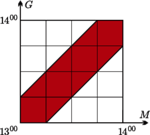
oraz 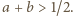 Odpowiada to kolorowemu obszarowi na rysunku obok, a szukane prawdopodobieństwo to stosunek jego pola do pola całej figury zadanej warunkami
Odpowiada to kolorowemu obszarowi na rysunku obok, a szukane prawdopodobieństwo to stosunek jego pola do pola całej figury zadanej warunkami 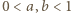 oraz
oraz 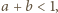 czyli
czyli 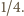
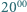 a
a 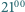 przyjdzie do kawiarni, Gucio postąpi tak samo. Maja wyjdzie po 20 minutach, ale nie później niż o
przyjdzie do kawiarni, Gucio postąpi tak samo. Maja wyjdzie po 20 minutach, ale nie później niż o 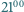 ; Gucio zostanie do
; Gucio zostanie do 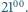 Z jakim prawdopodobieństwem spotkają się?
Z jakim prawdopodobieństwem spotkają się?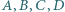 leżą kolejno na okręgu
leżą kolejno na okręgu 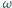 w taki sposób, że cięciwy
w taki sposób, że cięciwy 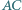 i
i 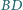 przecinają się pod kątem prostym. Obliczyć promień
przecinają się pod kątem prostym. Obliczyć promień  okręgu
okręgu 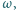 jeśli cięciwy
jeśli cięciwy 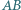 i
i 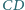 mają odpowiednio długości
mają odpowiednio długości 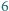 i
i 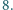
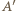 będzie punktem symetrycznym do
będzie punktem symetrycznym do 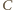 względem środka okręgu. Wówczas
względem środka okręgu. Wówczas 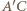 jest średnicą okręgu, więc cięciwa
jest średnicą okręgu, więc cięciwa 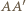 jest prostopadła do odcinka
jest prostopadła do odcinka 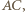 a więc również równoległa do odcinka
a więc również równoległa do odcinka 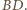 W takim razie
W takim razie 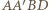 jest trapezem równoramiennym, w szczególności
jest trapezem równoramiennym, w szczególności 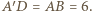 Z twierdzenia Pitagorasa dla trójkąta
Z twierdzenia Pitagorasa dla trójkąta 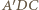 otrzymujemy
otrzymujemy 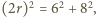 a stąd
a stąd 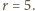
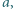 że jej suma cyfr w systemie dziesiętnym jest równa
że jej suma cyfr w systemie dziesiętnym jest równa 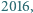 a suma cyfr liczby
a suma cyfr liczby 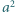 jest równa
jest równa 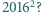
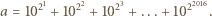
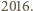 Ponadto
Ponadto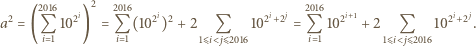
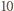 mają parami różne wykładniki. Stąd
mają parami różne wykładniki. Stąd 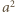 ma w zapisie dziesiętnym
ma w zapisie dziesiętnym 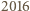 jedynek i
jedynek i 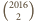 dwójek, czyli suma cyfr
dwójek, czyli suma cyfr 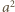 jest równa
jest równa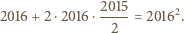
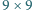 umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.
umieszczono 65 pionków, każdy na innym polu. Co minutę każdy pionek wykonuje ruch na pole sąsiadujące bokiem z polem, na którym się znajduje, w taki sposób, że każde kolejne dwa ruchy pionka mają prostopadłe kierunki. Wykazać, że po pewnym czasie dwa pionki znajdą się na jednym polu.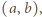 gdzie
gdzie 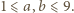 Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
Pomalujmy pola o obu współrzędnych parzystych na niebiesko, pola o obu współrzędnych nieparzystych - na czerwono, a pozostałe pola - na żółto.
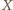 i
i 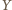 oznaczają odpowiednio punkty przecięcia prostych
oznaczają odpowiednio punkty przecięcia prostych 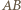 z
z 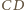 oraz
oraz 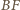 z
z 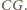 Wówczas każdy z punktów
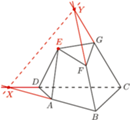
Wówczas każdy z punktów 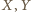 należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty
należy do obu płaszczyzn rozważanych powyżej ścian, a więc też do ich wspólnej prostej. Jednak punkty 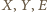 nie są współliniowe, zatem rysunek nie przedstawia wielościanu.
nie są współliniowe, zatem rysunek nie przedstawia wielościanu.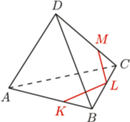
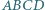 przecięto płaszczyzną, uzyskując w przekroju czworokąt
przecięto płaszczyzną, uzyskując w przekroju czworokąt  Na rysunku obok wyznacz punkt
Na rysunku obok wyznacz punkt  posługując się jedynie linijką.
posługując się jedynie linijką.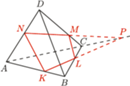
 punkt przecięcia prostych
punkt przecięcia prostych 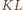 i
i 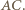 Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta
Punkt ten leży w płaszczyźnie przekroju, zatem leży w niej też prosta 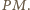 Stąd brakujący punkt
Stąd brakujący punkt 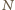 to punkt przecięcia prostych
to punkt przecięcia prostych 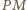 i
i 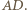
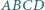 podstawa
podstawa 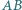 ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt
ma długość 2. Długości pozostałych boków tego trapezu są równe 1. Punkt 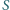 jest wierzchołkiem ostrosłupa o podstawie
jest wierzchołkiem ostrosłupa o podstawie 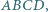 w którym
w którym 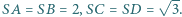 Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.
Wyznacz stosunek objętości tego ostrosłupa do objętości czworościanu foremnego o krawędzi 1.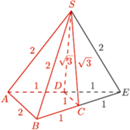
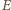 będzie punktem przecięcia prostych
będzie punktem przecięcia prostych 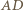 i
i 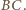 Z kształtu trapezu
Z kształtu trapezu 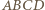 wynika, że
wynika, że 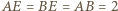 oraz że jego pole to
oraz że jego pole to 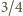 pola trójkąta
pola trójkąta 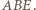
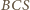 wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ
wnioskujemy, że jest on połową trójkąta równobocznego o krawędzi 2. Ponieważ 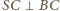 oraz
oraz 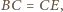 więc
więc 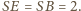
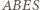 jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest
jest foremny o krawędzi 2. Jego objętość jest zatem 8-krotnie większa od objętości czworościanu foremnego o krawędzi 1, więc szukany stosunek objętości równy jest 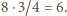
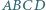 nie będący trapezem. Proste
nie będący trapezem. Proste 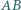 i
i 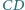 przecinają się w punkcie
przecinają się w punkcie 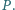 Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu
Wyznacz wszystkie wartości, jakie może przyjąć odległość punktu 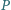 od płaszczyzny podstawy ostrosłupa.
od płaszczyzny podstawy ostrosłupa.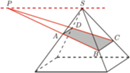
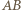 leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta
leży w płaszczyźnie przedniej ściany ostrosłupa z rysunku, a prosta 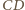 w płaszczyźnie tylnej ściany, więc punkt
w płaszczyźnie tylnej ściany, więc punkt 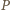 należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek
należy do obydwu tych płaszczyzn. Ich częścią wspólną jest prosta równoległa do podstawy ostrosłupa (gdyż jest on prawidłowy) i przechodząca przez wierzchołek 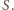 Stąd jedyną wartością, jaką może przyjąć odległość punktu
Stąd jedyną wartością, jaką może przyjąć odległość punktu 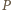 od płaszczyzny podstawy, jest wysokość ostrosłupa równa
od płaszczyzny podstawy, jest wysokość ostrosłupa równa 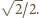
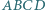 i krawędziach bocznych
i krawędziach bocznych 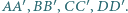 Wyznacz miarę kąta dwuściennego między płaszczyznami
Wyznacz miarę kąta dwuściennego między płaszczyznami 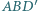 i
i 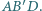
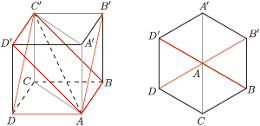
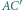
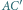
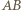 i
i 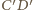 są równoległe, leżą więc w jednej płaszczyźnie
są równoległe, leżą więc w jednej płaszczyźnie 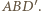 Stąd punkt
Stąd punkt 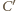 też do niej należy; podobnie należy on także do
też do niej należy; podobnie należy on także do 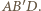 Punkty
Punkty 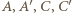 również leżą w jednej płaszczyźnie.
również leżą w jednej płaszczyźnie. i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka
i każda z nich zawiera inną z trzech krawędzi wychodzących z wierzchołka 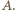 Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po
Oznacza to, że płaszczyzny te tworzą równe kąty dwuścienne, czyli kąty po 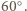
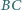 i
i 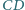 prostokąta
prostokąta 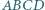 są styczne odpowiednio w punktach
są styczne odpowiednio w punktach 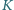 i
i 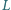 do okręgu przechodzącego przez
do okręgu przechodzącego przez 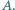 Na odcinku
Na odcinku 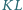 leży taki punkt
leży taki punkt 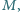 że proste
że proste 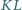 i
i 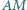 są prostopadłe. Obliczyć pole prostokąta
są prostopadłe. Obliczyć pole prostokąta 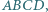 wiedząc, że odcinek
wiedząc, że odcinek 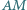 ma długość
ma długość 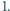
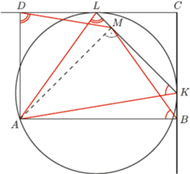
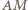 jest prostopadła do
jest prostopadła do 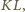 więc jest nachylona do boków prostokąta pod kątem
więc jest nachylona do boków prostokąta pod kątem 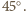 Ponadto kąt środkowy oparty na cięciwie
Ponadto kąt środkowy oparty na cięciwie 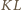 jest prosty, a stąd
jest prosty, a stąd 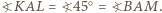
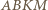 jest opisany na okręgu o średnicy
jest opisany na okręgu o średnicy 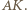 W takim razie kąty
W takim razie kąty 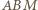 i
i 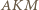 są równe.
są równe.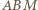 i
i 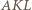 są podobne. Analogicznie trójkąty
są podobne. Analogicznie trójkąty 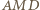 i
i 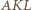 są podobne. W takim razie mamy podobieństwo trójkątów
są podobne. W takim razie mamy podobieństwo trójkątów 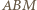 i
i 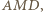 a stąd
a stąd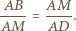
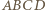 jest równe
jest równe