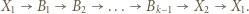Każdego uczestnika turnieju potraktujmy jako wierzchołek, a każdy mecz jako krawędź pewnego grafu skierowanego 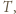 skierowaną od zwycięzcy do przegranego. Usadzenie
skierowaną od zwycięzcy do przegranego. Usadzenie 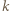 zawodników przy okrągłym stole zgodnie z warunkami zadania jest równoważne istnieniu skierowanego cyklu długości
zawodników przy okrągłym stole zgodnie z warunkami zadania jest równoważne istnieniu skierowanego cyklu długości 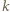 (krótko:
(krótko: 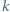 -cyklu).
-cyklu).
Udowodnimy, że:
- w
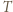 istnieje 3-cykl;
istnieje 3-cykl;
- jeśli w
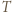 istnieje
istnieje 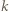 -cykl, to istnieje też
-cykl, to istnieje też 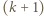 -cykl, dla
-cykl, dla 
Wyniknie stąd, że w 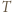 istnieje
istnieje 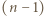 -cykl, czyli teza zadania.
-cykl, czyli teza zadania.
Niech 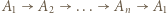 będzie wyjściowym
będzie wyjściowym  -cyklem oraz niech
-cyklem oraz niech 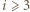 będzie najmniejszym indeksem o tej własności, że
będzie najmniejszym indeksem o tej własności, że 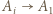 (zbiór takich indeksów jest niepusty, gdyż należy do niego
(zbiór takich indeksów jest niepusty, gdyż należy do niego  ). Wówczas
). Wówczas 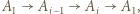 więc w
więc w 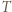 istnieje 3-cykl.
istnieje 3-cykl.
Niech 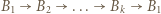 będzie pewnym
będzie pewnym 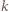 -cyklem, gdzie
-cyklem, gdzie 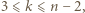 oraz niech
oraz niech 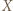 będzie dowolnym wierzchołkiem spoza tego cyklu. Jeśli istnieje takie
będzie dowolnym wierzchołkiem spoza tego cyklu. Jeśli istnieje takie 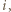 że
że 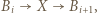 to uzyskujemy
to uzyskujemy 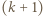 -cykl poprzez wstawienie
-cykl poprzez wstawienie 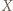 pomiędzy
pomiędzy 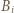 oraz
oraz 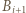 (przyjmujemy
(przyjmujemy 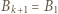 ). W przeciwnym przypadku są dwie możliwości:
). W przeciwnym przypadku są dwie możliwości: 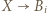 dla każdego
dla każdego 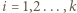 lub
lub 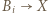 dla każdego
dla każdego 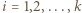 ; niech
; niech 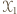 będzie zbiorem wierzchołków
będzie zbiorem wierzchołków 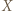 pierwszego typu, a
pierwszego typu, a 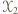 - zbiorem wierzchołków
- zbiorem wierzchołków 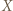 drugiego typu.
drugiego typu.
Gdyby 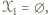 to
to 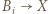 dla każdego
dla każdego 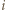 oraz każdego
oraz każdego 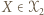 - nie mógłby wtedy jednak istnieć
- nie mógłby wtedy jednak istnieć 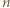 -cykl w
-cykl w 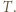 Podobnie gdyby
Podobnie gdyby 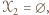 to w
to w 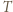 nie mógłby istnieć
nie mógłby istnieć 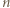 -cykl. Również gdyby
-cykl. Również gdyby 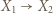 dla każdej pary
dla każdej pary 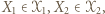 to w
to w 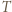 nie mógłby istnieć
nie mógłby istnieć 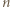 -cykl. Stąd wniosek, że istnieją wierzchołki
-cykl. Stąd wniosek, że istnieją wierzchołki 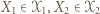 o tej własności, że
o tej własności, że 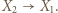 To oznacza, że istnieje
To oznacza, że istnieje 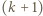 -cykl
-cykl
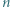 osób
osób 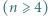 . Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z nich. Po turnieju wszyscy usiedli przy okrągłym stole w taki sposób, że każdy wygrał z osobą siedzącą bezpośrednio po swojej prawej stronie. Wykazać, że można tak pewną osobę wyprosić, a pozostałe przesadzić, aby ta własność pozostała zachowana, tzn. każdy miał na prawo osobę, z którą wygrał.
. Każda para osób rozegrała dokładnie jeden mecz, który zakończył się zwycięstwem jednej z nich. Po turnieju wszyscy usiedli przy okrągłym stole w taki sposób, że każdy wygrał z osobą siedzącą bezpośrednio po swojej prawej stronie. Wykazać, że można tak pewną osobę wyprosić, a pozostałe przesadzić, aby ta własność pozostała zachowana, tzn. każdy miał na prawo osobę, z którą wygrał.
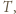
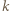
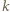 (krótko:
(krótko: 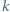 -cyklu).
-cyklu).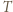
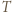
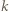 -cykl, to istnieje też
-cykl, to istnieje też 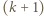 -cykl, dla
-cykl, dla 
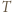
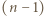 -cykl, czyli teza zadania.
-cykl, czyli teza zadania.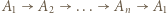
 -cyklem oraz niech
-cyklem oraz niech 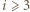
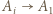 (zbiór takich indeksów jest niepusty, gdyż należy do niego
(zbiór takich indeksów jest niepusty, gdyż należy do niego  ). Wówczas
). Wówczas 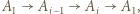
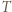
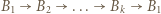
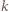 -cyklem, gdzie
-cyklem, gdzie 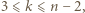
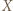
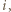
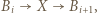
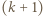 -cykl poprzez wstawienie
-cykl poprzez wstawienie 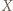
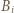
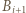 (przyjmujemy
(przyjmujemy 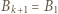 ). W
). W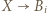
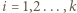
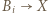
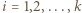 ; niech
; niech 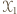
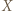
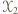 - zbiorem wierzchołków
- zbiorem wierzchołków 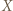
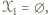
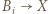
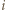
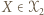 - nie mógłby wtedy jednak istnieć
- nie mógłby wtedy jednak istnieć 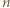 -cykl w
-cykl w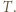
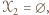
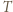
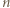 -cykl. Również gdyby
-cykl. Również gdyby 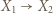
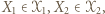
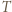
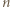 -cykl. Stąd wniosek, że istnieją wierzchołki
-cykl. Stąd wniosek, że istnieją wierzchołki 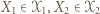
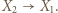
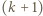 -cykl
-cykl