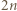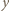Zauważmy, że każdy delfin wykonał dokładnie 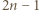 skoków, a zatem żaden z nich nie mógł opłynąć całego basenu. Dla każdego delfina rozważmy skierowany łuk basenu rozpoczynający się w początkowym zbiorniku delfina, a kończący w jego zbiorniku końcowym. Jeżeli delfin wykonał
skoków, a zatem żaden z nich nie mógł opłynąć całego basenu. Dla każdego delfina rozważmy skierowany łuk basenu rozpoczynający się w początkowym zbiorniku delfina, a kończący w jego zbiorniku końcowym. Jeżeli delfin wykonał  skoków zgodnie z ruchem wskazówek zegara (patrząc na basen od góry), to wykonał
skoków zgodnie z ruchem wskazówek zegara (patrząc na basen od góry), to wykonał 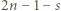 skoków w przeciwnym kierunku, a zatem jego łuk ma skierowaną długość
skoków w przeciwnym kierunku, a zatem jego łuk ma skierowaną długość 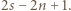 Łączna długość wszystkich takich łuków jest równa zero, gdyż przy każdej akrobacji długość łuku jednego z uczestniczących w niej delfinów wzrasta o 1, a drugiego - maleje o 1.
Łączna długość wszystkich takich łuków jest równa zero, gdyż przy każdej akrobacji długość łuku jednego z uczestniczących w niej delfinów wzrasta o 1, a drugiego - maleje o 1.
Niech  będzie delfinem, który wykonał najwięcej skoków zgodnie z ruchem wskazówek zegara, czyli równoważnie - ma najdłuższy łuk. Zauważmy, że delfin
będzie delfinem, który wykonał najwięcej skoków zgodnie z ruchem wskazówek zegara, czyli równoważnie - ma najdłuższy łuk. Zauważmy, że delfin  skakał wyłącznie zgodnie z ruchem wskazówek zegara. Rzeczywiście, gdyby
skakał wyłącznie zgodnie z ruchem wskazówek zegara. Rzeczywiście, gdyby  skoczył w przeciwnym kierunku podczas wspólnej akrobacji z delfinem
skoczył w przeciwnym kierunku podczas wspólnej akrobacji z delfinem 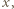 to oznaczałoby, że początkowo
to oznaczałoby, że początkowo 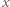 znajdował się we (zegarowo) wcześniejszym zbiorniku, a końcowo w późniejszym, gdyż była to ich jedyna zamiana. W konsekwencji łuk
znajdował się we (zegarowo) wcześniejszym zbiorniku, a końcowo w późniejszym, gdyż była to ich jedyna zamiana. W konsekwencji łuk 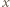 byłby dłuższy niż łuk
byłby dłuższy niż łuk 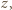 co jest sprzeczne z wyborem
co jest sprzeczne z wyborem 
Oznaczmy zbiorniki kolejno liczbami 1, 2, 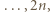 zgodnie z ruchem wskazówek zegara, przy czym 1 jest początkowym zbiornikiem delfina
zgodnie z ruchem wskazówek zegara, przy czym 1 jest początkowym zbiornikiem delfina 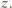 Skoro
Skoro  wykonał dokładnie
wykonał dokładnie 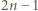 skoków i w każdym z nich numer zbiornika wzrastał o 1, to końcowym zbiornikiem
skoków i w każdym z nich numer zbiornika wzrastał o 1, to końcowym zbiornikiem  jest
jest 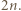 Wykażemy, że obręcz między zbiornikami 1 oraz
Wykażemy, że obręcz między zbiornikami 1 oraz 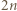 nie została użyta do wykonania żadnej akrobacji.
nie została użyta do wykonania żadnej akrobacji.
Przypuśćmy przeciwnie - że w pewnym momencie delfin 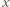 znajdujący się w zbiorniku 1 zamienił się z delfinem
znajdujący się w zbiorniku 1 zamienił się z delfinem 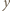 znajdującym się w zbiorniku
znajdującym się w zbiorniku 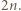 Ich położenie świadczy o tym, że
Ich położenie świadczy o tym, że  zamienił się już wcześniej z
zamienił się już wcześniej z 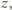 a
a 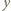 - jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i
- jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i 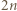 zamiana delfinów
zamiana delfinów 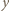 i
i  przestanie być możliwa, gdyż
przestanie być możliwa, gdyż  skacze tylko zgodnie z ruchem wskazówek zegara. Uzyskana sprzeczność kończy rozwiązanie.
skacze tylko zgodnie z ruchem wskazówek zegara. Uzyskana sprzeczność kończy rozwiązanie.
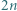 małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami
małych zbiorników poprzedzielanych zawieszonymi nad wodą obręczami 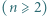 . W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
. W każdym małym zbiorniku (znajdującym się pomiędzy dwiema obręczami) pływa jeden delfin. Co jakiś czas dwa delfiny z sąsiednich zbiorników wykonują akrobację polegającą na jednoczesnym skoku przez obręcz (znajdującą się między zbiornikami) i w rezultacie - zamianie miejscami. Przypuśćmy, że po pewnym czasie każde dwa delfiny zamieniły się miejscami dokładnie raz. Wykazać, że pewna obręcz nie została użyta do wykonania żadnej akrobacji.
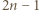

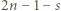
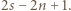



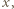
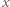

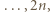

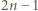

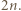
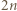
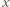
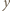
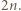

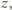
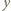 - jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i
- jeszcze nie. Jednak po skoku przez obręcz między zbiornikami 1 i