Diagramy Venna
W tym artykule zajmiemy się nieco dokładniej diagramami Venna.
W tym artykule zajmiemy się nieco dokładniej diagramami Venna.
Gry, zagadki, paradoksy Gammalimatias
Używanie średnich jest tyleż proste co niebezpieczne...
Moja rodzina lubi pizzę, a ja lubię ją piec. Jednak w naszej gromadce nikt nie lubi jeść takiej samej pizzy, jak pozostali członkowie rodziny. Jest nas tylko czworo, więc można sobie z tym poradzić bez trudu, używając tylko dwóch składników – typowa pizza wygląda więc tak...
Rachunek prawdopodobieństwa Omega
Rachunek prawdopodobieństwa Mała Delta
Jeden z bardzo znanych matematyków stwierdził niedawno, że matematyka to tak naprawdę część fizyki, wyróżniająca się tylko tym, że eksperymenty są w niej bardzo tanie.
Tangram to stara chińska zabawa, polegająca na układaniu zadanych figur z siedmiu klocków, ułożonych na rysunku 1 w kwadrat.
W numerze poświęconym mierze (8/2008) nie sposób pominąć tych pierwszych, czyli zwykłych miar geometrycznych (zważmy, że geometria ma miarę w swojej nazwie).Wydaje się, że wiemy o nich wszystko, bo przecież stykaliśmy się z nimi niemal od zerówki. Okazuje się jednak, że i na ich temat można postawić pytania o nieoczywistych odpowiedziach.
Korzenie teorii miary sięgają tak podstawowych pojęć, jak długość (np.
odcinka), pole (np. koła) i objętość (np. kuli). Wraz z rozwojem matematyki
konieczne stało się uogólnienie tych pojęć w taki sposób, żeby dało się
„zmierzyć” coraz bardziej skomplikowane podzbiory danej przestrzeni – na przykład
prostej rzeczywistej
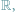 do której w tym artykule ograniczymy nasze
rozważania.
do której w tym artykule ograniczymy nasze
rozważania.
Rachunek prawdopodobieństwa Co to jest?
Jak wiadomo, komputery traktują wszystkie dane, na których działają, jako ciągi bitów,
z których każdy może mieć dwie wartości (0 lub 1). Przykładowo, ten
tekst jest zapisany w ten sposób, że każdej z liter i pozostałych znaków
odpowiada ciąg 8 bitów. Daje to
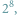 czyli 256 możliwości, co w zupełności
wystarcza do zapisania wszystkich potrzebnych znaków. Jednak w rzeczywistości
różnych znaków występujących w tekście jest mniej. Problem jest więc
taki: jak zapisać tekst tak, żeby na każdą jego literę przypadało jak najmniej
bitów?
czyli 256 możliwości, co w zupełności
wystarcza do zapisania wszystkich potrzebnych znaków. Jednak w rzeczywistości
różnych znaków występujących w tekście jest mniej. Problem jest więc
taki: jak zapisać tekst tak, żeby na każdą jego literę przypadało jak najmniej
bitów?
Jednym z podstawowych sposobów mierzenia zbioru jest liczenie jego elementów.
Liczenie ma jednak jasny sens tylko dla zbiorów skończonych. Wiadomo, co to znaczy,
że jakiś zbiór ma
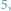
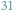 czy
czy
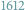 elementów. W przypadku
zbiorów nieskończonych sytuacja jest natomiast znacznie mniej oczywista. Czy
zbiorowi nieskończonemu da się w ogóle przypisać liczbę elementów sensowniej
niż przez uznanie, że wynosi ona zawsze
elementów. W przypadku
zbiorów nieskończonych sytuacja jest natomiast znacznie mniej oczywista. Czy
zbiorowi nieskończonemu da się w ogóle przypisać liczbę elementów sensowniej
niż przez uznanie, że wynosi ona zawsze
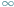 ?
?
Rachunek prawdopodobieństwa Konkurs prac uczniowskich
Jednym z najbardziej znanych zagadnień prawdopodobieństwa geometrycznego
jest problem igły Buffona. Treść tego zadania zna wiele osób, które, nawet
jeśli nie znają sposobu rozwiązania, to wiedzą, że jest ono związane z liczbą
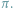
Koło Matematyków Studentów UJ im. prof. Stanisława Zaremby powstało w XIX wieku, pod nazwą Kółko Matematyczno-Fizyczne Uczniów UJ. „Zebranie przedwstępne” odbyło się 3 grudnia 1893.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Joseph Louis Lagrange (1736--1813) był ogromnie zniesmaczony ciągle nieudanymi próbami ścisłego zdefiniowania koniecznego dla zastosowań matematyki pojęcia pochodnej funkcji. Rzecz udawała się właściwie tylko dla wielomianów.
Nie wiem, czy wielu Czytelników Delty słyszało o szczęśliwych liczbach. Nie chodzi tu o to, że często siódemkę uważa się za liczbę szczęśliwą, trzynastkę zaś za pechową, ale o matematyczne pojęcie.
Prawie dwieście lat temu Augustin Cauchy udowodnił, że wielościan wypukły, który ma sztywne ściany, jest cały sztywny, choćby jego krawędzie były wyposażone w najlepsze zawiasy. I postawił problem, czy założenie wypukłości jest konieczne.
Analiza Stowarzyszenie na rzecz Edukacji Matematycznej
W wielu zadaniach dane są trzy proste, które albo przecinają się w jednym punkcie, albo należy to o nich udowodnić. Wygodnym narzędziem bywa wtedy twierdzenie Cevy.
Polski namiot na francuskim Festiwalu Nauki był tak pełen gości, że miejsce dla jego matematycznej części życzliwie zostało ofiarowane przez Jeana Brette’a i jego kolegów w namiocie Pałacu Odkryć.
Najpierw należy odpowiedzieć na pytanie: co to jest matematyka? Są dwie odpowiedzi: otwarty, stale uzupełniany, zasób rozumowań, albo nauka poznawcza badająca pewne abstrakcyjne twory przy użyciu rozumowań jako narzędzia badawczego.
Matematyka Stowarzyszenie na rzecz Edukacji Matematycznej
W roku szkolnym 2010/2011 odbywa się szósta edycja Olimpiady Matematycznej Gimnazjalistów. Jest to już od kilku lat najbardziej prestiżowy ogólnopolski konkurs matematyczny dla uczniów gimnazjów.
Czy przyszło Wam kiedyś do głowy, drodzy Czytelnicy, mierzyć nitką objętość? Albo pole?
W matematyce, z jaką spotykamy się w szkole i na uniwersytecie, linię prostą identyfikuje się ze zbiorem punktów, w którym współrzędnymi są liczby rzeczywiste. Istnieje jednakże argument przeciw takiemu konkretnemu utożsamieniu, który opiera się na tym, iż nieskończenie wiele własności linii prostej nie może być ani dowiedzionych, ani obalonych za pomocą aksjomatów używanych w teorii mnogości (tzw. aksjomatów Zermelo–Fraenkla).