Delta mi!

W dzisiejszym świecie ludzie stają się coraz bardziej leniwi. Chcą osiągnąć zysk w krótkim czasie, bez zbytecznej pracy. Najłatwiejszym sposobem na „zarabianie” są gry. Ale czym właściwie jest gra?

Około 1930 roku Richard Rado (1906-1989) postawił następujący problem: Lew 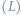 i człowiek 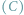– traktowani jako punkty – poruszają się w domkniętym kole jednostkowym z jednakowymi maksymalnymi prędkościami. Czy (głodny) lew zawsze złapie człowieka?

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Legenda powiada, że gdy bóg Brahma po raz pierwszy poruszył czas, umieścił na jednej z trzech diamentowych igieł, umocowanych na wspólnej podstawce, 64 złote krążki. Na podstawce spoczywał krążek najszerszy, a nad nim lśniły pozostałe o coraz mniejszych średnicach. Bóg polecił mnichom z górskiej samotni, by bez spoczynku przekładali krążki, tak aby wszystkie znalazły się na drugiej diamentowej igle, z zachowaniem tego samego ułożenia. Gdy zadanie zostanie zakończone, nastąpi koniec pierwszego świata, a na następny, wskrzeszony przez Brahmę, wypadnie czekać wiele tysięcy lat...

Gdzie na płaszczyźnie znajdują się punkty, których stosunek odległości do dwóch ustalonych punktów 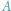 i 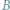 równy jest danej dodatniej stałej

Zaczęło się od okręgu. Wykres funkcji sinus okazał się okręgiem. Jak to możliwe? Okazuje się, że czasem lekkie odstąpienie od utartego punktu widzenia może nas daleko zaprowadzić. Wystarczy, na przykład, wybrać inny niż prostokątny układ współrzędnych do przedstawiania wykresów funkcji.

Pod koniec lata 2012 roku wśród matematyków rozeszła się wiadomość, że 21 sierpnia zmarł William Thurston, matematyk, laureat medalu Fieldsa. Gdy w październiku 2010 roku zmarł Benoît Mandelbrot, pisały o tym niemal wszystkie gazety, informowały portale społecznościowe. O śmierci Thurstona dowiedzieli się – jak to najczęściej bywa w przypadku matematyków – głównie specjaliści. William Thurston zasłynął z postawienia, pod koniec lat siedemdziesiątych XX stulecia, hipotezy geometryzacyjnej i prób jej udowodnienia. Za te osiągnięcia, a miał jeszcze wiele innych, został uhonorowany medalem Fieldsa na Międzynarodowym Kongresie Matematyków w Warszawie w 1983 roku.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Wyobraźmy sobie następującą grę. Na stole w jednym rzędzie leży  monet o różnych nominałach. Dwoje graczy – Ania i Bartek – wykonuje na przemian ruchy, zaczyna Ania. Ruch polega na zabraniu jednej monety z lewego lub prawego końca rzędu. Wynikiem gry jest, oczywiście, suma nominałów monet zgromadzonych przez każdego z graczy. Jak powinna grać Ania, by uzyskać jak największą sumę, jeśli wie ona, że Bartek będzie grał optymalnie (tzn. będzie starał się zmaksymalizować swoją sumę)?

Matematycy od wielu lat zajmują się wędrówką po okręgu. Jednym z najbardziej znanych przykładów jest chyba skakanie po nim w określonym kierunku tak, by między kolejnymi punktami, w których się znajdziemy, była określona odległość  (mierzona wzdłuż łuku). Naturalne staje się wówczas pytanie, czy skacząc tak po okręgu, wrócimy kiedykolwiek do punktu wyjścia (widać, że rozwiązanie problemu nie zależy od punktu startowego)? Odpowiedź nasuwa się prędko – powrót nastąpi tylko wówczas, gdy stosunek długości okręgu do liczby  jest liczbą wymierną. Spróbujmy tym razem powędrować w inny sposób, określony geometrycznie.

Kiedy na płaszczyźnie mamy do czynienia z okręgami, to bardzo często posługujemy się rachunkiem na kątach, ponieważ znamy wiele przydatnych twierdzeń i faktów z tego zakresu. Niestety, trudno o analogiczne narzędzia w przestrzeni. Stanowi to wielki kłopot, gdy zmagamy się z zadaniami o sferach. Istnieje jednak kilka innych technik, skutecznych w zadaniach o okręgach, które działają również w przestrzeni. Są to: potęga punktu, jednokładność oraz inwersja. O tej ostatniej metodzie opowiemy w tym kąciku.

Spójrzmy na cztery z pozoru zupełnie niezwiązane zadania...

Miniony rok przyniósł znaczący wzrost zainteresowania Olimpiadą Matematyczną Gimnazjalistów, a towarzyszył mu szereg inicjatyw Komitetu Głównego mających na celu rzeczone zainteresowanie utrzymać. Jedną z nich było powołanie do życia gazetki Kwadrat, na łamach której znajdują się przeznaczone dla gimnazjalistów artykuły matematyczne oraz wiadomości dotyczące organizacji OMG.

Pewnego grudniowego wieczoru Genowefa zaproponowała swojej siostrze Zenobii...

Komitet Noblowski zadecydował o przyznaniu Nagrody w dziedzinie nauk ekonomicznych za rok 2012 Lloydowi Shapley’owi i Alvinowi Rothowi. Nagrody z ekonomii nie są, ściśle rzecz ujmując, Nagrodami Nobla, bo gdy wynalazca dynamitu ustanawiał prestiżowe wyróżnienia, żadnej z nauk społecznych nie uznawano za wystarczająco rozwiniętą. Od roku 1969 są jednak przyznawane Nagrody z ekonomii ufundowane przez Bank Szwecji, ekonomiści są zatem i tak w lepszym położeniu niż matematycy...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Niejeden maturzysta marzy zapewne, żeby na egzaminie dojrzałości rozwiązywać następujące, z pozoru błahe, zadanie: Wyznacz liczbę miejsc zerowych funkcji 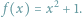Abiturienta nie zraziłaby prawdopodobnie nawet drobna przeszkoda, jaką jest wyraźny brak informacji o dziedzinie funkcji 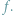 Z uwagi na wszechobecność zbioru liczb rzeczywistych w obecnym programie nauczania wydaje się, że o żadnych zerach mowy być nie może. Nawet słynna „delta” nie jest tu potrzebna.

W roku szkolnym 2011/2012 zmieniona została formuła Olimpiady Matematycznej Gimnazjalistów. Zmiana ta zaowocowała znacznym wzrostem zainteresowania Olimpiadą. W związku z tym Komitet Główny Olimpiady Matematycznej Gimnazjalistów oraz Stowarzyszenie na rzecz Edukacji Matematycznej zorganizowały w całej Polsce cykl seminariów Poznajemy Olimpiadę Matematyczną Gimnazjalistów.

W wielu problemach matematycznych warto rozważać elementy ekstremalne – największe, najkrótsze, najbliższe... Metoda ta bywa często przydatna w zadaniach dotyczących punktów płaszczyzny lub grafów, czyli punktów łączonych liniami.

W pierwszym tygodniu lipca 2012 roku w Krakowie gościł VI Europejski Kongres Matematyczny (takie kongresy organizowane są od 1992 roku co 4 lata; poprzednie odbyły się w Paryżu, Budapeszcie, Barcelonie, Sztokholmie i Amsterdamie). Przyznano na nim dziesięć nagród Europejskiego Towarzystwa Matematycznego (dalej w skrócie EMS), przeznaczonych dla osób, które w wieku co najwyżej 35 lat mają błyskotliwe osiągnięcia matematyczne.