Algebra Kącik początkującego olimpijczyka
Twierdzenie Bézouta
O licznych zastosowaniach faktu, że dla każdego wielomianu 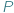 w sumie algebraicznej
w sumie algebraicznej 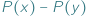 można wyłączyć przed nawias wyrażenie
można wyłączyć przed nawias wyrażenie 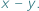
Algebra Kącik początkującego olimpijczyka
O licznych zastosowaniach faktu, że dla każdego wielomianu 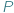 w sumie algebraicznej
w sumie algebraicznej 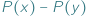 można wyłączyć przed nawias wyrażenie
można wyłączyć przed nawias wyrażenie 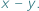
Czytelnicy Delty zapewne znają zawody matematyczne dla uczniów, takie jak Olimpiada Matematyczna lub Kangur Matematyczny. Nie wszyscy wiedzą jednak, że konkursowe zmagania można kontynuować również podczas studiów. Na niektórych uczelniach odbywają się nawet specjalne zajęcia, podczas których rozwiązuje się i omawia zadania konkursowe.
Choć ruch jest wszechobecny w naszym otoczeniu, to opis dynamicznych zmian będących jego wynikiem sprawia nam kłopot. Oto kilka prostych obserwacji...
W październikowym numerze Delty przedyskutowaliśmy hipotezę continuum i zaskakujące rozwiązanie problemu dotyczącego jej prawdziwości (o ile Czytelnik zgodzi się nazwać to rozwiązaniem). Na pytanie, czy istnieje nieskończony podzbiór zbioru liczb rzeczywistych, który nie jest równoliczny ze zbiorem liczb naturalnych ani ze zbiorem wszystkich liczb rzeczywistych (jest więc "większy" od zbioru liczb naturalnych, ale "mniejszy" od zbioru liczb rzeczywistych), odpowiedź nie brzmi "tak" ani "nie". Okazało się, że nie jest możliwe udowodnienie, że taki zbiór istnieje, ani że taki zbiór nie istnieje...
Zastosowania matematyki Epidemie
Czy lubicie długoterminowe prognozy pogody? Odbija się w nich głęboko zakorzeniona ludzka wiara, że odległą przyszłość można przewidzieć - na przekór efektowi motyla. No cóż, sam muszę przyznać, że cieszę się, gdy grudniowe prognozy przewidują piękną, słoneczną i mroźną aurę na zimowe ferie; ale jeśli zapowiadają ponury mokry standard, wtedy ratuję się myślą, że to przecież tylko prognoza...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Planimetria Kącik początkującego olimpijczyka
Przedstawiamy wygodne narzędzie geometryczne o wielu zastosowaniach, wśród których znajduje się dowodzenie współliniowości punktów.
Nagraliśmy ze znajomymi piosenkę. Nie było to profesjonalne przedsięwzięcie: nie wynajęliśmy studia nagraniowego, ale spotkaliśmy się u jednego z nas, wyjęliśmy instrumenty i zagraliśmy kilka razy do porządnego dyktafonu. Niestety, brak zawodowstwa dało się odczuć natychmiast - okazało się, że siedziałem na skrzypiącym krześle, które przy każdym moim ruchu robiło ziiik, ziiiiiik. Skrzypienie, choć nie permanentne, stanowczo utrudniało percepcję.
Teoria liczb to prawdopodobnie najstarsza dziedzina wiedzy matematycznej, badana intensywnie już w czasach starożytnych (a zapewne jeszcze wcześniej; możliwe, że nawet zanim powstała jakakolwiek cywilizacja operująca przekazem pisemnym).
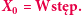 W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.
W roku 2009 słowem dziesięciolecia stowarzyszenie American Dialect Society ogłosiło czasownik to google, którego polski odpowiednik - guglować/guglać - omawiany jest już na stronach Słownika Języka Polskiego, PWN. Nic dziwnego, wszak korzystanie z wyszukiwarki Google stało się elementem codzienności większości z nas i nie mamy skrupułów przed zadawaniem jej pytań o najbłahsze sprawy. Idąc za myślą przewodnią tego numeru Delty, o nieoczekiwanych związkach teorii z rzeczywistością, pokażemy, co wspólnego ma wszędobylska wyszukiwarka z teorią łańcuchów Markowa, sformułowaną w początkach XX wieku.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Algebra Kącik początkującego olimpijczyka
O stosowaniu podstawowej wiedzy szkolnej na temat funkcji kwadratowej do rozwiązywania zadań olimpijskich.
W dniach 6-9 czerwca w Szczyrku odbył się XXXVI Ogólnopolski Sejmik Matematyków, organizowany przez Pracownię Matematyki i Informatyki Pałacu Młodzieży w Katowicach we współpracy z Uniwersytetem Śląskim.
Teoria Mnogości Nieskończoność
W tym odcinku zajmiemy się hipotezą continuum.
Gry, zagadki, paradoksy Ogródek Gardnera
Pokazy iluzjonistyczne nacechowane są elementami odwracającymi uwagę, nadzwyczajną zwinnością, sprawnością ruchową lub rachunkową iluzjonisty. Dla nas, matematyków, najciekawsze są oczywiście te wykorzystujące pewne aspekty matematyki. Przedstawimy kilka trików, które łączy wspólne ogniwo - systemy pozycyjne.
Tym razem o kilku ciekawych własnościach funkcji Eulera.
Niech autorowi będzie wolno cofnąć się w czasy lśniących w słońcu chromowanych obręczy kół rowerów (lub wózków dziecinnych). Obręcze te rzucały rozmaite odblaski na powierzchnię szosy. Bogactwo obserwowanych kształtów zachęcało do podjęcia próby opisania ich w języku matematyki. Zróbmy to teraz, choć poniewczasie - bo współcześnie trudniej o okazję ujrzenia tego zjawiska.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Planimetria Kącik początkującego olimpijczyka
Gdy w zadaniu występuje kąt o mierze będącej wielokrotnością 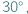 to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
to jest spora szansa na to, że gdzieś tam jest ukryty trójkąt równoboczny.
W pierwszej połowie XX wieku znaczący postęp prac nad matematycznymi modelami zjawisk losowych doprowadził do powstania wyodrębnionego działu matematyki wykorzystującego zaawansowane metody algebry i analizy matematycznej. Tematów badawczych dostarczały pytania stawiane przez specjalistów różnych dziedzin. Abstrahowanie od szczegółowych cech badanych zjawisk w procesie modelowania matematycznego niejednokrotnie prowadziło do zbliżonych opisów różnych zagadnień. Dzisiaj mówimy o zastosowaniach rachunku prawdopodobieństwa, które posiłkują się teorią procesów stochastycznych i statystyką. Jednolity model matematyczny stawał się także narzędziem do wykorzystania przy badaniu zagadnień, do analizy których nie wykorzystywano wcześniej metod matematycznych...
Tytuł niniejszego artykułu jest zestawieniem dwóch pozornie odległych pojęć matematycznych. Pierwszym z nich jest trójkąt Sierpińskiego - jeden z najlepiej rozpoznawalnych fraktali. Drugim jest gra w życie - automat komórkowy opisany w 1970 roku przez Johna Conwaya.
Modelowanie matematyczne jest pewnego rodzaju sztuką opisywania świata - zarówno w skali mikro, jak i makro - za pomocą równań matematycznych (równań różniczkowych, różnicowych czy stochastycznych). Opis mikroskopowy może dotyczyć zachowania pojedynczych molekuł (cząsteczek), natomiast obiektem opisu makroskopowego jest to, co widzimy "gołym okiem", m.in. przemiany zachodzące w wyniku reakcji chemicznych. Mogą to być zmiany właściwości fizycznych danych substancji (np. stan skupienia, barwa, gęstość) lub chemicznych (np. zapach, smak, toksyczność)...

W artykule rozważymy geometryczny problem, do którego sformułowania użyjemy motywacji astronomicznych. Załóżmy, że chcemy sprawdzić, czy najbliższa naszej intuicji szkolna geometria, zwana geometrią euklidesową, opisuje Wszechświat. Naturalną próbą odpowiedzi będzie eksperymentalne sprawdzenie, czy twierdzenia tej geometrii zachodzą w otaczającej nas przestrzeni. Na przykład możemy zbadać, czy suma kątów wewnętrznych trójkąta utworzonego przez punkt na Ziemi i dwa punkty na różnych odległych gwiazdach wynosi 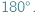 Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
Jednakże wszystkie takie sprawdzenia tego i innych twierdzeń geometrii euklidesowej możemy wykonać jedynie w pewnym otoczeniu Ziemi, którego promień jest wyznaczony zasięgiem naszych teleskopów...
W salonie fryzjerskim siedzi matematyk, obok leży połyskująca para nożyczek, mnóstwo szczotek i innych sprzętów. Matematyk nerwowo wierci się w fotelu - przecież nie od dziś wie, że sfery zaczesać się nie da. Fryzjer intuicyjnie sięga po nożyczki, szalejące nad czołem rozmaitości nie rokują zbyt dobrze. Niechętny rozspójnieniu klient wpada na pomysł - warkocz będzie idealny!
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty