Jak wykryć salamandrę?
Przyjrzyjmy się problemowi, przed którym staje legislator wyborczy: podział kraju na okręgi wyborcze...
Przyjrzyjmy się problemowi, przed którym staje legislator wyborczy: podział kraju na okręgi wyborcze...
Skończyłam! - krzyknęła triumfalnie Agatka do swojego brata, Bartka. Dziewczynka regularnie domaga się od starszego chłopca rozmaitych ciekawostek matematycznych, których ten dowiaduje się w liceum...
Czy można ograć kasyno? Nałogowi gracze zastanawiają się nad tym problemem od dawna. Wszystkie gry w kasynie mają ujemną wartość oczekiwaną dla klienta. Przynajmniej tak się ludziom wydawało aż do lat 60., kiedy ukazało się kilka książek o tym, jak można, stosując odpowiednią strategię, uzyskać dodatnią wartość oczekiwaną w grze Blackjack. To ogromnie spopularyzowało grę i paradoksalnie okazało się korzystne dla branży hazardowej. Mechanizm został przedstawiony w filmie "21", jednak bez żadnych szczegółów. W tym artykule przedstawię dokładniej, jak ta strategia działa.

Photo: Stanford University.
Maryam Mirzakhani (1977-2017)
W matematyce nie przyznaje się Nagrody Nobla, jednakże od ustanowienia w 1936 roku Medalu Fieldsa (od nazwiska kanadyjskiego matematyka Johna Charlesa Fieldsa) wyróżnienie to stało się najważniejszą nagrodą w tym obszarze badań. Fields uczestniczył w jej powstaniu, zaprojektował towarzyszący jej medal i pozostawił funduszowi Medalu Fieldsa kwotę 47000 dolarów kanadyjskich. Finansowy dodatek do Medalu to 15000 dolarów kanadyjskich, znacznie mniej niż 8 milionów szwedzkich koron (około 800000 euro) przyznawanych w ramach Nagrody Nobla, mimo to w oczach matematyków prestiż tego wyróżnienia jest nie mniejszy. Obecnie w matematyce przyznawana jest także Nagroda Abela oraz inne wysoko cenione wyróżnienia, jednak najdłuższa tradycja stoi za Medalem Fieldsa.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W wielu zadaniach, w których występują kąty lub ich sumy, przydatne bywa przeniesienie pewnych figur tak, by kąty te znalazły się obok siebie. Szczególnie wygodne jest to wtedy, gdy suma pewnych kątów równa jest np. 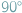 lub
lub 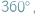 a także, gdy niektóre z danych odcinków są równej długości.
a także, gdy niektóre z danych odcinków są równej długości.

wikipedia
Srinivasa Ramanujan (1887-1920)
Srinivasa Ramanujan Ijengar (1887-1920) był indyjskim matematykiem z prowincji Madras, genialnym samoukiem obdarzonym niezwykłym talentem do odkrywania zaskakujących zależności liczbowych. Swobodnie posługiwał się ułamkami łańcuchowymi, szeregami liczbowymi, funkcjami eliptycznymi. Pozostawił około 3900 wzorów, z których jedynie niewielka część została dotychczas sprawdzona.
Geometrzy od dawna marzyli o współrzędnych jednorodnych, czyli takich  -tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w
-tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w  -tce pomnożymy przez tę samą liczbę, to nowa
-tce pomnożymy przez tę samą liczbę, to nowa 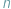 -tka będzie współrzędnymi tego samego punktu.
-tka będzie współrzędnymi tego samego punktu.
Słynne twierdzenie Dirichleta głosi, że jeżeli liczby naturalne 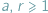 są względnie pierwsze, to ciąg arytmetyczny
są względnie pierwsze, to ciąg arytmetyczny 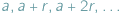 zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
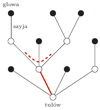
Rys. 1 Przykładowa Hydra.
Drodzy Poszukiwacze Przygód, witam Was na kolejnym szkoleniu. Dzisiaj nauczymy się jak rozpoznawać, znajdować i radzić sobie w boju z Hydrą. Hydry to paskudne stworzenia, zamieszkujące świat grafów. Niech Was nie zmyli rysunek obok. Zobaczcie, jak przerażająco on wygląda. Hydry to bestie, które tylko upodobniają się do drzew, aby Was zmylić! Tam, gdzie niektórzy z Was dostrzegają korzeń, znajduje się tułów bestii. Tam, gdzie wydają się być liście, są głowy naszego stwora. Krawędzie to szyje, a wierzchołki wewnętrzne to zgięcia.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W tym artykule omówimy pewną bardzo pożyteczną technikę - tzw. przesuwanie. Polega ona na tym, że niektóre obiekty przesuwamy o pewien wektor i udowadniamy, że teza zadania jest niezmiennicza ze względu na wykonanie tej operacji. Ta metoda pozwala na sprowadzenie rozwiązywanego zadania do znacznie prostszego. Bardzo często ten prostszy przypadek ma jakiś rodzaj symetrii, z której łatwo wywnioskować tezę. Zanim przejdziemy do rozwiązywania zadań, odnotujmy dwie proste własności opisanej operacji.
Każdy z nas obcował z działaniami pisemnymi na liczbach naturalnych - dodawaniem, odejmowaniem, mnożeniem i dzieleniem. Z pisemnym potęgowaniem można się rozprawić, wielokrotnie stosując pisemne mnożenie. Dzieląc dwie liczby całkowite, możemy otrzymać pełne rozwinięcie dziesiętne (okresowe lub skończone) albo uzyskać dowolną dokładność wyniku. Tak, działania pisemne są sprytne. A co z pierwiastkowaniem? Czy istnieje metoda na pisemne wyznaczanie kolejnych cyfr rozwinięcia dziesiętnego liczby 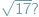 Odpowiedź brzmi: tak.
Odpowiedź brzmi: tak.
W poprzednim numerze przedstawiliśmy cykl wzajemnie wpisanych trójkątów i dwa wzajemnie wpisane pięciokąty. To było na płaszczyźnie. A teraz będzie przykład wzajemnego wpisania w przestrzeni trójwymiarowej.
Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 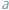 i
i 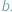 Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach
Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach 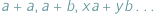 Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów
Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów 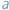 i
i  a niektóre można otrzymać na wiele sposobów.
a niektóre można otrzymać na wiele sposobów.
Proste do zdefiniowania i zrozumienia problemy geometryczne często są trudne do rozwiązania i wymagają użycia skomplikowanych algorytmów. Weźmy, na przykład, zadanie polegające na znalezieniu największego okręgu, który możemy zmieścić w wielokącie. Środek tego okręgu nazywany jest środkiem Czebyszewa. Jeżeli mamy do czynienia z dowolnie wybranym trójkątem bądź wielokątem foremnym, środek Czebyszewa znajduje się w punkcie przecięcia dwusiecznych jego dwóch dowolnych kątów. Zagadnienie staje się o wiele bardziej skomplikowane, gdy weźmiemy pod uwagę dowolny, nieregularny wielokąt.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W wielu grach dla któregoś z graczy istnieje strategia wygrywająca, czyli taka "recepta" na grę, która pozwala zawsze zwyciężyć, niezależnie od ruchów przeciwnika. Jednak strategię taką, nawet jeśli istnieje, nie zawsze łatwo wskazać. Na szczęście często można. Czasem wystarczą do tego proste pomysły typu symetria, czasem zaś potrzebne są metody bardziej wyrafinowane. W niektórych grach nawet bez żadnej strategii wynik jest z góry przesądzony. Ilustrują to poniższe przykłady...
Gry, zagadki, paradoksy Deltoid
Gra Black rozgrywana jest przez dwóch graczy (I - rozpoczynającego i II) na prostokątnej planszy podzielonej na kwadratowe pola jednostkowe; każdy z wymiarów planszy jest większy od 2...
Według niezliczonych źródeł internetowych (w tym polskiej Wikipedii) geometryczny środek Polski znajduje się w miejscowości Piątek. Zastosowana do uzyskania tego wyniku metoda opiera się na wyznaczeniu figury sferycznej złożonej z fragmentów południków i równoleżników przechodzących przez najbardziej wysunięte w czterech kierunkach świata punkty naszego kraju, a następnie wyznaczeniu przecięcia ortodrom (są to "linie proste" na sferze, czyli fragmenty okręgów wielkich) łączących przekątniowo te cztery punkty.

Widoczny obok splot trzech rurek to logo włoskiego rodu Boromeuszy. Splot ten ma interesującą własność: rozcięcie i usunięcie dowolnej z tych rurek sprawia, że pozostałe dwie nie są ze sobą w żaden sposób połączone. W tym miejscu pojawia się naturalne pytanie - czy da się skonstruować splot o podobnej własności dla więcej niż trzech rurek?
Dawno, dawno temu żył sobie beztrosko król wraz ze swoją piękną córką. Jak to czasem w zbyt szczęśliwych królestwach bywa, pewnego razu czarnoksiężnik przybył na dwór, żeby porwać królewnę i uwięzić ją w swojej upiornej wieży. Zgodnie z zasadami dobrego wychowania mrocznych czarodziei, do których należał, musiał dać mieszkańcom królestwa możliwość ocalenia królewny przed swoim niecnym planem...
Tzw. zagadnienie Fermata to pytanie o to, gdzie wewnątrz danego trójkąta 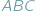 należy umieścić punkt
należy umieścić punkt 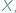 aby suma długości odcinków
aby suma długości odcinków 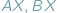 i
i 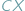 przyjęła najmniejszą wartość.
przyjęła najmniejszą wartość.