Matematyka Klub 44 - Matematyka
Klub 44M - zadania X 2018
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Pierre de Fermat (1601-1665)
Pierre de Fermat był Francuzem i żył w pierwszej połowie XVII wieku (1601-1665). Jako radca prawny praktykował w sądzie w Tuluzie na południu Francji. Naukami ścisłymi, a w szczególności matematyką, interesował się jako amator, ale wniósł potężny wkład do ich rozwoju. Szczególnie spektakularne są jego osiągnięcia w teorii liczb i o nich traktuje niniejszy artykuł. Wszyscy wiedzą, że jest Wielkie Twierdzenie Fermata (WTwF), Małe Twierdzenie Fermata (MTwF) i jeszcze inne twierdzenia Fermata dotyczące teorii liczb - ale które z nich jest największe?
Na wiele problemów matematycznych warto spojrzeć z innej strony (lub z dwóch stron jednocześnie), przeanalizować dualną sytuację, dostrzec alternatywną wersję tego samego zagadnienia...
Kwadrat i koło mają swoje naturalne odpowiedniki trójwymiarowe (sześcian i kula), czterowymiarowe, pięciowymiarowe i dowolnie wymiarowe. Pisząc "dowolny wymiar", mamy na myśli więcej osi układu, czyli też współrzędnych opisujących obiekt. Wyobraźmy sobie mianowicie przestrzeń trójwymiarową (co nie jest specjalnie trudne). Każdy punkt takiej przestrzeni można opisać za pomocą zestawu trzech współrzędnych 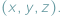 Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych
Gdy opisujemy położenie punktu na płaszczyźnie, myślimy zwykle o układzie kartezjańskim i parze współrzędnych 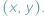 Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej
Opisując punkt na prostej, używamy tylko jednej liczby. Gdy zaś chcemy opisać przestrzeń czterowymiarową, lub ogólniej 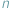 -wymiarową, używamy zestawu
-wymiarową, używamy zestawu 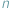 liczb
liczb 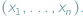
Jeszcze w r. 1908, pisząc o wspólnym brzegu dwu obszarów płaskich (z których jeden jest ograniczony), Schoenf1ies uważał, że można ten brzeg rozłożyć na dwa luki krzywe (przez luk krzywy rozumiał w tym przypadku kontinuum nie rozcinające płaszczyzny lub, co na jedno tu wychodzi, kontinuum rożne od całego brzegu). Był to błąd, który sprostował Brouwer w pracy Źur Analysis SitlIs"(Mathematische Annalen 68 (1910),422-434)...
Tym razem o własności punktu stałego...

Jakie jest maksymalne pole sofy, którą można przesunąć przez korytarz w kształcie litery L o jednostkowej szerokości? - taki problem sformułował ponad 50 lat temu austriacko-kanadyjski matematyk Leo Moser.
Spójrzmy na poniższe obrazki i nie zastanawiając się, co właściwie przedstawiają, spróbujmy zgadnąć, jak powinien wyglądać kolejny.
Uczciwi złodzieje powinni umieć się dzielić. Oczywiście, dzielić się łupami z innymi uczciwymi złodziejami, którzy pomagali w dokonaniu kradzieży. Można sobie wyobrazić, że taka uczciwość powoduje czasem pewne trudności, gdyż niektóre precjoza mogą być nieskore do podziału. Dla przykładu...
Problem szyfrowania przesyłanych wiadomości sięga jeszcze czasów starożytnych, więc naszego nowego deltowego cyklu artykułów o kryptologii prezentowanego w rubryce "A jednak się da!" nie możemy nie zacząć od przypomnienia najstarszego znanego systemu szyfrowania, mianowicie szyfru Cezara. Szyfr ten nie jest specjalnie wyrafinowany...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
Zasada szufladkowa Dirichleta głosi, iż jeśli rozmieszczamy pewną liczbę obiektów w mniejszej liczbie szufladek, to któreś dwa z nich trafią do tej samej szufladki. Podobnie, jeśli liczba obiektów jest większa niż dwukrotność liczby szufladek, któreś trzy trafią razem do szufladki itd.
W 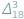 (Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
(Z notatnika geniusza) i w tym numerze (Zagnieżdżone pierwiastki) przedstawione są różne zależności liczbowe pochodzące od Ramanujana. Robią ogromne wrażenie, tym bardziej że Ramanujan podał je bez uzasadnień i dla nas mają status natchnionej wizji...
Zupełnie nieszokująca zasada dobrego uporządkowania mówi, że każdy niepusty podzbiór liczb naturalnych ma element najmniejszy. Pokażemy, jak ją wykorzystać do wykazania, że 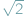 jest niewymierne, czyli że dla żadnej liczby naturalnej
jest niewymierne, czyli że dla żadnej liczby naturalnej 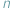 liczba
liczba 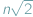 nie jest całkowita.
nie jest całkowita.
W 1911 roku Srinivasa Ramanujan 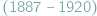 zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a)
zaproponował czytelnikom Journal of the Indian Mathematical Society (JIMS 3 (1911), Question 289, p. 90) wyznaczenie wartości: (a) 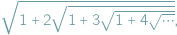 (b)
(b)  Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.
Ponieważ pytania te w 1911 r. nie doczekały się odpowiedzi, więc Ramanujan podał je w kolejnym tomie JIMS 4 (1912), p. 226. Zadania Ramanujana można rozwiązać prosto i elegancko.
Jaka jest liczba różnych 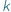 -elementowych podzbiorów zbioru
-elementowych podzbiorów zbioru 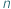 -elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez
-elementowego? Jest to jedno z pierwszych pytań, które zadajemy sobie, zaczynając zajmować się elementarną kombinatoryką. Wkrótce dowiadujemy się, że liczbę tę oznacza się przez 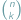 (symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
(symbol Newtona), a następnie poznajemy różne metody jej wyznaczania. Wyjściowe pytanie o liczbę podzbiorów przeniesiemy na nieco wyższy poziom abstrakcji, zmieniając w nim kilka pojęć...
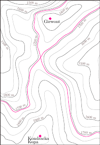
Typowe (regularne) poziomice zaznaczone są na szaro, a nietypowe (osobliwe) na kolorowo.
Mapa obok przedstawia rejon Giewontu i Kopy Kondrackiej. Typowa poziomica jest albo pusta (np. nie ma żadnych punktów na wysokości 2500 m), albo składa się z jednej lub więcej składowych, z których każda jest albo zamkniętą pętlą (jak ta wokół Giewontu, 1800 m), albo krzywą o dwóch końcach na brzegu mapy (np. te powyżej dolin Małej Łąki i Kondratowej, 1600 m). Może się jednak zdarzyć, że poziomica jest osobliwa - na wysokości 1894 m mamy izolowany punkt (szczyt Giewontu), a na 1725 m przecięcie w kształcie litery X (Kondracka Przełęcz). Są to jednak pojedyncze przypadki - jak szczyt, przełęcz albo dno kotła - a wszystkie pozostałe poziomice są regularne.

Chaim Zelig Słonimski (1810-1904)
Przy dzieleniu liczb wielocyfrowych metodą pisemną często wykonuje się następującą operację...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W dniach 14-17 czerwca odbył się w Szczyrku XXXV Ogólnopolski Sejmik Matematyków. Jak co roku, Sejmik został zorganizowany przez Pracownię Matematyki i Informatyki Pałacu Młodzieży w Katowicach we współpracy z Uniwersytetem Śląskim; www.spinor.edu.pl
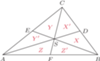
Punkty D, E, F to środki boków, X, X', Y, Y', Z, Z' oznaczają pola.
Środkowa trójkąta to odcinek łączący wierzchołek ze środkiem przeciwległego boku. Środkowe przecinają się w jednym punkcie, zwanym środkiem ciężkości i dzieli on każdą z nich w stosunku 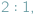 licząc od wierzchołka trójkąta (rys. obok).
licząc od wierzchołka trójkąta (rys. obok).

Najdłużej badanym problemem matematycznym była kwadratura koła. Zaraz za nią uplasowała się kwestia piątego postulatu Euklidesa. Chodziło o to, czy zdanie "jeśli dwie proste przecięte trzecią tworzą kąty wewnętrzne jednostronne o sumie mniejszej od dwóch kątów prostych, to proste te po przedłużeniu przetną się i to właśnie z tej strony" spełnia wymagane dla postulatów warunki, czyli czy wyraża rzeczy jasne i oczywiste i czy jest dostatecznie zwięzłe, by być uznane za pierwotną prawdę. Debatę zapoczątkował w V wieku Proklos, odpowiadając dwukrotnie nie i proponując, by wykazać, że usunięcie tego postulatu gmachu geometrii nie naruszy.
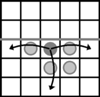
Rys. 1 Możliwe ruchy ciemnoszarego pionka
Conway's Soldiers to jednoosobowa łamigłówka, w której żołnierze (pionki) przedostają się na terytorium wroga i chcą wkroczyć jak najdalej. Na nieskończonej szachownicy, z zaznaczoną "na środku" poziomą granicą, pionki przeskakują jeden nad drugim. Dokładniej: ruch polega na przeskoczeniu pionkiem nad innym znajdującym się na sąsiadującym polu - tylko poziomo lub pionowo - i zdjęciu pionka, który został przeskoczony.
Tak zwana "kryptografia krzywych eliptycznych" to bardzo modne i popularne pojęcie, które rzeczywiście jest ważne, ale - niestety - o którym mówi się najczęściej niezwykle powierzchownie, bez wchodzenia w "detale matematyczne". Niniejszy artykuł próbuje pójść takiemu podejściu pod prąd - chcemy w elementarny sposób objaśnić, o co tak naprawdę chodzi z tymi krzywymi eliptycznymi.