O cyfrowej gotówce (ASJD VI)
Za co kochamy gotówkę? Chyba przede wszystkim za anonimowość transakcji. To znaczy: jeśli Aldona oraz Celina podejmą z banku po banknocie stuzłotowym; następnie Aldona wyda te pieniądze w sklepiku Bogumiła, a Celina u Dobromira; po czym zarówno Bogumił, jak i Dobromir zdeponują zarobione pieniądze z powrotem w banku, to oczywiście bank w żaden sposób nie będzie w stanie stwierdzić, czy klientką Bogumiła była Aldona, czy też może Celina.

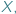 np.
np. 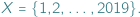 Niech
Niech 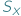 oznacza zbiór funkcji odwracalnych z
oznacza zbiór funkcji odwracalnych z 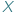 w
w  Funkcje z
Funkcje z 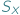 można składać i odwracać, nie wychodząc poza
można składać i odwracać, nie wychodząc poza 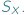 W zbiorze
W zbiorze 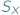 istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru
istnieje też funkcja identycznościowa. Tytułowe grupy są abstrakcyjnym sposobem wyrażenia powyższych własności zbioru 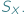
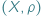 jest przestrzenią metryczną, czyli zbiorem
jest przestrzenią metryczną, czyli zbiorem 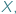 w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.
w którym możemy mierzyć odległość między punktami tego zbioru. W przestrzeni metrycznej możemy zdefiniować pojęcie zbioru otwartego i domkniętego. Zacznijmy od przykładu podzbiorów płaszczyzny ze zwykłą, szkolną metryką euklidesową.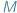 ) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez
) przypiszemy odległość, zwaną także metryką (oznaczamy ją przez 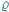 ), to powstanie przestrzeń metryczna
), to powstanie przestrzeń metryczna 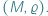
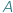 i
i 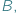 relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru
relacją zdefiniowaną pomiędzy tymi dwoma zbiorami matematycy nazywają po prostu podzbiór zbioru wszystkich par elementów, w których pierwszy jest ze zbioru 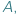 a drugi ze zbioru
a drugi ze zbioru 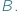 Inaczej mówiąc, element ze zbioru
Inaczej mówiąc, element ze zbioru 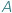 i element ze zbioru
i element ze zbioru 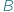 mogą być w danej relacji lub w niej nie być.
mogą być w danej relacji lub w niej nie być.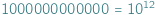 mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.
mieści się aż milion milionów, mało kto jest w stanie to sobie wyobrazić. Wszystkie te liczby wpadają w tę samą kategorię - liczb dużych na tyle, że nie znajdujemy dla nich zastosowania w zwyczajnym codziennym życiu.