Delta mi!

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Najbardziej królewskie części trójkąta i ich własności.

W trakcie lektury artykułu Piotra Chrząstowskiego-Wachtela o uogólnieniach (Delta 2/2020) przypomniałem sobie o kilku innych problemach matematycznych, które podlegają opisanej tam zasadzie. Przypomnę - problem postawiony w pewnym szczególnym przypadku może okazać się trudniejszy do udowodnienia niż problem ogólny. Z drugiej strony wiem, że czasami rozwiązanie przypadku szczególnego daje gotowe rozwiązanie przypadku ogólnego. Chciałbym przybliżyć Czytelnikowi kilka innych przykładów takiego postępowania, które poznałem w trakcie studiów oraz podczas wędrówki po ciekawych problemach matematycznych.

W marcu 1672 roku do Paryża przybył z misją dyplomatyczną od elektora mogunckiego młody prawnik, filozof i erudyta Gottfried Wilhelm Leibniz (1646-1716). Spotkanie z Christiaanem Huygensem (jesienią 1672 r.) przekonało Leibniza, że w matematyce jest nowicjuszem. Huygens, chcąc zbadać matematyczną przenikliwość Leibniza, rzucił mu takie oto wyzwanie: wyznaczyć sumę szeregu 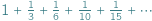Leibniz zadanie wykonał (a Ty? rozwiązanie jest tutaj)...

Zgodnie ze starożytnym żydowskim prawem, jeśli oskarżony w wyniku procesu przed Sanhedrynem został jednogłośnie uznany za winnego zarzucanych mu czynów, to odstępuje się od wymierzenia kary! Taka zasada dla wielu Czytelników jest zapewne szokująca. Jednak ówcześni twórcy prawa uznawali, że jednomyślność sędziów często wskazuje na niedopatrzenie przy ocenie dowodów winy. To mogło wypaczyć wynik procesu...

Jak dobrze wiemy, żyjemy w wyjątkowym okresie w dziejach, w którym dostęp do informacji jest niesłychanie łatwy, i w zasadzie z roku na rok ułatwienia w tym zakresie zwiększają się. Z pewnością tym bardziej zwiększą się one w bieżącym roku - 2020. Podobnie jest z ilością danych, zbieramy ich coraz więcej. Gromadzimy olbrzymie ilości zdjęć, muzyki, filmów, ale również i innych danych, takich jak teksty, wszelkiego rodzaju informacje o ruchu w sieci itd. Przykładowo w ciągu każdej minuty na serwis YouTube wrzucanych jest około 500 godzin filmów. Powstała nawet dziedzina badań zajmująca się analizą dużych danych, zwana z angielska Big Data...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Jak co miesiąc, trzy ciekawe zadania z matematyki...

Piramidy w starożytnym Egipcie budowano na kształt ostrosłupa prawidłowego o podstawie kwadratu. Jak pokazują źródła historyczne, starożytni Egipcjanie potrafili obliczyć objętość takiego ostrosłupa. Jednak ich dobrze rozwinięta, jak na tamte czasy, matematyka, miała głównie zastosowanie praktyczne i raczej nikt nie formułował pytań, które miałyby na celu jedynie matematyczną rozrywkę. Jednym z matematyków, który szczególnie interesował się rozrywkowymi zastosowaniami królowej nauk, był Édouard Lucas, autor między innymi słynnej gry zwanej Wieżą Hanoi. W niniejszym artykule zwrócimy uwagę na sformułowany przez Lucasa problem z gatunku tych raczej mało praktycznych. Jak zobaczymy, ma on pewien związek z piramidami.

Czy istnieje coś takiego jak matematyka eksperymentalna? Zobaczmy. Ten tekst zaczniemy od prostego zadania z geometrii, następnie użyjemy komputera, aby rozwiązać je w przybliżeniu, a na koniec z tego przybliżenia zgadniemy dokładny wynik. Będzie też wiele szczegółów do uzupełnienia dla Czytelników. Programy użyte do eksperymentów można znaleźć w [3].

O półniezmiennikach, dzięki którym wykazujemy, że pewne przekształcenia można wykonać tylko skończenie wiele razy.

W pierwszej części artykułu (Delta 7/2020) omówiliśmy pojęcia funkcji logicznej, jej czułości i przedstawiliśmy, na razie bez dowodów, pewne związane z nimi twierdzenia, udowodnione w pracy [1]. Celem drugiej części jest przedstawienie owych dowodów w wersji nieco uproszczonej w stosunku do oryginalnej pracy [1], ale wciąż wymagającej znajomości podstaw algebry liniowej, w tym mnożenia macierzy i pewnej wiedzy o wymiarze przestrzeni liniowej.

W stosunku do wielkości Ziemi wszystkie ziemskie nierówności (łańcuchy górskie, doliny) to znikome, zaniedbywalne zniekształcenia. Ponieważ w naszej skali nasze bliskie otoczenie przypomina płaską powierzchnię, więc nie powinno nas dziwić, że pierwsze geometryczne rozważania dotyczyły płaszczyzny.

W matematyce często rozróżnia się rzeczy liniowe od nieliniowych. W szkole uczy się o funkcjach liniowych i nieliniowych, ale te pojęcia są dużo szersze i oprócz teorii dotyczą także wielu sytuacji praktycznych. Układ liniowy można przeanalizować w ten sposób, że rozkłada się go na części, analizuje działanie każdej z nich osobno, a na końcu dodaje do siebie poszczególne wyniki. W układzie nieliniowym taka analiza może dać niepoprawne wyniki.

W 1918 roku George Pólya opublikował artykuł Zahlentheoretisches und wahrscheinlichkeits-theoretisches über die Sichtweite im Walde, w którym rozważał następujący problem (w literaturze anglojęzycznej nosi on nazwę Orchard Visibility Problem).

W poprzednim artykule (Delta 7/2020) pokazaliśmy, czym są interwały naturalne (wynikające z szeregu alikwotowego) oraz to, że przy użyciu do strojenia instrumentu tylko oktaw i kwint czystych "koło się nie zamknie". W pewnym momencie zaczęło to sprawiać problem - odkąd pojawiła się w muzyce europejskiej muzyka wielogłosowa i operowanie trójdźwiękiem. Czysty trójdźwięk durowy (jak go obecnie nazywamy) składa się oczywiście z trzech dźwięków...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Jak co miesiąc, trzy ciekawe zadania z matematyki...

W mieście Parzystkowo zacny burmistrz postanowił w nietypowy sposób zaktywizować społeczeństwo. Zarządził utworzenie stowarzyszeń, które wykonywać będą powierzone im zadania...

Tytułowe twierdzenie sformułujemy dla trójkąta (z brzegiem) na płaszczyźnie euklidesowej 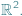Jest to najsłynniejsze i najważniejsze twierdzenie w topologicznej teorii punktów stałych o rozlicznych zastosowaniach (w równaniach różniczkowych, topologii, ekonomii, teorii gier, analizie funkcjonalnej). Jego odkrycie miało ogromny wpływ na rozwój wielu gałęzi matematyki, szczególnie topologii algebraicznej.

Najpierw jednak spróbujmy wyjaśnić, dlaczego poważni specjaliści chcieli w ogóle rozważać tak (pozornie) niepoważne zagadnienie...

Standardowym postępowaniem jest ujednorodnianie dowodzonych nierówności za pomocą danego w zadaniu warunku. Ciekawiej jest na odwrót - gdy mamy udowodnić jednorodną nierówność, możemy często założyć coś dodatkowo o występującej w niej zmiennych. Naprawdę!

Jak przekazują nam starożytni, zaczęło się od przypadkowego odkrycia przypisywanego Pitagorasowi - otóż miał on spostrzec, że jeśli stosunek długości dwóch strun jest równy stosunkowi dwóch małych liczb naturalnych, to współbrzmią one harmonijnie...

W naszych czasach coraz więcej rzeczy staje się tajnych. To dlatego, że nasze życie jest coraz bardziej uzależnione od setek i tysięcy drobiazgów, a kontrolę nad nimi każdy chce zachować dla siebie. Przyjdzie może czas, kiedy na posiadanie tablic logarytmicznych wymagane będzie zezwolenie. Żarty? Mam nadzieję. Na razie grozi nam utajnienie tablic rozkładów liczb na czynniki pierwsze. A oto dlaczego...

O telefonicznej czy korespondencyjnej grze w szachy słyszał każdy. Ale jak grać w ten sposób w brydża lub w pokera? Problemem jest oczywiście rozdawanie kart...