Dwusieczne
Skoro dwusieczna to półprosta dzieląca kąt na dwa równe kąty, to dlaczego dwusieczne kątów wewnętrznych każdego trójkąta przecinają się w jednym punkcie? Otóż...
Skoro dwusieczna to półprosta dzieląca kąt na dwa równe kąty, to dlaczego dwusieczne kątów wewnętrznych każdego trójkąta przecinają się w jednym punkcie? Otóż...

W matematycznym świecie od zawsze znajdowało się mnóstwo tajemnic czekających na odkrycie. Tak zawiłych i zdradzieckich, że tylko szaleńcy mogli w ogóle wyobrazić sobie ich istnienie. Tymi szaleńcami byli nieustraszeni matematycy, którzy już od stuleci (jeżeli nie tysiącleci) szukają, rozwiązują i wyjaśniają zagadki, które większość ludzi już dawno uznawała za beznadziejne przypadki (lub są one tak abstrakcyjne, że w żaden sposób nieosiągalne).
Rachunek prawdopodobieństwa Drobiazgi
Kostką dyskretną wymiaru 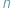 nazywamy
nazywamy 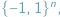 czyli zbiór wierzchołków kostki
czyli zbiór wierzchołków kostki ![n [−1;1] ;](/math/temat/matematyka/analiza/2016/03/22/Analiza_na_kostce_dyskretnej/3x-f82bbe1071526c4148f9cb4c0db2ef3cf785b199-im-65,9A,A1-FF,FF,FF.gif) stanowiącej
stanowiącej 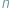 -wymiarowy odpowiednik sześcianu...
-wymiarowy odpowiednik sześcianu...
Najogólniej mówiąc, kombinatoryka ekstremalna zajmuje się pytaniami o to, jaki jest rozmiar największego (lub najmniejszego) możliwego zbioru obiektów danego typu, spełniającego pewien zadany warunek i jak takie ekstremalne przypadki wyglądają.
Pozwolę sobie podtrzymać Czytelnika w napięciu i tytułowe pytanie tymczasem zostawię bez odpowiedzi. Zacznę za to od refleksji, czym jest płaskość.
Większość osób świadomych powiązań między światem matematyki a rzeczywistością zgodzi się, że na każdym kroku spotykamy się z rachunkiem prawdopodobieństwa. Oprócz niektórym dobrze znanych zagadnień związanych z grami losowymi pewne prawidłowości probabilistyczne możemy spotkać również w bardziej niespodziewanych miejscach.
Rozważmy następujący problem: gromadzimy powierzchnie wszystkich krajów wyrażone w kilometrach kwadratowych i patrzymy tylko na pierwsze cyfry znaczące tych wartości. Otrzymamy listę liczb z zakresu od 1 do 9 włącznie; pytanie brzmi, jakie są częstości ich występowania w tym zbiorze?
Zastosowania matematyki Epidemie
Prawie co roku w sezonie grypowym w mediach pojawia się temat szczepień. Omawiane są różne aspekty, podawane argumenty za i przeciw szczepieniom, często obserwujemy więcej emocji niż racjonalizmu. Epidemie, a w szczególności pandemie, stanowią przedmiot badań od wielu lat ze względu na swój znaczący wpływ na rozwój populacji ludzkiej. Zarówno w starożytności, jak i w średniowieczu, a także już w czasach współczesnych różnego typu choroby, takie jak dżuma, tyfus, cholera, grypa, dziesiątkowały mieszkańców naszego globu.
Grupa warkoczy była rozważana po raz pierwszy przez Adolfa Hurwitza w roku 1885, jednak nie pod tą nazwą; w grupie rozważanej przez Hurwitza trudno było dopatrzyć się warkoczy. Nazwę wprowadził Emil Artin w roku 1925, bo w jego interpretacji elementy grupy kojarzą się z warkoczami. Przypomnę, jak się je zaplata...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Oznaczmy przez 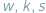 liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem
liczby odpowiednio wierzchołków, krawędzi i ścian wielościanu. W każdym wierzchołku schodzą się co najmniej trzy końce krawędzi i każda krawędź ma dwa końce, zatem 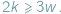 Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc
Podobnie każda ściana ma co najmniej trzy boki, a każda krawędź należy do dwóch ścian, więc 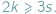 Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera:
Ponadto jeśli wielościan jest wypukły, zachodzi wzór Eulera: 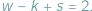
Rachunek prawdopodobieństwa Drobiazgi
W teorii prawdopodobieństwa mówimy o modelu klasycznym, gdy zbiór wszystkich zdarzeń elementarnych 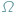 jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...
jest zbiorem skończonym i wszystkie zdarzenia jednoelementowe są jednakowo prawdopodobne...
Dotarliśmy do ostatniej części cyklu, w którym prezentujemy wybrane przykłady zaskakujących relacji pomiędzy różnymi, pozornie bardzo odległymi, obszarami matematyki. Nie wypada jednak zakończyć bez poświęcenia należytej uwagi dziedzinie teorii liczb. Jak bowiem matematyka nazywana jest często królową nauk, tak o teorii liczb mówi się często jako o królowej matematyki. A królowa ma, oczywiście, wielu służących.
Chociaż są to pojęcia abstrakcyjne (bo przecież nikt nie widział ani punktu, ani odcinka), przemawiają dobrze do wyobraźni i zgadzają się ze zdrowym rozsądkiem. I aż dziw bierze, jak wiele wokół nas zjawisk, które zdają się ostrzegać: uwaga to co wydaje się takie oczywiste, wcale nie musi być prawdziwe.
Jednym z podstawowych wzorów trygonometrycznych jest twierdzenie kosinusów podające zależność między bokami trójkąta a jednym z jego kątów: 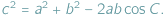 Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt
Na formułę tę można patrzeć jako na uogólnienie twierdzenia Pitagorasa (do którego sprowadza się, gdy kąt 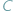 jest prosty, czyli
jest prosty, czyli 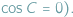
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
- Z tymi ułamkami to zupełnie nic nie wiadomo - narzekał po lekcji matematyki Janek. - Na przyklad 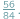

wikipedia
Alfred Tarski (1901-1983)
W artykule tym pragnę omówić pewne pojęcia, należące całkowicie do zakresu geometrii elementarnej, a dotąd niemal wcale nie zbadane. Jak wiadomo, dwa wielokąty 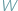 i
i 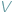 nazywamy równoważnymi, wyrażając to wzorem:
nazywamy równoważnymi, wyrażając to wzorem: 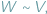 jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...
jezeli dają się one podzielić na jednakową ilość wielokątów odpowiednio przystających...
Symbol Newtona 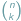 dla liczb całkowitych
dla liczb całkowitych 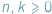 oznacza liczbę sposobów wybrania zbioru
oznacza liczbę sposobów wybrania zbioru 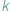 elementów spośród
elementów spośród 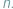 W szczególności
W szczególności 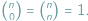
Rozważamy wielomian 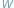 o współczynnikach rzeczywistych stopnia
o współczynnikach rzeczywistych stopnia 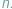 Wiadomo, że wielomian taki ma
Wiadomo, że wielomian taki ma 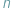 pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu
pierwiastków zespolonych; niektóre z nich (czasami wszystkie) są, być może, rzeczywiste. Twierdzenie Sturma pozwala obliczyć liczbę pierwiastków rzeczywistych wielomianu 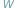 należących do wybranego przedziału
należących do wybranego przedziału 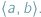 Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej
Oczywiście, odpowiedź na to pytanie możemy uzyskać, stosując metodę badania funkcji wielomianowej 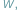 znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
znaną z analizy matematycznej. Metoda Sturma jest czysto algebraiczna, nie stosuje metod analizy matematycznej.
Znana łamigłówka wieże Hanoi ma następujące reguły...

Gwoli precyzji ustalmy, że trzymając przed sobą zetknięte połówki przeciętej bryły obrotowej (prawą i lewą), obracamy prawą z nich ruchem do siebie.
Taka sobie niewinnie wyglądająca bryłka. Ot, powstała z obrotu kwadratu dookoła jego przekątnej, przecięcia tego, co powstało, na dwie identyczne części (wzdłuż płaszczyzny kwadratu), przekręceniu połowy o 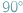 i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
i doklejeniu do drugiej części (czekającej w tym czasie w bezruchu). Szczęśliwa całość - sferostożek (ang. sphericon).
Rachunek prawdopodobieństwa Drobiazgi
Są trzy symetryczne monety...
Niedługo po ukazaniu się mojego artykułu Kolorowe czapeczki do redakcji przyszedł list od wieloletniego Czytelnika Delty, Jana Błaszczyńskiego, z propozycją rozwiązania postawionego tam problemu. Proste rozwiązanie Jana Błaszczyńskiego, w przeciwieństwie do przedstawionego w moim artykule, jest deterministyczne  i na dodatek pozwala rozstrzygnąć problem dla dowolnej liczby kolorów czapeczek i dowolnej liczby krasnoludków.
i na dodatek pozwala rozstrzygnąć problem dla dowolnej liczby kolorów czapeczek i dowolnej liczby krasnoludków.