Matematyka Klub 44 - Matematyka
Klub 44M - zadania X 2011
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Stereometria Kącik przestrzenny
W tym odcinku przyjrzymy się kątom dwuściennym. Jedną z najbardziej skutecznych metod radzenia sobie z nimi jest przeformułowanie problemu tak, żeby zamiast kątów dwuściennych pojawiły się kąty płaskie.

Gdy poznajemy matematykę, liczby oznaczane symbolami
 oraz
oraz
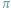 pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
pojawiają się bardzo często. Uznając ważność tych liczb, badamy ich arytmetyczną
naturę. Wiemy, że
 jest liczbą niewymierną (L. Euler, 1737 r.) oraz
jest liczbą niewymierną (L. Euler, 1737 r.) oraz
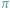 jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
jest
liczbą niewymierną (J.H. Lambert, 1767 r.). Przestępność liczby
 wykazał
Ch. Hermite w 1873 r., a przestępność liczby
wykazał
Ch. Hermite w 1873 r., a przestępność liczby
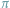 wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
wykazał w 1882 r.
F. Lindemann. Wyznaczenie dobrych przybliżeń wartości tych liczb nie jest
zadaniem banalnym. Przypomnijmy, jak można to zrobić.
Zdarza się czasem, że zachód słońca i pusta, piaszczysta plaża zachwycają nas, kiedy patrzymy na nie, spacerując brzegiem morza, jednak zamknięte w martwe ramy zdjęcia przywodzą na myśl co najwyżej słowo „kicz”. Ta historia, gdyby jeden z hollyłódzkich reżyserów zdecydował się nakręcić film na jej podstawie, wydałaby się z pewnością banalna. Tymczasem napisało ją życie.
Zadania konkursowe zawodów stopnia pierwszego.
Zawody stopnia pierwszego 1 września 2011 r. – 24 października 2011 r.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W poprzednim deltoidzie zaprezentowano kilka zadań z geometrii płaskiej, rozwiązanych poprzez „wyjście w przestrzeń”. Oto garść kolejnych przykładów na to, że warto płaskie rysunki postrzegać jako ilustracje sytuacji trójwymiarowych.
Trzy kółeczka łatwo ułożyć w trójkąt foremny (czyli równoboczny), cztery w czworokąt foremny (czyli kwadrat), pięć w pięciokąt foremny itd. Można więc 3 uważać za liczbę trójkątną, cztery za czworokątną, pięć za pięciokątną itd. Rysunki poniżej pokazują, jak można, rysując kropki, określić inne liczby wielokątne.
Niektóre zadania z geometrii płaskiej łatwiej najpierw rozwiązać w przestrzeni, a później dopiero z powrotem je „spłaszczyć”. Liczne przykłady pojawiły się w deltoidach 17 i 18. Oto jeszcze dwa tego rodzaju problemy.
Planimetria Stowarzyszenie na rzecz Edukacji Matematycznej
W grudniu 2010 roku ukazał się drugi tom serii wydawniczej Biblioteczka Stowarzyszenia na rzecz Edukacji Matematycznej zatytułowany Matematyka. Poszukuję – odkrywam. Materiały w nim zawarte stanowią opracowania referatów wygłoszonych w ramach konferencji Konkursy matematyczne w Polsce, zorganizowanej w 2008 roku przez Uniwersytet Warszawski we współpracy ze Stowarzyszeniem na rzecz Edukacji Matematycznej.
Myślę, że niemal każdy Czytelnik miał okazję się z nią spotkać. Załóżmy, że
mamy dany trójkąt, i wybierzmy dowolny punkt
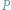 z okręgu na nim opisanego.
Wówczas rzuty prostokątne punktu
z okręgu na nim opisanego.
Wówczas rzuty prostokątne punktu
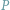 na proste zawierające boki danego
trójkąta leżą na jednej prostej zwanej prostą Simsona.
na proste zawierające boki danego
trójkąta leżą na jednej prostej zwanej prostą Simsona.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Kiedy po ustawowych zaostrzeniach wprowadzono surowy nakaz Kaganiec noś i przy pogodzie, rozdrażniony pieski świat wyległ na ulice. Choć jazgot był straszliwy, spontaniczna demonstracja pod hasłem Pieska ich niebieska odbywała się pokojowo i nikt nikogo nie ugryzł.
Arytmetyka szkieletowa (ang. skeleton arithmetic, skeletons, arithmetical restorations) to dział matematyki rekreacyjnej, obejmujący zadania, które polegają na odtwarzaniu pełnego zapisu działania arytmetycznego na podstawie jego „szczątków”.
Zadanie z pieskiem, które zapowiadało w lipcu ten numer Delty, w nieco prostszej wersji (podstawa 10) opublikowałem w Rewii Rozrywki, nr 247 (10/2007). Pozostałe trzy, podane niżej, nie mają rozwiązania w systemie dziesiętnym i dotąd ich nie publikowałem.
Język polski nie jest zbyt przyjazny autorom alfametyków podwójnie prawdziwych. Mimo to w dziedzinie liczebników złożonych udało mi się skonstruować trochę spektakularnych zadań tej klasy. W języku polskim (podobnie jak w angielskim, a w przeciwieństwie do np. niemieckiego) liczebniki złożone pisze się oddzielnie.
Pierwsza tradycyjna (czyli „słowna”) krzyżówka (crossword, mots croisés, Kreuzworträtsel) ukazała się 21 grudnia 1913 roku w czasopiśmie The New York World, lecz dopiero w roku 1924 (po opublikowaniu przez Simona i Schustera książki z 50 łamigłówkami tego typu) wybuchła prawdziwa „krzyżówkomania”.
Gry, zagadki, paradoksy Drobiazgi
Alfametycznych kwadratów poszukuję od ponad trzydziestu lat. Tylko dwa z nich dotąd opublikowałem (p. poniżej). Oba przykłady kwadratów słów trzyliterowych są ilustracją tzw. liczb automorficznych.
Większość materiału zawartego w tym artykule wykorzystałem wcześniej w moim opracowaniu „Alfametyki, czyli kryptarytmy z sensem”, który powstał dzięki inspiracji redaktora naczelnego Rozrywki, Romana Nowoszewskiego, i ukazał się w latach 2006/2007 w czasopiśmie Rozrywka dla każdego (2006 nr 1 i 2, 2007 nr 6). Artykuł niniejszy jest jego zmienioną i uaktualnioną wersją.
Recreational mathematics is an umbrella term, referring to mathematical puzzles and mathematical games. Not all problems in this field require a knowledge of advanced mathematics, and thus, recreational mathematics often attracts the curiosity of non-mathematicians, and inspires their further study of mathematics.
Wikipedia
Planimetria Stowarzyszenie na rzecz Edukacji Matematycznej
13 i 14 kwietnia odbyły się zawody finałowe LXII OLimpiady Matematycznej. Każdego dnia zawodów 139 uczniów z całej Polski, przez trzysta minut, rozwiązywało trzy zadania. Wszystkie bezbłędnie rozwiązał Filip Borowiec z Kielc, a Maciej Dulęba z Wrocławia i Damian Orlef z Zabrza rozwiązali po pięć i pół.