Analiza, Dedekind i Cantor
Sztuka w trzech aktach z prologiem i epilogiem...
Sztuka w trzech aktach z prologiem i epilogiem...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Wiele wzorów na sumy kolejnych liczb naturalnych, ich kwadratów, sześcianów itp. można uzasadnić (lub przynajmniej przekonująco zilustrować) na rysunkach. Często rysunki te wymagają niewiele lub nawet zero komentarza – są to tzw. dowody bez słów...
W naszych rozważaniach wzbogacimy płaszczyznę o dodatkowy punkt, który
oznaczymy przez
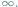 Przyjmiemy przy tym, że ów punkt leży na każdej
z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą
bloków...
Przyjmiemy przy tym, że ów punkt leży na każdej
z prostych. Takie rozszerzone proste oraz okręgi obejmiemy wspólną nazwą
bloków...
Niektórzy sądzą, że geometria jest trudna. Oto zadanie, które wielu by odstraszyło...

Wśród wielu typów zagadnień matematycznych bardzo sobie cenię takie, które po wierzchu są elementarne, łatwe na początku i dające się rozwiązać nietypowymi, efektownymi, niecodziennymi metodami. Dobrze jest też, gdy zadania te są wierzchołkiem pewnej góry lodowej, albo – stosując inne porównanie – są początkiem ścieżki wiodącej nas w nieznane.
Starożytni Egipcjanie sprzed 4000 lat uznawali tylko ułamki proste, czyli takie, które w liczniku miały jedynkę. Oczywiście, były też inne ułamki, ale o nich uczeni mówić nie chcieli – przedstawiali je jako sumę ułamków prostych. Nie byłoby w tym niczego nadzwyczajnego, gdyby nie pretensjonalne wymaganie, aby w owej sumie każdy ułamek był inny.
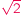 i jeszcze większe niemożliwości
i jeszcze większe niemożliwościPunktem wyjścia niech będzie najsłynniejsza chyba matematyczna konstatacja, ta
mianowicie, że liczba
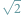 jest niewymierna...
jest niewymierna...

Wikipedia
Rozeta z kościoła St-Jean-de-Malte w Aix-en-Provence
Jednym z najbardziej charakterystycznych elementów architektury średniowiecznej, zwłaszcza gotyckiej, są rozety. Są to okrągłe okna z delikatną konstrukcją kamienną, których puste przestrzenie są najczęściej wypełnione witrażami. Pierwsze rozety pojawiają się już w kościołach romańskich; zamiast witrażami są wypełnione cienkimi płytkami kamiennymi, przepuszczającymi światło.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W zawodach stopnia pierwszego wzięło udział 13288 uczniów z 1089 szkół, do zawodów stopnia drugiego zakwalifikowano 1421 uczniów z 591 szkół, a do zawodów stopnia trzeciego -259 uczniów ze 138 szkół.

W zawodach stopnia pierwszego wzięło udział 1167 uczniów, do zawodów stopnia drugiego zakwalifikowano 507 uczniów, a do zawodów stopnia trzeciego -138 uczniów.
Pewnie część czytelników Delty zna grę Nim – zarówno jej zasady, jak i właściwą dla niej strategię wygrywającą. W tym artykule chcemy przedstawić inną grę grafową. Grę o prostych zasadach, ale trudniejszą niż Nim do dokładnego przeanalizowania. Tą grą jest – stworzony przez Jamie Peabody i Karen Willis – Grim. Podamy efektywny sposób orzekania, który gracz ma strategię wygrywającą. Co najciekawsze, można go zastosować do szerokiej klasy tego typu gier dwuosobowych, zawierającej Grima i Nima.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
W pierwszej części artykułu szukaliśmy prawdopodobieństwa tego, że umierający człowiek będzie starszy od wszystkich aktualnie żyjących. Zadanie wykonaliśmy. Obliczyliśmy interesujące nas prawdopodobieństwo. Pozwólmy sobie teraz na kilka komentarzy i dygresji. Przypomnijmy najważniejszy wynik pomocniczy, który udowodniliśmy przed miesiącem.
Wyobraźmy sobie następującą grę. Mamy planszę o polach ponumerowanych od 0 do 100 i dwa pionki, stojące na początku na polu o numerze 0. Gracze wykonują ruchy na przemian. Gracz rzuca monetą i jeśli wypadnie reszka, to przesuwa swój pionek o 1 pole, a jeśli orzeł – o 5 pól. Wygrywa ten, kto pierwszy dojdzie do pola o numerze 100.
3, 7, 31, 211, 2311, ... – jaki jest następny wyraz tego ciągu? Jakiś czas temu taka zagadka pojawiła się na jednej z polskich rozrywkowych stron internetowych. Niemal od razu w komentarzach pod nią rozpoczął się spór o poprawne, prawdziwe rozwiązanie. Czytelnik zapewne zechce podjąć wyzwanie samodzielnego odnalezienia następnego elementu ciągu i jego ogólnej reguły. Zatem zatrzymajmy się tu i pozwólmy sobie na chwilę namysłu; w dalszej części tekstu pojawi się rozwiązanie (autorowi niniejszego tekstu zajęło kilka dłuższych chwil znalezienie formuły).
Kto by się spodziewał, że prawdziwe jest stwierdzenie: jeśli w sześcianie mieszczą się trzy jednakowe kulki, to zmieści się też czwarta tej samej wielkości!
W deltoidzie 7/2013 wykazaliśmy, że odcinek nie jest przeliczalny, posługując się tzw.
metodą przekątniową Cantora. Tym razem udowodnimy ten sam fakt, wykorzystując
pewną dwuosobową grę, której „planszą” jest zbiór
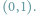
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Czasem jeden rysunek pozwala dowieść tak wiele...