Delta mi!

W geometrii dyskretnej przyjęło się mówić, że wielokąt jest wpisany w inny wielokąt, gdy ma wierzchołki na prostych zawierających boki tego drugiego wielokąta. Od czasu Hilberta tego zwrotu używa się i w przypadku "zwyczajnej" geometrii.

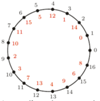
Na obrazku widać przenumerowanie szesnastu z 17 równo rozmieszczonych punktów na okręgu. Obok "normalnych" czarnych numerków podano dziwnie rozmieszczone czerwone. Zrobiono to w ten sposób, że nawinięto na ten okrąg półprostą, na której zaznaczono punkty odpowiadające kolejnym potęgom 3.

Czy Czytelnik zna grę w przeciąganie liny? Dwie drużyny ciągną dwa końce liny w przeciwne strony, a wygrywa ta, której uda się przeciągnąć linę na swoją stronę. Ściślej, gra kończy się w momencie wyjścia środka liny (zazwyczaj oznaczonego wstążką) z umówionego pola gry. Matematycy przypisują tę samą nazwę podobnej grze rozgrywającej się w dwóch (i więcej) wymiarach, w której to środek liny może poruszać się w wielu kierunkach, a nie tylko lewo-prawo. Trudno sobie jednak takie przeciąganie wyobrazić, dlatego przyjąłem termin gra w sumo.

2016 roku Nagroda Nobla z Fizyki została przyznana za teoretyczne odkrycia topologicznych przejść fazowych i topologicznych faz materii. Z kilku przyczyn nagroda ta była dość nietypowa. Komitet Noblowski zdecydował o wyróżnieniu nie pojedynczego, przełomowego odkrycia, ale raczej nagrodził wprowadzenie do fizyki nowych idei, które ukierunkowały i ukształtowały nasz sposób myślenia o fazach materii. Ponadto, co też nietypowe, nagrodzeni badacze to wyłącznie teoretycy, mimo że ich pomysły znalazły późniejsze potwierdzenie eksperymentalne. Komisja zdecydowała też o nierównym podziale nagrody: jej połowę otrzymał David J. Thouless, a drugą połową podzielili się F. Duncan M. Haldane oraz J. Michael Kosterlitz.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Czasem warto przetłumaczyć problem na inny język, aby łatwiej go rozwiązać.

Jednym z ważniejszych osiągnięć informatyki opartej o komputer kwantowy, które zresztą eksponujemy w tym numerze Delty, jest opracowanie efektywnego (wielomianowego od rozmiaru danych) algorytmu na rozkład dużych liczb na czynniki pierwsze. Wspaniały, budzący zachwyt wynik. Nie dość, że przepiękny, korzystający z bardzo ładnego fragmentu matematyki, to jeszcze pozwalający wierzyć, że komputer kwantowy złożony z 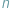kubitów jest istotnie lepszy od komputera klasycznego, zawierającego pamięć o 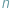bitach. Albo inaczej: że (też prezentowany w tym numerze) model obliczeń komputera kwantowego ma istotnie większą siłę wyrazu (przy założeniu wielomianowego czasu działania) niż klasyczny model Turinga czy inne równoważne.

Jak można dowiedzieć się z rozlicznych filmów akcji, nieodłączną częścią życia każdego szanującego się tajnego agenta jest wymiana tajnych informacji, najlepiej takich z wielką, czerwoną pieczęcią "Top Secret". Jeśli agent ma taką możliwość, najlepiej przekazać teczkę pełną tajemnic osobiście, jednak jest to luksus, na który może on pozwolić sobie w niewielu sytuacjach, gdyż nierzadko odbiorca tych tajemnic znajduje się na drugim końcu globu. W tej sytuacji konieczne staje się odpowiednie zaszyfrowanie naszych sekretów, aby nawet w przypadku przechwycenia ich przez oślizgłe macki szwarccharakterów, pozostały one sekretami.

W poniższym artykule postaramy się przybliżyć Czytelnikowi niektóre podstawowe pojęcia algebry wieloliniowej nad liczbami zespolonymi, która jest podstawą rozważań w kwantowej teorii obliczeń. Bez zbędnej zwłoki przystąpimy od razu do konkretów.

Jeżeli określimy dodawanie i mnożenie punktów płaszczyzny, z wyróżnionymi punktami 0 i 1, w sposób przedstawiony na rysunku, to otrzymamy liczby zespolone...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

...z których żadne dwie nie są równoległe, a żadne trzy nie mają punktu wspólnego... tworzą cztery trójkąty - to każdy widzi i nikt się nie dziwi.

Oto kilka zadań związanych z istnieniem i własnościami pewnych krzywych lub łamanych na płaszczyźnie i w przestrzeni trójwymiarowej.

- Lolek, chodź, pokażę Ci jedną stronę w Internecie...

W miejscowości 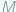jest fryzjer, nazwijmy go superfryzjerem, który strzyże tych i tylko tych mieszkańców miejscowości, którzy nie strzygą siebie samych. Czy superfryzjer strzyże siebie samego? Chwila namysłu pokazuje, że obie możliwości są wykluczone: nie może on strzyc siebie samego, bo strzyże tylko tych, którzy siebie sami nie strzygą; gdyby zaś sam się nie strzygł, to musiałby się strzyc, bo strzyże wszystkich tych, którzy sami się nie strzygą. A zatem, superfryzjer nie może istnieć! Pokażemy jak z powyższego faktu otrzymać różne twierdzenia matematyczne, odpowiednio definiując mieszkańców miejscowości 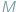oraz to, kto kogo strzyże.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Prezentujemy kilka zadań wraz z "rozwiązaniami" i... lepszymi rozwiązaniami...

Ustalenie wspólnego stanowiska przez grupę ludzi wymaga często w pierwszym kroku wyboru metody podjęcia zbiorowej decyzji. Kluczowe stają się wówczas pytania: Jaka metoda jest sprawiedliwa? Jaka metoda najlepiej odzwierciedli preferencje członków grupy?

Poniższa opowieść była na tyle ważna dla młodego, zaledwie dwudziestoletniego, matematyka Évariste'a Galois, że poświęcił ostatni dzień przed pojedynkiem, aby spisać ją w liście do przyjaciela. Niestety, nie dostał od losu szansy na kontynuowanie swoich prac, ale jakiś czas po jego śmierci matematycy zrozumieli znaczenie jego pomysłów. Ślady teorii, z której zarysem Czytelnik zapoznać się może w dalszej części artykułu, odnaleźć można w wielu gałęziach współczesnej matematyki. Jej bezpośrednim następstwem jest wiele efektownych rozwiązań problemów, których ludzkość szukała przez setki lat: nierozwiązalność (przez pierwiastniki) równań wielomianowych stopnia 5 lub wyższego, niekonstruowalność pewnych wielokątów foremnych (cyrklem i linijką), a także niewykonalność klasycznych konstrukcji geometrycznych, czyli podwojenia sześcianu, trysekcji kąta i kwadratury koła.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W LXVIII Olimpiadzie Matematycznej uczestniczyło 1495 uczniów, zatem o 324 osoby więcej niż rok wcześniej, do zawodów stopnia drugiego zakwalifikowano 632 uczniów, a do zawodów stopnia trzeciego - 154 uczniów. Zapewne wynika to z pojawienia się w pierwszym stopniu sporej liczby zadań stosunkowo łatwych, a już na pewno niewymagających szczególnego przygotowania...

Odcinek 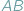widać z punktu 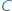pod kątem 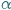, gdy 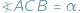Z twierdzenia o kątach wpisanych wynika, że jeśli punkty 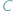i 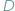leżą na okręgu po tej samej stronie jego cięciwy 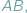to widać ją z 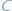i 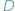pod tym samym kątem (Rys. 1).

W Delcie 7/2017 przedstawiliśmy kilka "olimpijskich" zastosowań twierdzenia Combinatorial Nullstellensatz. Okazuje się, że zamiast "zwykłych" wielomianów wielu zmiennych możemy rozważać wielomiany o współczynnikach będących resztami z dzielenia przez pewną liczbę pierwszą 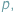z dodawaniem i mnożeniem modulo 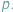Poniżej przedstawimy trzy klasyczne twierdzenia, których proste dowody są oparte na Combinatorial Nullstellensatz w wersji "resztowej". Twierdzenia te są szczególnie bliskie zastosowaniom olimpijskim.

Martin Gardner został w 1967 roku poproszony przez wydawnictwo Greenwood Press o pomysły na nowe czasopisma. Jako efekt jego rekomendacji powstały wówczas Journal of Recreational Mathematics (JRM) oraz Word Ways - Journal of Recreational Linguistics (JRL).

Wyniki XXXIV Ogólnopolskiego Sejmiku Matematyków, Szczyrk, 8-11 VI 2017