Paradoksy rachunku prawdopodobieństwa
Rachunek prawdopodobieństwa jest tą dziedziną matematyki, w której istnieje szczególnie dużo paradoksów. Związane jest to z naszymi błędnymi wyobrażeniami o losowości.
Rachunek prawdopodobieństwa jest tą dziedziną matematyki, w której istnieje szczególnie dużo paradoksów. Związane jest to z naszymi błędnymi wyobrażeniami o losowości.
W artykule „Gra w 20 pytań” omówiliśmy sposób gry z graczem, który nie kłamie. A jak postępować z graczem, który kłamie? Czy jesteśmy zupełnie bezradni?
Gry, zagadki, paradoksy Mała Delta
... to dobrze znana gra.
Geometrie nieeuklidesowe Co to jest?
Formułując szczególną teorię względności (STW) Einstein nie używał pojęcia czasoprzestrzeni – zbioru zdarzeń, operował oddzielnie pojęciami czasu i przestrzeni. Pojęcie czasoprzestrzeni pojawiło się podczas odczytu wygłoszonego w 1908 roku przez Hermanna Minkowskiego w Kolonii. Minkowski pokazał, że do opisu STW wygodnie jest posługiwać się szczególną czterowymiarową geometrią, nazwaną później jego nazwiskiem.
Każdy uczeń szkoły średniej wie, że gdy zna się współczynniki trójmianu kwadratowego, to można jawnymi wzorami wyrazić pierwiastki tego trójmianu. We wzorach tych wykonuje się (skończoną liczbę razy) tylko cztery działania arytmetyczne i pierwiastkowanie.
Teoria Mnogości O tym, czego nie ma
Cóż prostszego, jak stworzyć zbiór z dowolnych prawdziwych lub wymyślonych obiektów! Czyż zbiór nie jest po prostu pewną konstrukcją myślową? Wystarczy zatem pomyśleć o owych obiektach jako o elementach jednego zbioru – i już.
Jak wiele innych ważnych twierdzeń matematyki, zasadnicze twierdzenie algebry,
udowodnione przez Carla Friedricha Gaussa w ostatnim roku osiemnastego stulecia,
informuje nas, że pewne obiekty nie istnieją. Mianowicie, nie ma takiego, różnego od
stałej, wielomianu zmiennej zespolonej, który nie znikałby w żadnym punkcie
płaszczyzny zespolonej
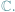
Płaszczyznę
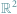 można wyposażyć w działania dodawania i mnożenia jej
punktów. Dlaczego nie można tego zrobić z przestrzenią
można wyposażyć w działania dodawania i mnożenia jej
punktów. Dlaczego nie można tego zrobić z przestrzenią
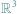 ?
?
Jeśli liczba naturalna
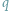 jest największą liczbą pierwszą, to...
jest największą liczbą pierwszą, to...
Zwykłe siodło do konnej jazdy ma dwa łęki i dwie klapy – z przodu i z tyłu jest podniesione do góry, z obu boków opada w dół. Jest przy tym wszędzie krzywe, czyli niepłaskie...
Dla każdej liczby naturalnej
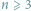 można, oczywiście, narysować wielokąt,
który ma
można, oczywiście, narysować wielokąt,
który ma
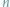 boków. A jak to będzie z wielościanami o zadanej z góry liczbie
krawędzi?
boków. A jak to będzie z wielościanami o zadanej z góry liczbie
krawędzi?
Stereometria Kącik przestrzenny
Czasami, gdy zbytnio bujamy w obłokach, słyszymy od innych zejdź na ziemię! Kto by pomyślał, że ta zazwyczaj dość nieprzyjemna uwaga może być niekiedy cenną wskazówką do zadań ze stereometrii.
Jak wiadomo, pochodna opisuje zmiany danej wielkości (np. tak działa prędkościomierz w samochodzie). Z kolei całka opisuje sytuację odwrotną – odtwarza daną wielkość z jej zmienności (tak np. działa licznik energii elektrycznej).
W wielu zadaniach dane są trzy punkty, które albo są współliniowe, albo należy to o nich udowodnić. Wygodnym narzędziem bywa wtedy Twierdzenie Menelaosa.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Planimetria Stowarzyszenie na rzecz Edukacji Matematycznej
W roku szkolnym 2010/2011 Stowarzyszenie na rzecz Edukacji Matematycznej jest
organizatorem LXII edycji Olimpiady Matematycznej. Od września do grudnia
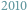 roku uczestnicy Olimpiady Matematycznej zmagali się z dwunastoma
zadaniami domowymi pierwszego etapu zawodów
roku uczestnicy Olimpiady Matematycznej zmagali się z dwunastoma
zadaniami domowymi pierwszego etapu zawodów
Skojarzenia to bardzo popularny temat. Pojawiają się w różnych miejscach zarówno w informatyce, jak i w matematyce dyskretnej.
Jednym z głównych narzędzi służących do matematycznego opisu otaczającego nas świata są równania różniczkowe zwyczajne i cząstkowe.
Pomysł tego artykułu powstał na lekcji matematyki w I klasie gimnazjum. Rozwiązywałem
z uczniami zadanie z podręcznika wydanego przez Gdańskie Wydawnictwo
Oświatowe: który z narysowanych trójkątów jest przystający do trójkąta
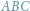 ?
?
Gry, zagadki, paradoksy Mała Delta
Nierzadko zbywamy kandydatów na twierdzenia matematyczne niemal pogardliwym
określeniem: oczywiste! Liczba
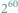 jest większa od
jest większa od
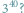 Oczywiste!
Środek okręgu opisanego na trójkącie leży wewnątrz trójkąta? Oczywiste!
Oczywiste!
Środek okręgu opisanego na trójkącie leży wewnątrz trójkąta? Oczywiste!
Pytanie postawione w tytule wydaje się dziwne. Przecież wiadomo co najmniej od czasów Platona, że wielościanów foremnych jest pięć typów: czworościan foremny, sześcian oraz ośmiościan, dwunastościan i dwudziestościan – wszystkie foremne. Łatwo też pokazuje się, że nie może być ich więcej. W czym zatem problem?
Rachunek prawdopodobieństwa Omega
Dwóch graczy gra w piłkę do 60 punktów. Przy stanie 50:30 trzeba przerwać grę. Jak sprawiedliwie podzielić pulę?