Delta mi!

Istnieje zaskakujący związek między okręgiem wpisanym w trójkąt i okręgiem na nim opisanym.

Rozpowszechnione jest przeświadczenie, że znaczna część dowodów geometrycznych prowadzonych przez mędrców Złotego Wieku Grecji, a więc czasów po zwycięskich wojnach perskich i kojarzących się nam np. z Peryklesem, wyglądała tak, iż był to rysunek ze słownym komentarzem: Patrz. Niezależnie od podziwu dla intelektualnej estetyki takich dowodów podejrzewamy, że dotyczyły one problemów mało skomplikowanych, rozumowań wymagających jednego kroku myślowego.

Najbardziej zachęcającym aspektem uprawiania matematyki (oczywiście, poza niezaprzeczalnym pięknem matematycznych teorii) jest jej szeroka gama zastosowań i olbrzymia efektywność w modelowaniu świata rzeczywistego. Popularne jest nawet określenie "niepojęta skuteczność matematyki" (np. w pracy E. Wignera pod tożsamym tytułem The Unreasonable Effectiveness of Mathematics in the Natural Sciences). Warto jednak pamiętać, że modelowanie matematyczne jest czymś więcej niż tylko wyjątkowo użytecznym młotkiem wbijającym kolejne gwoździe, na których opiera się nasze zrozumienie wszechświata. Dzięki matematyce możemy modelować nie tylko to, co jest rzeczywiste (w jakimkolwiek tego słowa znaczeniu), ale też wszystko, co tylko potrafimy sobie wyobrazić.

W pewnym mieście podjęto decyzję o budowie nowego osiedla. Postanowiono, że będzie to szereg ośmiu budynków. Przyjęto, że żadne trzy stojące obok siebie budynki nie mogą być tej samej wysokości. Ustalono, że budynki będą mieć wysokości równe odpowiednio: 5, 10, 10, 15, 25, 25, 30 i 45 metrów...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Zechciejcie państwo wysłuchać dziś krótkiej opowieści z królestwa geometrii. Za siedmioma górami matematycznych podręczników, za siedmioma rzekami matematycznych równań, za siedmioma lasami matematycznych sprzeczności znajdowała się symediana. Dziś symediana ujrzy światło dzienne...

Korzystając z tytułowego pomysłu oraz z rysunku lub drobnych jego modyfikacji, można udowodnić szereg twierdzeń z różnych działów matematyki.

W Delcie 1/2015 Łukasz Rajkowski oszacował, kiedy należy spodziewać się końca świata. Narzędziem użytym w tej analizie było wnioskowanie bayesowskie. Nie od dziś wiadomo, że należy je stosować z odpowiednią ostrożnością oraz dbałością o założenia i interpretacje. Dlaczego? Zastanówmy się nad poniższym prostym przykładem, gdzie na użytek tych, którzy nie wyobrażają sobie prawdopodobieństwa bez kul w urnach lub rzutów monetą, został wykorzystany ten ostatni model.

Zająłem się ciekawym problemem dotyczącym centrów trójkąta. Ciekawym, bo łatwym do wyobrażenia, a w pewnych aspektach nawet bardzo trudnym.

Niektórzy znajdują co rano na progu swojego domu butelkę ze świeżym mlekiem. Kubuś Puchatek każdego ranka znajduje tam 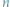garnczków miodu. Garnczki są różnej wielkości i Kubuś każdego dnia stara się opróżniać je w innej kolejności...

Drogi Czytelniku, czy zdarza Ci się czasem doświadczać bólu pleców w odcinku lędźwiowym? Jest to całkiem prawdopodobne, gdyż wedle sondażu ponad połowa ankietowanych Polaków oświadczyła, że cierpi z tego powodu, a co szósty badany stwierdził, że bóle kręgosłupa odczuwa bardzo często. A jeżeli tak właśnie jest, to czy zdajesz sobie sprawę z tego, że przyczyna tego bólu może być bardzo mocno związana ze sposobem, w jaki używasz swoich szczęk?

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Jak wszystkim wiadomo, około -300 roku dyrektor Biblioteki Aleksandryjskiej imieniem Euklides napisał dzieło, które jest znane pod późniejszym łacińskim tytułem Elementy. W dziele tym z następujących pięciu postulatów wyprowadził całą geometrię (tę nauczaną w szkole i zwaną euklidesową) i całą arytmetykę.

Każda ptaszyna swym własnym głosem Pana Boga chwali. Tym przysłowiem odpowiedziałem podczas obrony pracy doktorskiej na pytanie Profesora Andrzeja Mostowskiego, czemu zbudowałem aksjomatykę geometrii eliptycznej, podczas gdy można tę geometrię uprawiać analitycznie (czyli rachunkowo)...

Bryła to stworzenie, z którym większość z nas poznała się w szkole podstawowej i które było przez nas oswajane przez kolejne lata edukacji. Znamy bliżej różne rodziny brył, takie jak wielościany, graniastosłupy, bryły obrotowe, foremne, platońskie. Oczywiście, można produkować nowe stworzenia, łącząc czy tnąc "podstawowe" gatunki, a jedynym ograniczeniem jest nasza wyobraźnia.

Oto dwa zupełnie niepodobne zadania, które można rozwiązać w zaskakująco podobny sposób. W obydwu przypadkach rozwiązanie okazuje się znacznie prostsze, niż można by się w pierwszej chwili spodziewać.

Zawód matematyka, jak powiada jeden z uprawiających go kolegów, polega na rozwiązywaniu zadań z treścią. Takich zadań pełne są podręczniki do nauczania matematyki na różnych poziomach edukacji. Zazwyczaj jednak matematyk zajmuje się zadaniami, których do tej pory nikt nie rozwiązał; najczęściej zaczynają się one od "wykaż, że". Skąd się biorą? Z zadziwienia, z zachwytu, wreszcie z ciekawości, która rodzi pytania: "jak?", "dlaczego?". Takie zadziwienie, taki zachwyt czy taka ciekawość pojawiają się w każdym wieku, wystarczy mieć otwarte oczy i otwarty umysł, wsparte zainteresowaniem popychającym do dążenia tropem zauważonych śladów.

Kryształy to jedne z najbardziej osobliwych elementów świata przyrody. Materiały krystaliczne wykazują niemal niespotykaną naturalną tendencję do tworzenia wielościanów. Piętnastometrowe kryształy w Meksyku czy dwumilimetrowe kryształki soli w naszej kuchni - wszystkie swą szczególną postać zawdzięczają uporządkowanemu rozmieszczeniu atomów, jonów lub cząsteczek.

Zderzenie z asteroidą, wojna nuklearna, globalny potop, przebiegunowanie Ziemi... liczba katastrof oznaczających koniec ziemskiej cywilizacji powinna skłonić nas do traktowania każdego spokojnego poranka, kiedy przewracamy się leniwie z boku na bok zamiast skwierczeć w ogniu Apokalipsy, jako prawdziwego cudu. Mnogość śmiercionośnych zagrożeń sprawia, że ludzkość od zamierzchłych czasów stara się przewidzieć datę (choćby przybliżoną) własnego końca, nie przejmując się zbytnio kolejnymi niepowodzeniami w tej materii. Większość z proponowanych terminów pochodziła od astrologów, numerologów lub przywódców religijnych. Zgodnie z powiedzeniem Hugo Steinhausa "Matematyk zrobi to lepiej" spróbujmy zastanowić się, co ma do powiedzenia w kwestii terminu Końca Świata Królowa Nauk.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W LXV Olimpiadzie Matematycznej wzięło udział 1167 uczniów. Do zawodów drugiego stopnia zakwalifikowano 507 osób, a do finału, zorganizowanego przez Zespół Szkół Ogólnokształcących im. Stefana Żeromskiego przy ul. Sienkiewicza 1 w Iławie, zaproszono 138 młodych ludzi.

Przekształcenie afiniczne płaszczyzny to takie różnowartościowe przekształcenie płaszczyzny w siebie, przy którym obrazem każdej prostej jest prosta. Wszystkie podobieństwa spełniają te warunki, ale nie tylko one...

W tym artykule ilustrujemy potęgę logarytmów w projektowaniu efektywnych algorytmów i obliczeń. Myślenie, w tle którego stoi logarytm, ukryty lub widoczny, nazwaliśmy myśleniem logarytmicznym. Stanowi ono jedną z podstawowych kompetencji niezbędnych przy efektywnym rozwiązywaniu rzeczywistych problemów informatycznych. Pokazujemy również - co może być ciekawe dla nauczycieli matematyki - jak wprowadzić pojęcie logarytmu, nie odwołując się do matematycznego formalizmu, a posługując się koncepcyjnym modelem redukcji rozmiaru problemu w każdym (lub w co drugim) kroku co najmniej o połowę. Może Cię zdziwić, że ta idea prowadząca do logarytmu występuje w algorytmie Euklidesa, który został opisany niemal 2000 lat przed wynalezieniem logarytmu przez Napiera.