Matematyka Klub 44 - Matematyka
Klub 44M - zadania III 2020
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Zadania z myszką – matematyka
Jak co miesiąc, trzy ciekawe zadania z matematyki...
Matematyka Kącik początkującego olimpijczyka
Według legendy pod koniec XVIII wieku działa się następująca rzecz. Pewien nauczyciel kazał swoim uczniom dodać wszystkie liczby od 1 do 40, aby mieć przez dłuższą chwilę spokój. Wszyscy, z wyjątkiem jednego, wykonywali pracowicie kolejne dodawania i zazwyczaj popełniali błędy...
Celem tego artykułu jest wykazanie prawdziwości nierówności 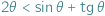 dla dowolnego kąta ostrego
dla dowolnego kąta ostrego 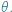 Podaną nierówność można łatwo udowodnić, używając rachunku różniczkowego. Można jednak zadać pytanie: czy da się tego uniknąć, czy można ją wykazać krócej, używając przy tym jedynie elementarnej geometrii. Okazuje się, że tak.
Podaną nierówność można łatwo udowodnić, używając rachunku różniczkowego. Można jednak zadać pytanie: czy da się tego uniknąć, czy można ją wykazać krócej, używając przy tym jedynie elementarnej geometrii. Okazuje się, że tak.
Być może nie wypada zadawać tytułowego pytania w numerze marcowym, gdyż w tym miesiącu obchodzone jest wspaniałe święto tej największej bodaj celebrytki pośród liczb rzeczywistych, jednak Delta nie pozwoli zakneblować sobie ust poprawnością polityczną. Tym bardziej, że w Internecie roi się od plotek i pogłosek na ten temat. Zamieszanie rozpoczęło się od utworzonego w dobrej wierze memu (zamieszczony poniżej), którego autor w poetycki sposób opisywał rzekomą, mistyczną własność 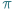 - jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.
- jej rozwinięcie dziesiętne miałoby skrywać wszelkie tajemnice tego świata i odpowiedzi na wszystkie fundamentalne dla ludzkości pytania.
W pewnym zakładzie karnym przebywa stu skazanych, ponumerowanych liczbami od 1 do 100: 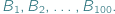 Strażnik zaproponował im następującą grę: sto kartek z ich numerami umieszcza w stu skrytkach, po jednej kartce w każdej skrytce. Sposób rozmieszczenia kartek nie jest znany więźniom. Następnie strażnik pozwala każdemu z więźniów sprawdzić dokładnie połowę skrytek. Sprawdzający wchodzi do pokoju ze skrytkami sam, a po swojej turze musi zostawić pokój w stanie nienaruszonym i jedynie poinformować nadzorcę, czy odnalazł swój numer, czy też nie. Nie komunikuje się później z pozostałymi więźniami. Osadzeni wygrywają wyjście na wolność wtedy i tylko wtedy, gdy każdy z nich zdoła odnaleźć swój numer. Jaka jest szansa na to, że im się to uda?
Strażnik zaproponował im następującą grę: sto kartek z ich numerami umieszcza w stu skrytkach, po jednej kartce w każdej skrytce. Sposób rozmieszczenia kartek nie jest znany więźniom. Następnie strażnik pozwala każdemu z więźniów sprawdzić dokładnie połowę skrytek. Sprawdzający wchodzi do pokoju ze skrytkami sam, a po swojej turze musi zostawić pokój w stanie nienaruszonym i jedynie poinformować nadzorcę, czy odnalazł swój numer, czy też nie. Nie komunikuje się później z pozostałymi więźniami. Osadzeni wygrywają wyjście na wolność wtedy i tylko wtedy, gdy każdy z nich zdoła odnaleźć swój numer. Jaka jest szansa na to, że im się to uda?
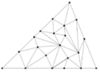
Rys. 1. Triangulacja trójkąta
Poprzez triangulację będziemy rozumieć podział figury na trójkąty (Rys. 1). W dalszej części artykułu będziemy zajmować się kolorowaniem wierzchołków triangulacji pewnego trójkąta...
Rozpocznijmy od przypomnienia, czym jest trójkąt geodezyjny. Mając dane dwa punkty na powierzchni (powiedzmy, że leżące odpowiednio blisko siebie), najkrótszą łączącą je krzywą leżącą na tej powierzchni nazwiemy geodezyjną. Dla przykładu - na płaszczyźnie tę rolę pełnią odcinki, a na sferze łuki tzw. okręgów wielkich. Przez trójkąt geodezyjny rozumiemy obszar wyznaczony przez trzy punkty, zamknięty między łączącymi je geodezyjnymi. Kąt w wierzchołku takiego trójkąta liczymy jako kąt między stycznymi do odpowiednich krzywych geodezyjnych.
Matematyka Zadania z myszką – matematyka
Jak co miesiąc, trzy ciekawe zadania z matematyki...
Geometria Kącik początkującego olimpijczyka
O stosowaniu trygonometrii w zadaniach olimpijskich.
Zacznijmy od przypomnienia zadania 766 z Klubu 44M (Delta 9/2018)...
Trójkąt Pascala zna praktycznie każdy. Widoczny poniżej z lewej strony trójkąt ma tę własność, że każda liczba jest sumą dwóch liczb stojących bezpośrednio nad nią (z wyłączeniem wierzchołka trójkąta oraz jego prawego i lewego boku, gdzie znajdują się jedynki). Z kolei w trójkącie po prawej stronie każda liczba jest sumą dwóch liczb stojących bezpośrednio pod nią. Na jego prawym oraz lewym boku znajdują się odwrotności kolejnych liczb naturalnych - liczby harmoniczne. Taki obiekt nazywa się trójkątem harmonicznym. Konstrukcję obu trójkątów można oczywiście kontynuować w nieskończoność...
Znany jest wzór na sumę kątów w trójkącie:
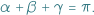 |
Dotyczy on oczywiście trójkątów na płaszczyźnie. Jaki związek ma płaskość (lub zakrzywienie) z powyższym wzorem? O tym za chwilę.
Jeśli czytasz ten tekst, to świetnie się składa, możesz poznać drobny fragment topologii i zmierzyć się z następującym pytaniem: Ile topologicznie różnych figur można ułożyć na płaszczyźnie z sześciu zapałek, które stykają się tylko końcami?
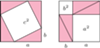
Są twierdzenia łatwe i trudne do udowodnienia. Zazwyczaj im mocniejsze sformułowanie, obejmujące więcej przypadków, tym trudniej się je dowodzi. Tak jest na przykład z twierdzeniem cosinusów i twierdzeniem Pitagorasa, które jest jego szczególnym przypadkiem. Łatwiej jest udowodnić twierdzenie Pitagorasa; można to zrobić nawet w sposób zrozumiały dla przedszkolaka (zobacz rysunek obok). Do dowodu twierdzenia cosinusów trzeba przynajmniej wiedzieć, co to cosinus, w szczególności kąta rozwartego.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Matematyka Zadania z myszką – matematyka
Jak co miesiąc, trzy ciekawe zadania z matematyki...
Przypuśćmy, że dane mamy dwa czworokąty wypukłe 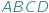 i
i 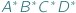 takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...
takie, że każdemu bokowi jednego odpowiada pewien równoległy doń bok drugiego, a każdej przekątnej - równoległa przekątna. Na pierwszy rzut oka wydawać by się mogło, że takie czworokąty muszą być podobne, jest jednak druga możliwość - wówczas czworokąty te są bliźniacze...
Algebra Kącik początkującego olimpijczyka
Tożsamości algebraiczne, w których pojawia się suma sześcianów trzech liczb.
Na początek krótka zagadka: co jest większe, 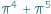 czy
czy 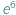 ? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
? Drogi Czytelniku! Nie wysilaj się. Nie masz szans raczej tego poprawnie ocenić...
Teoria Mnogości Nieskończoność
W poprzednim odcinku zastanawialiśmy się, czy istnieje "nieskończoność" pomiędzy licznością zbioru liczb naturalnych i licznością zbioru liczb rzeczywistych. Pora na ostatni etap naszej podróży. Będzie to etap jeszcze dalej prowadzący w nieskończoność - będziemy rozważać i konstruować coraz większe "nieskończoności". Okaże się, że jest ich bardzo nieskończenie wiele. Może aż za bardzo.
Dawno temu... w czasach bez Internetu, bez gier komputerowych i smartfonów dzieci bawiły się w chowanego. Na początku zabawy trzeba było oczywiście wyznaczyć osobę, która będzie szukać. Uczestnicy ustawiali się w koło i ktoś odliczał: Raz, dwa, trzy, wychodź ty, i wówczas szósta osoba (odliczanka ma 6 sylab) wychodziła z kółka. Procedurę tę powtarzano aż do momentu, gdy w kółku pozostała jedna osoba - to był pierwszy szukający. Istnieje wiele wierszyków-odliczanek. Moją ulubioną jest odliczanka 15-sylabowa: Mama daje jeść, tata daje pić, a ty sobie idź.
Już rok po śmierci Gaussa (w 1856 r.) ukazała się książka wspomnieniowa jego wieloletniego przyjaciela Wolfganga Sartoriusa von Waltershausena Zum Gauss Gedächtniss. Trzeba o niej wiedzieć co najmniej z dwóch powodów. Stąd pochodzi najsłynniejszy aforyzm z matematyką w roli głównej. Jako teoretyk liczb przytoczę go z przyjemnością w pełnej postaci: Matematyka jest królową nauk, a arytmetyka królową matematyki.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty