Matematyka Kącik początkującego olimpijczyka
Gdy zadaniu nie podołasz, to załatwi je niezmiennik
O pożytkach płynących z faktu, że niektóre własności obiektów zostają zachowane po poddaniu ich wybranym przekształceniom.
Matematyka Kącik początkującego olimpijczyka
O pożytkach płynących z faktu, że niektóre własności obiektów zostają zachowane po poddaniu ich wybranym przekształceniom.
W poprzedniej części tej opowieści o nieskończonościach rozważaliśmy twierdzenie Cantora, które stanowi, że żaden zbiór 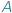 nie jest równoliczny ze zbiorem jego podzbiorów
nie jest równoliczny ze zbiorem jego podzbiorów 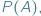 co symbolicznie notujemy
co symbolicznie notujemy 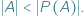 Szczególnie zajmowaliśmy się przypadkiem, gdy
Szczególnie zajmowaliśmy się przypadkiem, gdy 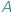 jest zbiorem liczb naturalnych
jest zbiorem liczb naturalnych 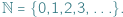
Niniejszy odcinek jest ostatni z serii. Przez niemal rok, wraz z Łukaszem Rajkowskim, próbowaliśmy pokazać Czytelnikowi, co ciekawego, a przede wszystkim - co zaskakującego, wiąże się z kryptologią. Naszą wielką nagrodą będzie, gdy - po przeczytaniu tych 9 odcinków - choć niewielka część Czytelników chociaż przez chwilę zawaha się, gdy w życiu codziennym będzie stwierdzać, że czegoś się nie da...
Liczby przedstawiać można na wiele sposobów. Jako dzieci liczyliśmy na palcach czy używając patyczków lub liczydła. Ten sposób przedstawiania liczb - przez fizyczną liczbę pewnych obiektów - nazywany jest kardynalnym. Jest bardzo prosty: tworzy się słowo lub symbol oznaczające jeden, a następnie powtarza się odpowiednią ilość razy...
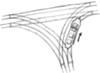
Rys. 1
Podejrzewam, że znakomita większość Czytelników Delty, nawet jeśli nie mieszka, to miała okazję przebywać w dużych miejskich aglomeracjach z rozbudowaną siecią tramwajową i zetknąć się z miejscem, w którym spotykają się trzy dwutorowe odcinki trasy...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W zawodach I stopnia LXX Olimpiady Matematycznej wzięło udział 1324 uczniów. Do zawodów stopnia II zakwalifikowano 598 uczniów, a do zawodów stopnia III - 141.

W XIV Olimpiadzie Matematycznej Juniorów (dawniej Gimnazjalistów), adresowanej do uczniów gimnazjum oraz szkół podstawowych, wzięło udział 11 592 uczniów z 1486 szkół (w tym 7189 uczniów z 924 szkół podstawowych). W zawodach II stopnia wzięło udział 1753 uczniów z 877 szkół (w tym 923 uczniów z 498 szkół podstawowych). W zawodach III stopnia wzięło udział 257 uczniów ze 166 szkół (w tym 132 uczniów z 93 szkół podstawowych).
Matematyka Kącik początkującego olimpijczyka
Zadania z wykorzystaniem indukcji prostej, głębokiej i silnej.
Zastosowania matematyki Nowe pomysły
Walka z przestępczością jest jednym z podstawowych zadań każdej władzy, od jej skuteczności zależy jakość życia obywateli. Nic więc dziwnego, że rozmaite instytucje publiczne starają się zaprzęgać do tego celu metody statystyczne i uczenie maszynowe. Opowiem tu pokrótce, jak wygląda w praktyce "maszynowe" przewidywanie przestępstw i czy daje zadowalające rezultaty. Skupię się na miastach Ameryki Północnej, ponieważ tam tego typu systemy są najbardziej rozwinięte. Aby uniknąć rozważań natury prawnej, przestępstwem będę dla uproszczenia nazywał każde złamanie prawa, niezależnie od tego, czy formalnie kwalifikuje się jako czyn zabroniony, wykroczenie czy przestępstwo.

Każdy widział kiedyś bańki mydlane. Nie ma co ukrywać, są one okrągłe. Tylko dlaczego?
Problem 2. Do dyspozycji mamy nieograniczoną liczbę prostopadłościennych cegieł o jednakowym rozmiarze i masie. Cegły ustawiamy jedna na drugiej - bez użycia żadnych materiałów klejących. Jak bardzo najwyżej położona cegła może być wysunięta w stosunku do cegły położonej najniżej? Rozkład masy w każdej cegle jest jednorodny.
W poprzednim odcinku naszej sagi przedstawiliśmy miłosną historię Aldony i Bogumiła. Poniżej prezentujemy jej dość dramatyczną kontynuację, widzianą oczami Aldony...
Istnieje nieskończenie wiele brył geometrycznych, którymi matematycy nigdy dotąd się nie zajmowali, bo po prostu nie były one dla nich wystarczająco interesujące. Czasem jednak zdarza się, że i niematematyk natrafi na coś, co z pewnych powodów okaże się ważne, a wtedy robi się naprawdę ciekawie.
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Stereometria Kącik początkującego olimpijczyka
Rozpatrując siatkę, odpowiedni przekrój lub rzut, możemy niekiedy sprowadzić zadanie z geometrii przestrzennej do zadania z planimetrii.
W zeszłym roku (już po raz drugi!) miałem przyjemność pełnić funkcję tutora podczas obozu Maths Beyond Limits. Poprowadziłem dwie serie zajęć, z których jedna dotyczyła teorii mnogości. Starając się dać uczestnikom podstawy arytmetyki zbiorów nieskończonych w zajmujący i bezbolesny, mam nadzieję, sposób, pokazałem ciekawe zadania, wykorzystujące różne metody i pomysły. Jeden z nich jest szczególnie warty uwagi...
Skończył się mecz - najważniejsze wydarzenie tygodnia. Po burzliwej wymianie zdań na jego temat trzej przyjaciele: Długi, Gruby i Ludek wracali do domu. Nagle Ludek zapytał o zadanie z matematyki, które było na jutro. Długi i Gruby stanęli jak zaczarowani. Zapomnieli o zadaniu. W necie na chwilę się zagotowało! Nastała cisza przerywana wiadomościami przychodzącymi na komórki. Nikt z klasy jeszcze zadania nie zrobił. Zadanie było krótkie: Jak gruba powinna być moneta, aby szansa, że wyląduje ona na krawędzi, wynosiła 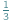 ?
?
Człowiek to istota nie tylko myśląca, ale i mierząca - można by rzec górnolotnie, że mierzenie (rozmiarów wrogiej armii, zaopatrzenia spichrzów, stanu skarbca itp.) leży u podstaw naszej cywilizacji. W języku matematyki miara jest definiowana przez następujące, zdroworozsądkowe warunki...
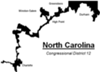
Zastosowania matematyki Co to jest?
W końcu 2016 roku sąd okręgowy stanu Wisconsin po raz pierwszy w historii wyborów do Kongresu USA zdecydował o zmianie dystryktów wyborczych. Uzasadnieniem było to, że jednomandatowe dystrykty wyborcze dawały niesprawiedliwą przewagę Republikanom. Zdaniem sądu partia ta, mając przewagę w kongresie stanowym, po spisie powszechnym 2010 roku wyznaczyła dogodny dla siebie układ dystryktów.
W poprzednim odcinku sprawdziliśmy, że zbiór liczb naturalnych jest równoliczny ze zbiorem liczb wymiernych (także zbiór liczb całkowitych jest równoliczny z każdym z nich). Inaczej mówiąc, można ustawić liczby wymierne w pary z liczbami naturalnymi w taki sposób, że każda liczba wymierna stoi w parze z dokładnie jedną liczbą naturalną i każda liczba naturalna stoi w parze z dokładnie jedną liczbą wymierną. Można też powiedzieć, że wszystkie liczby wymierne da się zakwaterować w hotelu Hilberta.
Wyobraźmy sobie następującą wakacyjną historię miłosną, która miała prawo się zdarzyć przed nastaniem ery wszechobecnych mediów społecznościowych...
Matematyka Klub 44 - Matematyka
Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty
Analiza Kącik początkującego olimpijczyka
Kwadrat liczby rzeczywistej jest nieujemny (fanfary!).
Kiedy jest najlepszy moment na powiedzenie sakramentalnego "tak"? Czy obecny obiekt westchnień jest osobą, z którą spędzisz resztę życia? Ile związków musi się rozpaść, żeby stworzyć stabilną relację? Pewnie wiele osób zadaje (lub wkrótce zada) sobie takie pytania. Ciężko uwierzyć, że matematyka i algorytmika mogą nam pomóc również w romantycznych rozważaniach i sercowych dylematach. Wszystko sprowadza się przecież do określenia momentu, kiedy należy przerwać szukanie i podjąć decyzję, a ten problem jesteśmy w stanie wymodelować matematycznie.