Delta mi!

Czysty zeszyt, cyrkiel, linijka, kątomierz, liniuszek - standardowy szkolny ekwipunek lekcji geometrii. Ale istnieją również inne geometrie, w których do konstrukcji figur nie jest potrzebne żadne oprzyrządowanie. Jedną z nich jest geometria dziewięciu punktów, gdzie bez linijki czy cyrkla można "konstruować" całkiem dokładnie koła, trójkąty i inne figury.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W zawodach stopnia pierwszego wzięło udział 13299 uczniów z 1221 szkół, do zawodów stopnia drugiego zakwalifikowano 1151 uczniów z 501 szkół, a do zawodów stopnia trzeciego - 194 uczniów z 99 szkół.

W zawodach stopnia pierwszego wzięło udział 1171 uczniów, do zawodów stopnia drugiego zakwalifikowano 617 uczniów, a do zawodów stopnia trzeciego - 113 uczniów.

Wywiad z prof. dr Andrzejem Białynickim-Birulą.

Co to znaczy udowodnić twierdzenie matematycznej Logicy dawno już odpowiedzieli na to pytanie, podając definicję dowodu formalnego jako ciągu zdań kończącego się dowodzonym twierdzeniem i o tej własności, że następne zdanie ciągu powstaje z poprzedniego w myśl prostych, ustalonych reguł.

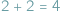Słyszy się często: "to pewne, jak ". Zdania matematyczne bywają podawane za wzór niewzruszonej i absolutnej prawdy. Pytanie, jakie zdania? Niewątpliwie pewniki, czyli aksjomaty ("przez dwa punkty przechodzi dokładnie jedna prosta") oraz twierdzenia, choćby tak łatwe, jak to zacytowane na początku.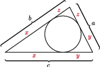

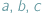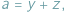
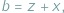
Jeśli w nierówności, którą chcemy uzasadnić, występują długości boków pewnego trójkąta, często przydaje się podstawienie Raviego: 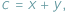gdzie 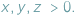Takie liczby 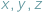zawsze istnieją, są to bowiem długości odcinków stycznych do okręgu wpisanego w trójkąt.

Euklides w Elementach pisał: "... kwadrat jest tym, co równoboczne i prostokątne...". Oto kilka niebanalnych obserwacji, w których kwadrat jest jednym z bohaterów.

Powiada Ewangelia: Łatwiej jest wielbłądowi przejść przez ucho igielne, niż bogatemu wejść do królestwa niebieskiego.

Matematyka Poglądowa stanowi kontynuację zeszytów Matematyka-Społeczeństwo-Nauczanie, które towarzyszyły Szkołom Matematyki Poglądowej od samego początku (od ponad ćwierć wieku). Artykuły to zazwyczaj relacje z odczytów na Szkołach, ale nie tylko. Można tam również znaleźć recenzje książek (rzecz jasna, poświęconych matematyce) oraz różne perełki, jak, na przykład, wykład habilitacyjny Riemanna, którego pierwsze polskie tłumaczenie ukazało się właśnie w MSN.

Czym jest Cykada 3301? Jest to tajemnicza organizacja, która trzykrotnie (w roku 2012, 2013, 2014) dała o sobie znać, publikując w Internecie cykle ukrytych łamigłówek. Zostały one okrzyknięte przez Washington Post "najbardziej skomplikowanymi i tajemniczymi zagadkami w dobie Internetu".

Na stole leżą, ułożone w losowej kolejności koszulkami do góry, trzy karty: As, Król i Dama. Jeżeli gracz odgadnie prawidłowo położenie Asa, wygrywa dużą nagrodę. Gracz wskazał kartę, nie obejrzał jej, i wtedy prowadzący grę mówi: Chwileczkę. Odkryję jedną z dwóch pozostałych kart, a ty się zastanów, czy chcesz zmienić swoją kartę na kartę, która pozostała nieodkryta.

Czym jest Bitcoin? Najkrótsza odpowiedź na to pytanie brzmi: kryptowalutą. Ale nie w takim sensie krypto-, jak w słowie kryptoreklama. Pierwszy człon tego terminu pochodzi od kryptologii, czyli nauki kojarzącej nam się głównie z szyframi i maszyną szyfrującą Enigma używaną przez Niemców podczas wojny. To właśnie twierdzenia i konstrukcje z tej dziedziny stoją za funkcjonowaniem i bezpieczeństwem Bitcoina.

Jak już pisałem (Delta 3/1979), metodę dedukcyjną i jej najdoskonalszą postać - metodę aksjomatyczną można wyprowadzić ze zwykłej praktyki dyskusji, niezmiernie rozpowszechnionych w starożytnej Grecji. Warto zobaczyć, co o strukturze pierwszego znanego nam aksjomatycznego wykładu matematyki -- Elementów Euklidesa może nam powiedzieć taka interpretacja.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W wielu zadaniach należy uzasadnić, że pewne trzy proste przecinają się w jednym punkcie. Często można wykazać, że wszystkie one są symetralnymi, dwusiecznymi, wysokościami albo środkowymi pewnego trójkąta, co oczywiście kończy dowód.

Chyba każdy patrzył kiedyś w kalejdoskop - prostokątne lustra odbijające różnobarwne wzory powstałe z przesypujących się koralików. Nie znam nikogo, kto mając w ręku owo urządzenie, byłby w stanie powstrzymać się przed choćby najmniejszym obróceniem nim i zerknięciem przez małe oczko na otrzymany efekt. A gdyby odwrócić sytuację i zbadać, jak zmieni się obraz, gdy zamiast koralikami poruszymy lustrami znajdującymi się w kalejdoskopie? Zacznijmy od wyprawy do szklarza i wyboru bohatera kalejdoskopowych przygód - po starannym castingu wygrywa żaba.

Piętnastego marca stracona została rubież intelektualnej przewagi człowieka nad sztuczną inteligencją, za jaką była uznawana maestria gry w Go. Zakończyła się ostatnia, piąta partia między AlphaGo, programem firmy DeepMind (będącej własnością Google) i Lee Se-dolem (9 dan - najwyższy stopień wtajemniczenia), jednym z najlepszych, jeżeli nie najlepszym zawodowym graczem. AlphaGo wygrał pierwsze trzy rozgrywki. Lee Se-dol wygrał czwartą i, po niezwykle zaciętej walce, przegrał ostatnią.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Rzucamy monetą. Jeśli wypadnie orzeł - wygrywam ja, jeśli reszka - wygrywa mój przeciwnik. Czy jest to gra sprawiedliwa? Uważam, że tak. A oto inna gra. Rzucamy kostką do gry. Jeśli wypadnie szóstka - wygrywa mój przeciwnik, jeśli co innego - wygrywam ja. W moim odczuciu ta gra jest niesprawiedliwa, niekorzystna dla mojego przeciwnika. Czy zgadzacie się ze mną? Jeśli tak, to w porządku, rozumiemy się doskonale...

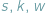W 1752 roku znakomity matematyk szwajcarski Euler, podówczas profesor Akademii Nauk w Berlinie, odkrył zadziwiający związek między liczbami ścian, krawędzi i wierzchołków dowolnego wielościanu wypukłego 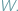Związek ten jest obecnie nazywany wzorem Eulera dla wielościanów i zwykle zapisuje się go w postaci

Podamy elementarny i chyba nader zabawny dowód tego wzoru.

Na rynku w Babilonie dwóch kupców, Nabonit i Enkidu, sprzedawało swoje towary. Łączyła ich wielka przyjaźń, ale też przy lada okazji lubili się sprzeczać i kłócić. Ostatnio powstał między nimi spór o sposób ważenia towarów...

Lecz wy się uczcie patrzeć, a nie gapić - B. Brecht