Delta mi!

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Na początek stwierdzenie: w nauce, a zwłaszcza w matematyce, zajmujemy się tylko wyjątkowymi, wyidealizowanymi sytuacjami.

W rozwiązaniach wielu zadań kluczowe jest rozłożenie danej bryły tak, by uzyskać jej siatkę. Jeśli z kolei chcemy zbudować model wielościanu, często rysujemy jego siatkę, wycinamy, składamy... Siatki to przydatne narzędzie, jednakże - jak to z narzędziami bywa - trzeba ostrożnie się nimi posługiwać. Proszę ocenić poprawność poniższych trzech stwierdzeń.

25. kwietnia odbyły się finałowe zawody jubileuszowej, X Olimpiady Matematycznej Gimnazjalistów, a dzień później, 26. kwietnia w pięknej auli Politechniki Warszawskiej 86. uczestnikom wręczono dyplomy laureatów.

Matematyka bardzo się w XIX wieku zmieniła. Algebra, badająca dotąd przede wszystkim metody rozwiązywania równań wielomianowych, dzięki pracom Evariste'a Galois, George'a Boole'a i innych wytworzyła struktury abstrakcyjne: grupy, pierścienie, algebry Boole'a, oderwane od obliczeń liczbowych, reprezentujące za to pewne ogólne własności działań (na dowolnych obiektach). Geometria utraciła euklidesową jednoznaczność, odnajdując się w światach dotąd nieznanych i nieprzewidywanych, zwanych geometriami nieeuklidesowymi. Analiza, nabierając coraz bardziej potrzebnej ścisłości, wyszła poza granice intuicji, uwzględniając szerszy repertuar funkcji (niegdyś uważanych za ciągłe z definicji) i dopuszczając zaskakujące konstrukcje, jak choćby funkcje wszędzie ciągłe i nigdzie nieróżniczkowalne.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

W zawodach stopnia pierwszego wzięło udział 895 uczniów, do zawodów stopnia drugiego zakwalifikowano 409 uczniów, a do zawodów stopnia trzeciego - 126 uczniów.

Artykuł Modelowanie fikcji: inwazja zombie miał za zadanie przypomnieć, że zastosowania matematyki nie są ograniczone ramami świata rzeczywistego (a przynajmniej takiego, jaki za rzeczywisty w danym momencie uważamy). Dzięki uniwersalności matematyki potrafimy modelować wszystko, co tylko możemy sobie wyobrazić: w szczególności to, co powstało w umysłach twórców literatury i filmów science-fiction. Poniżej zaprezentuję przykład wykorzystania metod matematycznych (dokładniej, statystycznych) do rozwiązania problemów postawionych przed bohaterami popularnego serialu Battlestar Galactica.

We współczesnej nauce obserwuje się dynamiczny rozwój nauk interdyscyplinarnych. Wśród nich można wymienić badania nad sztucznymi sieciami neuronowymi, które są modelami matematycznymi projektowanymi w celu przetwarzania informacji i mają zastosowanie w wielu dziedzinach nauki. Modele te są inspirowane występującymi w naturze strukturami neuronalnymi, takimi jak, na przykład, ludzki mózg. Ze względu na biologiczne inspiracje zagadnienia związane z sieciami neuronowymi najwygodniej omawiać, zakładając, że mają charakterystyczne cechy zbliżone do naturalnych struktur neuronowych.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Dylemat społeczny to sytuacja grupy ludzi, w której interes jednostki nie jest zbieżny z interesem grupy - występuje konflikt między interesem prywatnym a zbiorowym. Charakteryzuje się tym, że jeżeli członkowie grupy postąpią zgodnie ze swoimi indywidualnymi interesami, to zyskają mniej, niż gdyby brali przede wszystkim pod uwagę w swoich działaniach interes grupy. Jeżeli jednak wszyscy mieliby postąpić zgodnie z interesem grupy, to osoba, która jako jedyna zmieni decyzję i postąpi zgodnie ze swoim indywidualnym interesem, zyska więcej, niż gdyby działała zgodnie z interesem grupy.

W wielu zadaniach występują różnokolorowe punkty płaszczyzny, a w ich rozwiązaniach przydatne bywają rozmaite rozumowania kombinatoryczne.

Jaką długość ma linia śrubowa owijająca dwukrotnie walec o promieniu 1 i wysokości 4, tak jak widać na obrazku? Oczywiście, 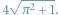Aby przekonać się, że rzeczywiście, wystarczy spojrzeć na obrazek z prawej - jeśli nawiniemy go na walec, to otrzymamy obrazek z lewej.

Z czym kojarzy się Monte Carlo? Z kasynami, hazardem, ruletką. A więc Monte Carlo jest symbolem potęgi przypadku, który jednym pozwala zbijać fortuny, innych rujnuje. Są jednak ludzie, którzy przypadkowość, losowość potrafią okiełznać i wykorzystać z pożytkiem (przynajmniej dla siebie). Oczywiście, takimi ludźmi są właściciele kasyn gry, ale nie tylko. Również matematycy zaprzęgają losowość do pożytecznej roboty. Metody obliczeniowe oparte na generowaniu (symulowaniu komputerowym) zdarzeń losowych nazywają się... oczywiście, metodami Monte Carlo.

Czego można się nauczyć, studiując na Wydziale Matematyki, Informatyki i Mechaniki UW?
Odpowiedź krótka: wszystkiego tego, co można sformułować precyzyjnie w języku matematyki, czyli wszystkiego.
Odpowiedź praktyczna: tego, czym się zajmują nasi pracownicy - kilka przykładów przedstawimy w tym i następnych artykułach.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Czy jest coś weselszego na twarzy drugiego człowieka od jego uśmiechu? To w pewnym sensie filozoficzne pytanie potrafi wzbudzić wiele zainteresowania u każdego człowieka. Wszak każda osoba posiada swój własny kanon piękna oraz szczęścia...

W geometrii rzutowej przyjmujemy, że każde dwie proste równoległe przecinają się w pewnym ustalonym punkcie w nieskończoności, odpowiadającym ich kierunkowi, oraz że wszystkie takie punkty w nieskończoności tworzą prostą ("horyzont"). Poniżej przedstawiamy przykłady pojęć i twierdzeń rzutowych oraz ich zastosowań; dopuszczamy w nich takie właśnie punkty przecięcia "na horyzoncie".

W LXVI Olimpiadzie Matematycznej wzięło udział 895 uczniów, więc aż o 272 osoby mniej niż w pierwszym stopniu poprzedniej Olimpiady. Niżej podpisanemu, który nie jest w tym osądzie osamotniony, wydaje się, że jest to związane z trudnością zadań, których rozwiązanie zaproponowaliśmy uczestnikom bieżącej OM.

Dawno, dawno temu za górami, za lasami na Euklidesowych Równinach żyło sobie koło. Niezmiernie było dumne ze swej stałej szerokości. Chadzało ścieżkami, które miały szerokość równą jego średnicy, i jako jedyna figura zamieszkująca równiny mogło kręcić się przy tym jak szalone, stale podpierając obie krawędzie ścieżki.

W pierwszej części cyklu (Delta 2/2015) mieliśmy okazję przyjrzeć się wybranym przykładom zaskakujących połączeń, z którymi możemy spotkać się w świecie matematyki. W drugiej części zapoznamy się z jednym z takich połączeń dużo dokładniej. Mowa tu o metodzie probabilistycznej, wiązanej często z nazwiskiem Paula Erdősa, który w trakcie swojej kariery naukowej korzystał z niej niezliczoną liczbę razy.

Podczas XXVII Kongresu Matematycznego, odbywającego się w Seulu między 13 a 21 sierpnia 2014 roku, prestiżową Nagrodę Nevanlinny (informatyczny odpowiednik Medalu Fieldsa) otrzymał pracujący w USA hinduski informatyk Subhash Khot. W laudacji poświęconej wynikom Khota jego mentor i współautor wielu prac, Sanjeev Arora, wspomniał o przełomowym wyniku uzyskanym przez profesora Uniwersytetu Warszawskiego, Krzysztofa Oleszkiewicza wraz z Elchananem Mosselem i Ryanem O'Donnellem...

W dniach 24-26 października 2014 roku odbyła się kolejna - siódma już - konferencja organizowana przez Stowarzyszenie na rzecz Edukacji Matematycznej. Konferencja była okazją do spotkania się osób z różnych środowisk zaangażowanych w edukację matematyczną, popularyzację matematyki i pracę z młodzieżą uzdolnioną matematycznie.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty