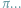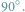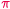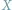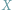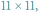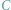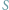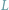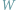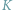Czy
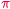 jest constans?
jest constans?
Jedną z najistotniejszych wielkości w matematyce jest
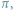 której poświęcono
wiele ścisłych prac i filozoficznych rozważań od starożytności (jeszcze zanim
została nazwana swoim obecnym imieniem) do czasów współczesnych. Co pewien
czas można znaleźć informacje o kolejnych rekordach w wyznaczaniu coraz
dłuższego jej rozwinięcia dziesiętnego. Przeglądając literaturę, portale o tematyce
matematycznej bądź podręczniki szkolne, można także spotkać się z różnymi
sposobami definiowania liczby
której poświęcono
wiele ścisłych prac i filozoficznych rozważań od starożytności (jeszcze zanim
została nazwana swoim obecnym imieniem) do czasów współczesnych. Co pewien
czas można znaleźć informacje o kolejnych rekordach w wyznaczaniu coraz
dłuższego jej rozwinięcia dziesiętnego. Przeglądając literaturę, portale o tematyce
matematycznej bądź podręczniki szkolne, można także spotkać się z różnymi
sposobami definiowania liczby