Diagramy Venna
W tym artykule zajmiemy się nieco dokładniej diagramami Venna.
Diagramy Venna były tematem znakomitego artykułu „Pizza Venna” w
Delcie 03/2004.
Najpierw powiemy, co to jest niezależna rodzina zbiorów.
Przypuśćmy, że mamy daną rodzinę
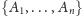 podzbiorów
pewnego ustalonego zbioru
podzbiorów
pewnego ustalonego zbioru
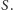 Od tej pory wszystkie rozpatrywane
zbiory będą podzbiorami tego zbioru
Od tej pory wszystkie rozpatrywane
zbiory będą podzbiorami tego zbioru
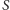 (będziemy go nazywać
przestrzenią
(będziemy go nazywać
przestrzenią
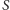 ). Niech
). Niech
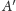 oznacza dopełnienie zbioru
oznacza dopełnienie zbioru
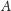 do przestrzeni
do przestrzeni
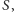 tzn.
tzn.
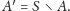 Oznaczmy następnie
Oznaczmy następnie
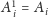 oraz
oraz
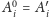 dla
dla
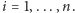 Każdy zbiór postaci
Każdy zbiór postaci
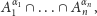 gdzie
gdzie
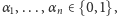 nazywamy składową
rodziny
nazywamy składową
rodziny
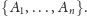 Oczywiście każda
Oczywiście każda
 -elementowa
rodzina zbiorów ma
-elementowa
rodzina zbiorów ma
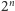 składowych. Składowymi rodziny zbiorów
składowych. Składowymi rodziny zbiorów
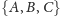 będą zbiory:
będą zbiory:

Gdy wszystkie składowe rodziny
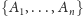 są różne i niepuste,
rodzinę nazwiemy niezależną.
są różne i niepuste,
rodzinę nazwiemy niezależną.
A oto przykład rodziny niezależnej
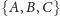 podzbiorów przestrzeni
podzbiorów przestrzeni
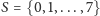 :
:

Rodziny niezależne są wykorzystywane w dowodach tożsamości z rachunku zbiorów. Prawdziwe jest bowiem następujące twierdzenie.
Twierdzenie. Niech
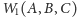 i
i
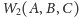 będą wyrażeniami rachunku zbiorów tzn. występują
w nich tylko zbiory
będą wyrażeniami rachunku zbiorów tzn. występują
w nich tylko zbiory
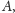
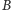 i
i
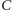 oraz symbole działań
na zbiorach:
oraz symbole działań
na zbiorach:
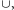
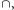
 . Jeśli dla pewnej niezależnej
rodziny
. Jeśli dla pewnej niezależnej
rodziny
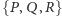 podzbiorów pewnej przestrzeni
podzbiorów pewnej przestrzeni
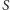 zachodzi
równość
zachodzi
równość
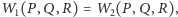 to ta równość zachodzi
także dla dowolnych zbiorów
to ta równość zachodzi
także dla dowolnych zbiorów
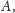
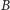 i
i
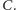
Twierdzenia tego nie będziemy dowodzić, popatrzymy natomiast na przykład jego
zastosowania. Udowodnimy równość
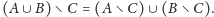 Dla naszej rodziny niezależnej mamy:
Dla naszej rodziny niezależnej mamy:

Okazało się, że dla tej rodziny niezależnej zachodzi dowodzona
równość. Zatem ta równość jest prawdziwa dla dowolnych zbiorów
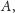
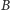 i
i
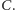 Podobne twierdzenie jest prawdziwe dla wyrażeń
zawierających więcej zbiorów. Dowód znajduje się np. w książce.
Podobne twierdzenie jest prawdziwe dla wyrażeń
zawierających więcej zbiorów. Dowód znajduje się np. w książce.
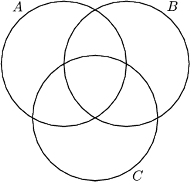
Rys. 1
Dowody takie jak powyższy szczególnie łatwo przeprowadzić na rysunku.
Rysujemy niezależną rodzinę podzbiorów pewnej przestrzeni
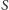 i zaznaczamy na tym rysunku zbiory występujące po obu stronach równości.
Jeśli oba zaznaczone zbiory są identyczne, to równość zachodzi dla
dowolnych zbiorów. Niezależną rodzinę zbiorów
i zaznaczamy na tym rysunku zbiory występujące po obu stronach równości.
Jeśli oba zaznaczone zbiory są identyczne, to równość zachodzi dla
dowolnych zbiorów. Niezależną rodzinę zbiorów
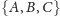 najprościej
narysować w następujący sposób.
najprościej
narysować w następujący sposób.
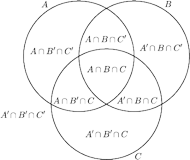
Rys. 2
Taki rysunek nazywamy diagramem Venna. Każdy z
 zbiorów naszej
rodziny niezależnej
zbiorów naszej
rodziny niezależnej
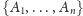 jest narysowany w postaci pewnego
podzbioru płaszczyzny (w naszym przypadku są to trzy koła), przy czym
rozważana przestrzeń (u nas płaszczyzna) jest podzielona krzywymi
ograniczającymi zbiory
jest narysowany w postaci pewnego
podzbioru płaszczyzny (w naszym przypadku są to trzy koła), przy czym
rozważana przestrzeń (u nas płaszczyzna) jest podzielona krzywymi
ograniczającymi zbiory
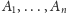 na
na
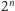 (u nas
(u nas
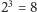 )
części. Każda z tych części odpowiada jednej składowej (zakładamy, że
części te są spójne, czyli w jednym kawałku).
)
części. Każda z tych części odpowiada jednej składowej (zakładamy, że
części te są spójne, czyli w jednym kawałku).
W dalszym ciągu ustalimy jednolity sposób numerowania składowych. Numerem składowej

jest liczba, której kolejnymi cyframi w zapisie w systemie dwójkowym
są:
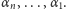 Na przykład, jeśli naszą rodziną niezależną jest
Na przykład, jeśli naszą rodziną niezależną jest
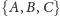 (tzn.
(tzn.
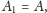
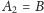 oraz
oraz
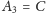 ), to
składowa
), to
składowa

ma numer 6, gdyż liczba 6 ma zapis dwójkowy 110. Podobnie składowa

ma numer 3, gdyż liczba 3 ma zapis dwójkowy 11, czyli inaczej 011.
W przypadku, gdy rodzina niezależna składa się z czterech zbiorów
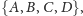 to składowa
to składowa

ma numer 10, gdyż liczba 10 ma zapis dwójkowy 1010.
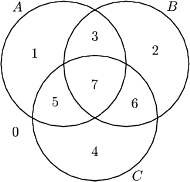
Rys. 3
Na rysunku obok pokazany jest nasz diagram Venna dla trzech zbiorów
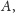
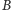 i
i
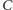 ze składowymi ponumerowanymi w ten
sposób.
ze składowymi ponumerowanymi w ten
sposób.
Czytelnik zechce sam sprawdzić, że zbiory po obu stronach równości

wyglądają tak, jak na Rys. 4.
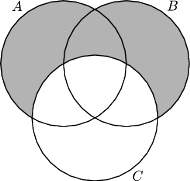
Rys. 4
Rys. 5
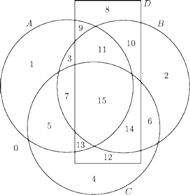
Rys. 6
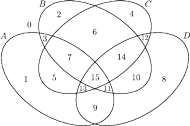
Rys. 7
Z powyższych rozważań widać, że umiejętność rysowania niezależnych
rodzin zbiorów (czyli diagramów Venna) może się przydać w praktyce
do dowodzenia równości w rachunku zbiorów. We wspomnianym artykule
została pokazana jedna metoda rysowania diagramów Venna. Jednak diagramy
dla dużych liczb
 były bardzo skomplikowane i mało czytelne. Powstaje
naturalne pytanie, czy można narysować diagram Venna, w którym wszystkie
zbiory mają stosunkowo prostą postać. Diagram Venna dla trzech zbiorów
można było narysować za pomocą trzech okręgów. A czy można
tak narysować cztery okręgi, by tworzyły diagram Venna dla czterech
zbiorów?
były bardzo skomplikowane i mało czytelne. Powstaje
naturalne pytanie, czy można narysować diagram Venna, w którym wszystkie
zbiory mają stosunkowo prostą postać. Diagram Venna dla trzech zbiorów
można było narysować za pomocą trzech okręgów. A czy można
tak narysować cztery okręgi, by tworzyły diagram Venna dla czterech
zbiorów?
Okazuje się, że jest to niemożliwe. Mianowicie za pomocą trzech okręgów
można podzielić płaszczyznę na co najwyżej 8 części. Czwarty okrąg
przetnie każdy z dotychczasowych okręgów w co najwyżej dwóch
punktach; te punkty podzielą go zatem na co najwyżej 6 łuków. Każdy łuk
dzieli jeden obszar na dwie części. Zatem cztery okręgi dzielą płaszczyznę
na co najwyżej
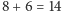 części. Nie otrzymamy zatem diagramu
Venna, gdyż taki diagram dla czterech zbiorów ma mieć 16 składowych.
Rozumując w podobny sposób, można pokazać, że jeśli
części. Nie otrzymamy zatem diagramu
Venna, gdyż taki diagram dla czterech zbiorów ma mieć 16 składowych.
Rozumując w podobny sposób, można pokazać, że jeśli
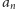 oznacza maksymalną liczbę części, na jakie
oznacza maksymalną liczbę części, na jakie
 okręgów może
podzielić płaszczyznę, to ciąg
okręgów może
podzielić płaszczyznę, to ciąg
 spełnia następujące równania
rekurencyjne:
spełnia następujące równania
rekurencyjne:

Nietrudno teraz dowieść przez indukcję, że
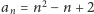 ; dla
; dla
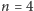 otrzymamy
otrzymamy
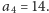 Zatem żadna konfiguracja czterech
okręgów na płaszczyźnie nie tworzy diagramu Venna. Oczywiście, czwarty
zbiór możemy dorysować do trzech okręgów inaczej
Zatem żadna konfiguracja czterech
okręgów na płaszczyźnie nie tworzy diagramu Venna. Oczywiście, czwarty
zbiór możemy dorysować do trzech okręgów inaczej
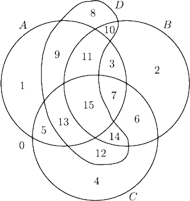
Na rysunku 5. mamy przykład takich czterech zbiorów.
Składowe na tym diagramie Venna zostały ponumerowane zgodnie z przyjętą wyżej zasadą. Powstaje oczywiście pytanie, czy można dorysować czwarty zbiór tak, by był on zbiorem wypukłym. Gdy byłem jeszcze studentem, wydawało mi się to oczywiście niemożliwe; zresztą tak uważało wielu moich kolegów. Rysunek 6, który mimo wszystko kiedyś udało mi się narysować, wprawił mnie w zrozumiałe zdumienie.
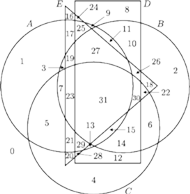
Rys. 8
Inny diagram Venna otrzymamy, rysując cztery elipsy.
Jeszcze inny, składający się z czterech prostokątów, można łatwo narysować samemu. Prostokąty te mają wierzchołki w punktach o następujących współrzędnych:

Gdy udało się narysować diagram Venna, w którym wszystkie cztery zbiory były wypukłe, należało spróbować zrobić to samo dla pięciu zbiorów. Do trzech kół i prostokąta udało mi się dorysować jeszcze trójkąt.
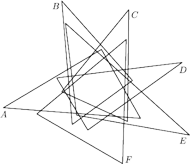
Rys. 9 Można również narysować diagram Venna składający się z pięciu trójkątów.

Rys. 10 Szczególnie ładny jest utworzony na podobnej zasadzie diagram Venna złożony z pięciu elips.
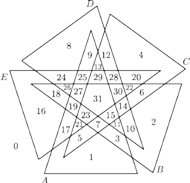
Rys. 11 Można także narysować diagram Venna składający się z sześciu trójkątów. elips.
Wierzchołki trójkątów z rysunku 11 mają następujące współrzędne

Okazuje się jednak, że nie można narysować diagramu Venna złożonego
z więcej niż sześciu trójkątów. Aby tego dowieść, pokażemy najpierw,
że jeśli
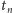 jest największą liczbą obszarów, na jakie
jest największą liczbą obszarów, na jakie
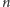 trójkątów może podzielić płaszczyznę, to ciąg
trójkątów może podzielić płaszczyznę, to ciąg
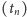 spełnia następujące
równania rekurencyjne:
spełnia następujące
równania rekurencyjne:
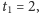
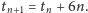 Jeden trójkąt
oczywiście dzieli płaszczyznę na dwa obszary. Przypuśćmy teraz, że mamy
już
Jeden trójkąt
oczywiście dzieli płaszczyznę na dwa obszary. Przypuśćmy teraz, że mamy
już
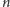 trójkątów na płaszczyźnie. Następny trójkąt przecina
każdy z tych
trójkątów na płaszczyźnie. Następny trójkąt przecina
każdy z tych
 trójkątów w co najwyżej 6 punktach. Te punkty
przecięcia dzielą obwód tego ostatniego trójkąta na co najwyżej
trójkątów w co najwyżej 6 punktach. Te punkty
przecięcia dzielą obwód tego ostatniego trójkąta na co najwyżej
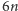 części; każda z tych części dzieli jeden obszar na dwie części. Zatem
maksymalna liczba części, na jakie możemy podzielić płaszczyznę za pomocą
części; każda z tych części dzieli jeden obszar na dwie części. Zatem
maksymalna liczba części, na jakie możemy podzielić płaszczyznę za pomocą
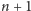 trójkątów, wynosi co najwyżej
trójkątów, wynosi co najwyżej
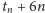 (pozostawimy jako
ćwiczenie przekonanie się, że można tak umieścić
(pozostawimy jako
ćwiczenie przekonanie się, że można tak umieścić
 trójkątów
na płaszczyźnie, by każde dwa przecinały się w dokładnie 6 punktach;
taka konfiguracja da właśnie
trójkątów
na płaszczyźnie, by każde dwa przecinały się w dokładnie 6 punktach;
taka konfiguracja da właśnie
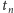 części). Teraz można łatwo
udowodnić przez indukcję, że
części). Teraz można łatwo
udowodnić przez indukcję, że
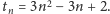 Można również
łatwo udowodnić, że jeśli
Można również
łatwo udowodnić, że jeśli
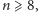 to
to
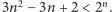 To
pokazuje, że jeśli
To
pokazuje, że jeśli
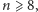 to żadna konfiguracja
to żadna konfiguracja
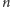 trójkątów
na płaszczyźnie nie tworzy diagramu Venna. Jeśli zaś
trójkątów
na płaszczyźnie nie tworzy diagramu Venna. Jeśli zaś
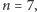 to
to
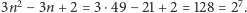 Zatem można tak umieścić 7
trójkątów na płaszczyźnie, by podzieliły one płaszczyznę na
Zatem można tak umieścić 7
trójkątów na płaszczyźnie, by podzieliły one płaszczyznę na
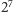 obszarów. Jednak taka konfiguracja nie będzie diagramem Venna. Mianowicie
każde dwa trójkąty muszą przecinać się w sześciu punktach, a więc
wierzchołki każdego trójkąta leżą na zewnątrz każdego innego. Stąd wynika,
że w każdym trójkącie trzy obszary wewnętrzne, na których brzegu leżą
wierzchołki, zawarte są tylko w tym jednym trójkącie, a więc stanowią części
tej samej składowej. A to znaczy, że ta konfiguracja nie jest diagramem
Venna.
obszarów. Jednak taka konfiguracja nie będzie diagramem Venna. Mianowicie
każde dwa trójkąty muszą przecinać się w sześciu punktach, a więc
wierzchołki każdego trójkąta leżą na zewnątrz każdego innego. Stąd wynika,
że w każdym trójkącie trzy obszary wewnętrzne, na których brzegu leżą
wierzchołki, zawarte są tylko w tym jednym trójkącie, a więc stanowią części
tej samej składowej. A to znaczy, że ta konfiguracja nie jest diagramem
Venna.
Widzimy więc, że istnieje diagram Venna złożony z sześciu trójkątów i nie
istnieją diagramy Venna złożone z
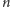 trójkątów dla
trójkątów dla
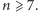 A jak
jest z czworokątami wypukłymi? Albo z pięciokątami wypukłymi? A czy
dla każdego
A jak
jest z czworokątami wypukłymi? Albo z pięciokątami wypukłymi? A czy
dla każdego
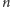 istnieje diagram Venna złożony z wielokątów
wypukłych? Odpowiedzi na niektóre tak postawione pytania są znane. Myślę
jednak, że można spróbować na podobne pytania odpowiedzieć
samemu. W książce znajduje się obszerny przegląd wiadomości na temat
diagramów Venna. Są tam też odnośniki do wielu innych interesujących
źródeł.
istnieje diagram Venna złożony z wielokątów
wypukłych? Odpowiedzi na niektóre tak postawione pytania są znane. Myślę
jednak, że można spróbować na podobne pytania odpowiedzieć
samemu. W książce znajduje się obszerny przegląd wiadomości na temat
diagramów Venna. Są tam też odnośniki do wielu innych interesujących
źródeł.