Delta mi!

Suma kwadratów najczęściej kojarzy się nam z twierdzeniem Pitagorasa - słusznie, ale warto wiedzieć, że temat ten ma swoje miejsce również w teorii liczb, gdzie interesuje nas, czy daną liczbę całkowitą można przedstawić w postaci sumy kwadratów innych liczb całkowitych. Intrygujące jest również pytanie, ile składników znajduje się w tej sumie. Osiągnięcia w tym zakresie mieli między innymi Fermat, Euler i Lagrange...

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

O wyrażeniach symetrycznych oraz uproszczeniach, które można stosować w rozwiązywaniu zadań z takimi wyrażeniami.

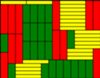
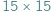W autorskim tygodniku internetowym Trapez Jarosław Wróblewski proponuje serię zadań (nr 75-126) o parkietowaniu prostokątów. Na przykład: czy planszę da się szczelnie pokryć klockami o wymiarach 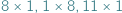oraz 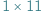(oczywiście klocki nie mogą na siebie zachodzić).

Ence-pence w której ręce? - za moich dziecięcych lat przedstawiona formułka, której towarzyszyły często dwie wyciągnięte przez wypowiadającą ją osobę ręce, była zwiastunem jakiejś bardzo przyjemnej (najczęściej słodkiej) niespodzianki. Każda wyciągnięta dłoń skrywała bowiem coś dobrego, jednak jako szkrab i tak poświęcałem chwilę zastanowienia nad jej wyborem, będąc świadomym ryzyka, że niewskazana przeze mnie ręka zawiera bardziej atrakcyjny podarek i powędruje on do mojego brata.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Niniejszy odcinek Deltoidu o okrągłym (w systemie jedenastkowym) numerze jest odcinkiem ostatnim. Nie kryjemy smutku z tego powodu, cieszymy się jednocześnie, że na naszych łamach ta wspaniała seria ukazywała się przez okrągłych 10 lat. Mamy nadzieję, że jeszcze wiele razy nazwisko Autorki zagości w naszym spisie treści.
Joasiu, za Twoją nienaganną punktualność w dostarczaniu materiałów, zegarmistrzowską dokładność przy ich korekcie, a przede wszystkim za deltoidową fantastyczność serdecznie dziękujemy!

Redakcja

Powiążemy tu wzór Leibniza

z geometrią (pola) i teorią liczb. Tekst jest wyraźnie dłuższy od tego, który jest w książce Hilberta i Cohn-Vossena, bo szkicujemy dowód twierdzenia z teorii liczb, na które autorzy jedynie powołują się. Pozostawimy jednak bez dowodu niektóre bardzo znane twierdzenia z teorii liczb, ze względu na ograniczenia miejsca w miesięczniku. 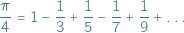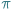Zaznaczyć warto, że podawany zwykle studentom pierwszego roku dowód jest krótszy, ale zdaniem autora tego tekstu, nie pokazuje związku z geometrią, który jest mocno sugerowany obecnością we wzorze.

Na nieskończoność natrafiono już w starożytności. Nic dziwnego, że była traktowana z podejrzliwością, w końcu wszystko w prawdziwym świecie wydawało się skończone. Bywała źródłem problemów, paradoksów i sporów (na przykład, paradoks Zenona z Elei). W końcu, w drugiej połowie XIX wieku, nieskończoność udało się nieco oswoić (nie mylić z ujarzmić), weszła do kanonu matematyki, a właściwie w jej fundamenty. Owo oswajanie zaczęło się od Georga Cantora...

Nieskończoność... Co myślisz, gdy słyszysz to słowo? Może myślisz o rozgwieżdżonym niebie? Może próbujesz wyobrazić sobie coś bardzo, ale to bardzo dużego? A może myślisz o ludzkiej wyobraźni i sile naszego umysłu? George Cantor postanowił potraktować nieskończoność jak coś "zwykłego" i po prostu ją zbadał. Pójdziemy jego śladem. Zastanówmy się... Czy każda nieskończoność jest taka sama? Czy też może są większe i mniejsze? Czy wszechświat jest nieskończony? Co to jest nieskończoność? Na wiele pytań dotyczących nieskończoności udzielono wyczerpujących odpowiedzi. Na część z nich odpowiedzi nie są znane. O niektórych wiadomo, że nie da się na nie odpowiedzieć po prostu "tak" lub "nie".

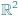Na płaszczyźnie euklidesowej zbiór 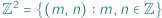nazywamy kratą, a jego elementy punktami kratowymi.

Bywa tak, że chcemy o czymś przekonać niedowiarków, jednak w taki sposób, aby uwierzyli, ale też aby za dużo się nie dowiedzieli. Fabularna, nieinformatyczna ilustracja, którą lubię przywoływać, gdy próbuję wyrazić, o co mi chodzi, jest następująca. Wyobraźmy sobie, że potrafię zliczyć liczbę liści na drzewie, jeśli tylko spojrzę na nie przez 5 sekund. Więcej: twierdzę, że umiem to publicznie udowodnić w przeciągu 5 minut, i to tak, że wszyscy mi uwierzą, ale nikt się nie zorientuje, jak ja to robię!

Nieoczywiste zastosowania oczywistego stwierdzenia: pomiędzy dwiema kolejnymi liczbami całkowitymi nie ma żadnej liczby całkowitej.

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Począwszy od Pitagorasa wierzymy, że przyroda działa zgodnie z regułami matematyki. Wobec tego odszukajmy reguły, którymi kierował się siódmaczek (Trientalis) z naszych zagajników, wybierając siedmiokrotną symetrię swoich kwiatów.

Większości problemów otwartych współczesnej matematyki nie da się zrozumieć bez zaawansowanej wiedzy, ale zdarzają się też takie, których sformułowania są zupełnie elementarne. Poniższa seria zadań prowadzi do jednego z nich.

Na torze w kształcie okręgu o obwodzie jednostkowym ściga się kolarzy. Każdy pędzi z inną, ale stałą prędkością. Wystartowali z tego samego punktu, jadą w tym samym kierunku. Jest ciemno, nic nie widać, choć oko wykol...

Wyobraźmy sobie porowaty materiał, może to być gleba, a może to być... ubita kawa w kawiarce. Czy przez ten materiał można przesączyć wodę? Intuicyjnie wiemy, że jest to możliwe w przypadku kawy, ale już w przypadku gleby zależy od jej rodzaju, a dokładniej - od struktury "porów wolnej przestrzeni". W roku 1957 matematycy angielscy, Simon Broadbent i John Hammersley, zaproponowali probabilistyczny model opisujący materiały porowate. Pomimo prostoty definicji model ten (zwany perkolacjami) okazał się fascynującym tematem badań. Wspomnijmy, że, między innymi, za wyniki dotyczące perkolacji Stanisław Smirnow został nagrodzony w 2010 roku najwyższym matematycznym wyróżnieniem, Medalem Fieldsa.

Teoria Gier (TG), traktowana jako dział matematyki, służy do wyjaśniania zachowań ludzi, zwierząt, przebiegu różnorodnych procesów w przyrodzie, ekonomii, medycynie, zachowania podmiotów w polityce, w sieciach społecznych, czyli - ogólniej - służy do opisu interakcji między różnego typu obiektami. Procesy te są na tyle złożone, że istniejące modele teoriogrowe nie przystają na ogół do obserwowanych sytuacji. Przykładem jest równowaga Nasha, która stanowi matematyczny opis stabilnego układu. Jednak w rzeczywistych sytuacjach ludzie nieczęsto grają strategiami tworzącymi taką równowagę.

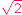
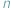Niech będzie liczbą nieparzystą...

Spójrzmy na dwa grafy na poniższym rysunku. Wyglądają zupełnie inaczej, prawda?

Liga zadaniowa Wydziału Matematyki, Informatyki i Mechaniki, Wydziału Fizyki Uniwersytetu Warszawskiego i Redakcji Delty

Zapewne każdy z czytających te słowa grał kiedyś w marynarza, ale na wypadek gdyby któryś z Czytelników miał smutne dzieciństwo pozbawione tej gry, pokrótce wyjaśnię zasady: na ustalony sygnał każdy z uczestników przedstawia wybraną przez siebie liczbę (najczęściej przy użyciu własnych palców). Następnie rozpoczyna się (cykliczne) wyliczanie uczestników aż do sumy przedstawionych przez nich liczb (oczywiście, należy zawczasu ustalić, od kogo rozpoczyna się wyliczanka). Osoba, na której zakończy się wyliczanie, jest "zwycięzcą" (wziętym w cudzysłów, gdyż "nagrodą" może być, na przykład, zmywanie naczyń)...

Podzielmy kostkę na 27 przystających sześcianów (jak w kostce Rubika), a następnie wyrzućmy 7 z nich: ten ze środka oraz środkowy na każdej ze ścian. W kolejnych krokach konstrukcji powtarzajmy powyższą operację dla każdego z pozostających mniejszych sześcianów.